Estimate a spectral density function

The objective of this example is to estimate the spectral density function from data, which can be a sample of time series or one time series.

The following example illustrates the case where the available data is a sample of realizations of the process, defined on the time grid , discretized every . The spectral model of the process is the Cauchy model parameterized by and .

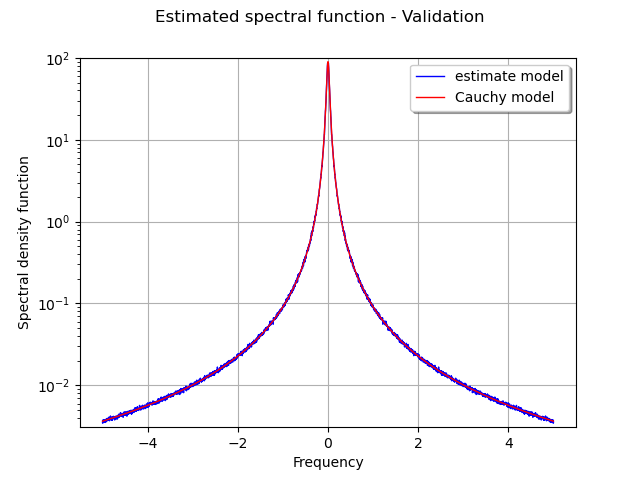
The figure draws the graph of the real spectral model and its estimation from the sample of time series.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

generate some data

# Create the time grid
# In the context of the spectral estimate or Fourier transform use,
# we use data blocs with size of form 2^p
tMin = 0.0
tstep = 0.1
size = 2**12
tgrid = ot.RegularGrid(tMin, tstep, size)

# We fix the parameter of the Cauchy model
amplitude = [5.0]
scale = [3.0]
model = ot.CauchyModel(amplitude, scale)
process = ot.SpectralGaussianProcess(model, tgrid)

# Get a time series or a sample of time series
tseries = process.getRealization()
sample = process.getSample(1000)

Build a spectral model factory

segmentNumber = 10
overlapSize = 0.3
factory = ot.WelchFactory(ot.Hann(), segmentNumber, overlapSize)

Estimation on a TimeSeries or on a ProcessSample

estimatedModel_TS = factory.build(tseries)
estimatedModel_PS = factory.build(sample)

Change the filtering window

factory.setFilteringWindows(ot.Hamming())

Get the frequencyGrid

frequencyGrid = ot.SpectralGaussianProcess(estimatedModel_PS, tgrid).getFrequencyGrid()

# With the model, we want to compare values
# We compare values computed with theoritical values
plotSample = ot.Sample(frequencyGrid.getN(), 3)

# Loop of comparison ==> data are saved in plotSample
for k in range(frequencyGrid.getN()):
    freq = frequencyGrid.getStart() + k * frequencyGrid.getStep()
    plotSample[k, 0] = freq
    plotSample[k, 1] = abs(estimatedModel_PS(freq)[0, 0])
    plotSample[k, 2] = abs(model(freq)[0, 0])

# Some cosmetics : labels, legend position, ...
graph = ot.Graph(
    "Estimated spectral function - Validation",
    "Frequency",
    "Spectral density function",
    True,
    "topright",
    1.0,
    ot.GraphImplementation.LOGY,
)

# The first curve is the estimate density as function of frequency
curve1 = ot.Curve(plotSample.getMarginal([0, 1]))
curve1.setColor("blue")
curve1.setLegend("estimate model")

# The second curve is the theoritical density as function of frequency
curve2 = ot.Curve(plotSample.getMarginal([0, 2]))
curve2.setColor("red")
curve2.setLegend("Cauchy model")

graph.add(curve1)
graph.add(curve2)
view = viewer.View(graph)
plt.show()