Optimization with constraints

In this example we are going to expose methods to solve a generic optimization problem in the form

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

define the objective function

objective = ot.SymbolicFunction(
    ["x1", "x2", "x3", "x4"], ["x1 + 2 * x2 - 3 * x3 + 4 * x4"]
)

define the constraints

inequality_constraint = ot.SymbolicFunction(["x1", "x2", "x3", "x4"], ["x1-x3"])

define the problem bounds

dim = objective.getInputDimension()
bounds = ot.Interval([-3.0] * dim, [5.0] * dim)

define the problem

problem = ot.OptimizationProblem(objective)
problem.setMinimization(True)
problem.setInequalityConstraint(inequality_constraint)
problem.setBounds(bounds)

solve the problem

algo = ot.Cobyla()
algo.setProblem(problem)
startingPoint = [0.0] * dim
algo.setStartingPoint(startingPoint)
algo.run()

retrieve results

result = algo.getResult()
print("x^=", result.getOptimalPoint())

x^= [5,-3,5,-3]

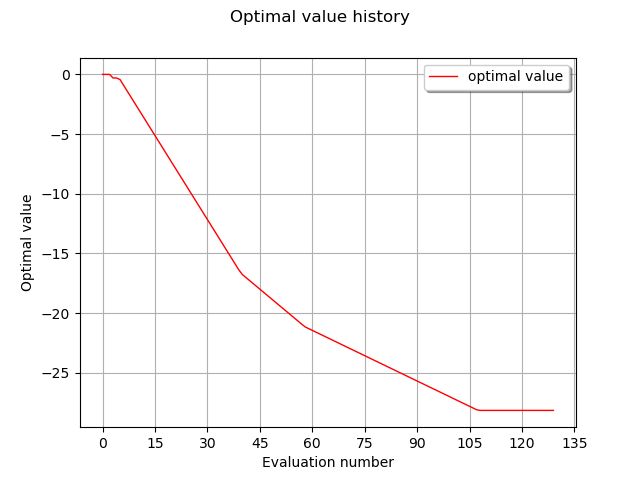
draw optimal value history

graph = result.drawOptimalValueHistory()
view = viewer.View(graph)
plt.show()