Note
Go to the end to download the full example code
Create and draw scalar distributions¶
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)
A continuous distribution¶
We build a normal distribution with parameters :
distribution = ot.Normal(2.2, 0.6)
print(distribution)
Normal(mu = 2.2, sigma = 0.6)
We can draw a sample following this distribution with the getSample method :
size = 10
sample = distribution.getSample(size)
print(sample)
[ X0 ]
0 : [ 2.90698 ]
1 : [ 2.4694 ]
2 : [ 2.37417 ]
3 : [ 2.69831 ]
4 : [ 2.28606 ]
5 : [ 2.08412 ]
6 : [ 2.87742 ]
7 : [ 1.80004 ]
8 : [ 1.67943 ]
9 : [ 2.99115 ]
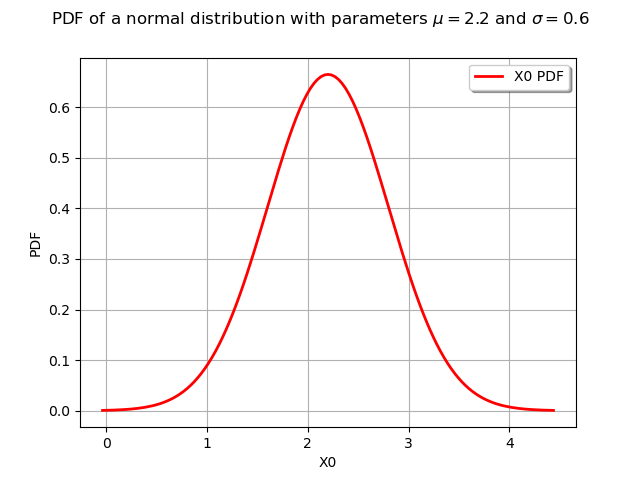
We draw its PDF and CDF :
graphPDF = distribution.drawPDF()
graphPDF.setTitle(
r"PDF of a normal distribution with parameters $\mu = 2.2$ and $\sigma = 0.6$"
)
view = viewer.View(graphPDF)
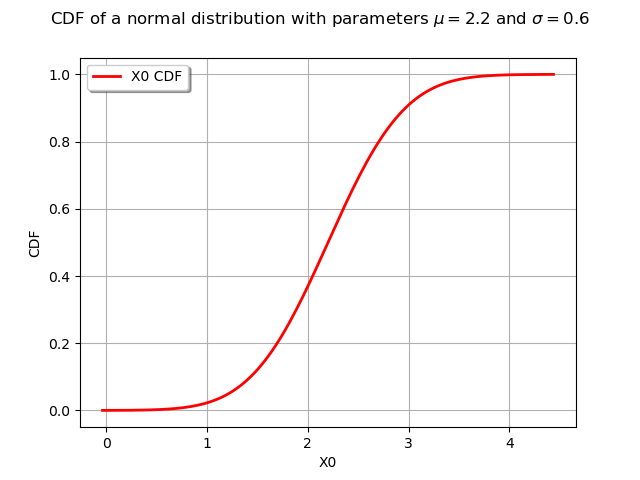
graphCDF = distribution.drawCDF()
graphCDF.setTitle(
r"CDF of a normal distribution with parameters $\mu = 2.2$ and $\sigma = 0.6$"
)
view = viewer.View(graphCDF)
A discrete distribution¶
We define a geometric distribution with parameter .
p = 0.7
distribution = ot.Geometric(p)
print(distribution)
Geometric(p = 0.7)
We draw a sample of it :
size = 10
sample = distribution.getSample(size)
print(sample)
[ X0 ]
0 : [ 3 ]
1 : [ 1 ]
2 : [ 1 ]
3 : [ 2 ]
4 : [ 1 ]
5 : [ 2 ]
6 : [ 1 ]
7 : [ 1 ]
8 : [ 1 ]
9 : [ 2 ]
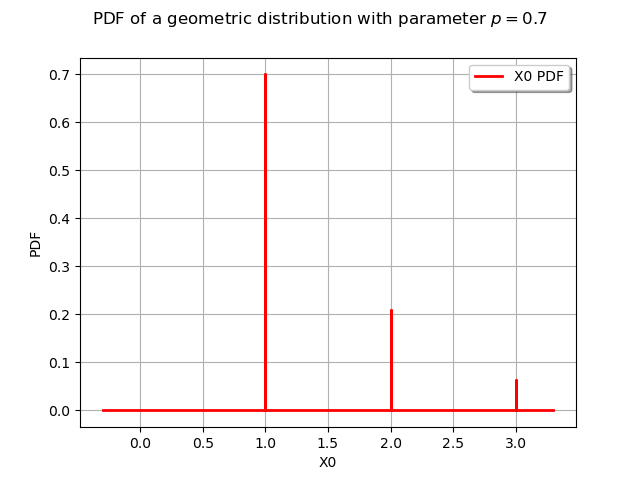
We draw its PDF and its CDF :
graphPDF = distribution.drawPDF()
graphPDF.setTitle(r"PDF of a geometric distribution with parameter $p = 0.7$")
view = viewer.View(graphPDF)
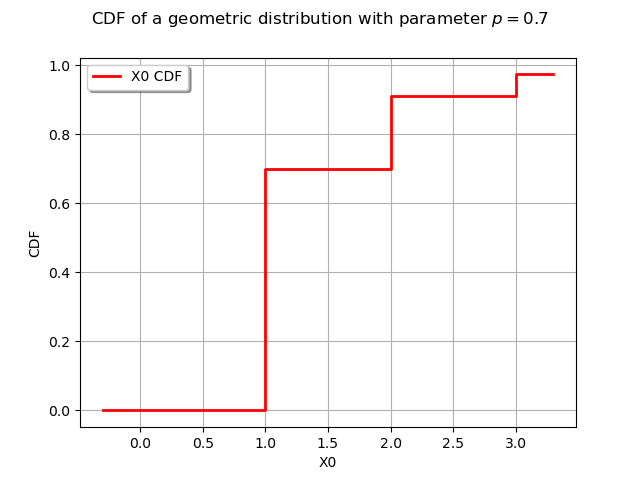
graphCDF = distribution.drawCDF()
graphCDF.setTitle(r"CDF of a geometric distribution with parameter $p = 0.7$")
view = viewer.View(graphCDF)
Conclusion¶
The two previous examples look very similar despite their continuous and discrete nature. In the library there is no distinction between continuous and discrete distributions.
Display all figures
plt.show()
Total running time of the script: ( 0 minutes 0.270 seconds)
 OpenTURNS
OpenTURNS