Graphical goodness-of-fit tests

This method deals with the modelling of a probability distribution of a random vector \vect{X} = \left( X^1,\ldots,X^{n_X} \right). It seeks to verify the compatibility between a sample of data \left\{ \vect{x}_1,\vect{x}_2,\ldots,\vect{x}_N \right\} and a candidate probability distribution previous chosen. The use of graphical tools allows one to answer this question in the one dimensional case n_X =1, and with a continuous distribution. The QQ-plot, and henry line tests are defined in the case to n_X = 1. Thus we denote \vect{X} = X^1 = X. The first graphical tool provided is a QQ-plot (where “QQ” stands for “quantile-quantile”). In the specific case of a Normal distribution, Henry’s line may also be used.

QQ-plot

A QQ-Plot is based on the notion of quantile. The \alpha-quantile q_{X}(\alpha) of X, where \alpha \in (0, 1), is defined as follows:

\begin{aligned} \Prob{ X \leq q_{X}(\alpha)} = \alpha \end{aligned}

If a sample \left\{x_1,\ldots,x_N \right\} of X is available, the quantile can be estimated empirically:

  1. the sample \left\{x_1,\ldots,x_N \right\} is first placed in ascending order, which gives the sample \left\{ x_{(1)},\ldots,x_{(N)} \right\};

  2. then, an estimate of the \alpha-quantile is:

    \begin{aligned} \widehat{q}_{X}(\alpha) = x_{([N\alpha]+1)} \end{aligned}

where [N\alpha] denotes the integral part of N\alpha.

Thus, the j^\textrm{th} smallest value of the sample x_{(j)} is an estimate \widehat{q}_{X}(\alpha) of the \alpha-quantile where \alpha = (j-1)/N (1 < j \leq N).

Let us then consider the candidate probability distribution being tested, and let us denote by F its cumulative distribution function. An estimate of the \alpha-quantile can be also computed from F:

\begin{aligned} \widehat{q}'_{X}(\alpha) = F^{-1} \left( (j-1)/N \right) \end{aligned}

If F is really the cumulative distribution function of F, then \widehat{q}_{X}(\alpha) and \widehat{q}'_{X}(\alpha) should be close. Thus, graphically, the points \left\{ \left( \widehat{q}_{X}(\alpha),\widehat{q}'_{X}(\alpha)\right),\ \alpha = (j-1)/N,\ 1 < j \leq N \right\} should be close to the diagonal.

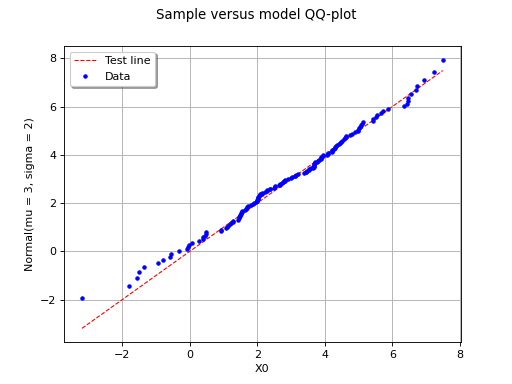
The following figure illustrates the principle of a QQ-plot with a sample of size N=50. Note that the unit of the two axis is that of the variable X studied; the quantiles determined via F are called here “value of T”. In this example, the points remain close to the diagonal and the hypothesis “F is the cumulative distribution function of X” does not seem irrelevant, even if a more quantitative analysis (see for instance ) should be carried out to confirm this.

(Source code, png, hires.png, pdf)

../../_images/graphical_fitting_test-1.png

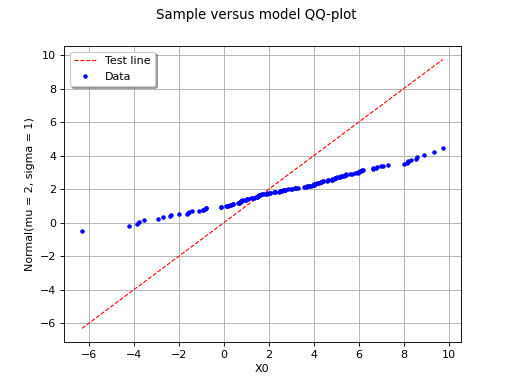
In this second example, the candidate distribution function is clearly irrelevant.

(Source code, png, hires.png, pdf)

../../_images/graphical_fitting_test-2.png

Henry’s line

This second graphical tool is only relevant if the candidate distribution function being tested is gaussian. It also uses the ordered sample \left\{ x_{(1)},\ldots,x_{(N)} \right\} introduced for the QQ-plot, and the empirical cumulative distribution function \widehat{F}_N presented in .

By definition,

\begin{aligned} x_{(j)} = \widehat{F}_N^{-1} \left( \frac{j}{N} \right) \end{aligned}

Then, let us denote by \Phi the cumulative distribution function of a Normal distribution with mean 0 and standard deviation 1. The quantity t_{(j)} is defined as follows:

\begin{aligned} t_{(j)} = \Phi^{-1} \left( \frac{j}{N} \right) \end{aligned}

If X is distributed according to a normal probability distribution with mean \mu and standard-deviation \sigma, then the points \left\{ \left( x_{(j)},t_{(j)} \right),\ 1 \leq j \leq N \right\} should be close to the line defined by t = (x-\mu) / \sigma. This comes from a property of a normal distribution: it the distribution of X is really \cN(\mu,\sigma), then the distribution of (X-\mu) / \sigma is \cN(0,1).

The following figure illustrates the principle of Henry’s graphical test with a sample of size N=50. Note that only the unit of the horizontal axis is that of the variable X studied. In this example, the points remain close to a line and the hypothesis “the distribution function of X is a Gaussian one” does not seem irrelevant, even if a more quantitative analysis (see for instance ) should be carried out to confirm this.

(Source code, png, hires.png, pdf)

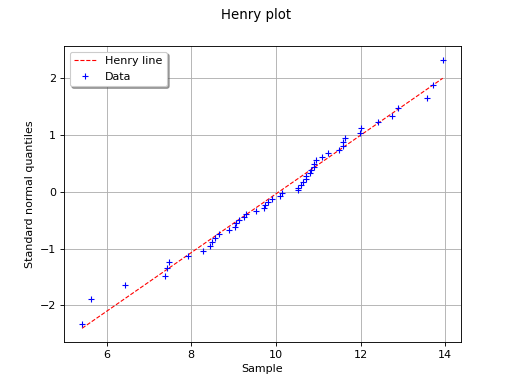
../../_images/graphical_fitting_test-3.png

In this example the test validates the hypothesis of a gaussian distribution.

(Source code, png, hires.png, pdf)

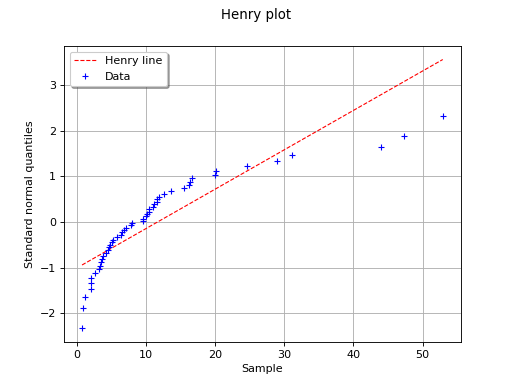
../../_images/graphical_fitting_test-4.png

In this second example, the hypothesis of a gaussian distribution seems far less relevant because of the behavior for small values of X.

Kendall plot

In the bivariate case, the Kendall Plot test enables to validate the choice of a specific copula model or to verify that two samples share the same copula model.

Let \vect{X} be a bivariate random vector which copula is noted C. Let (\vect{X}^i)_{1 \leq i \leq N} be a sample of \vect{X}.

We note:

\begin{aligned} \forall i \geq 1, \displaystyle H_i = \frac{1}{n-1} Card \left\{ j \in [1,N], j \neq i, \, | \, x^j_1 \leq x^i_1 \mbox{ and } x^j_2 \leq x^i_2 \right \} \end{aligned}

and (H_{(1)}, \dots, H_{(N)}) the ordered statistics of (H_1, \dots, H_N).

The statistic W_i is defined by:

(1)W_i = N C_{N-1}^{i-1} \int_0^1 t K_0(t)^{i-1} (1-K_0(t))^{n-i} \, dK_0(t)

where K_0(t) is the cumulative density function of H_i. We can show that this is the cumulative density function of the random variate C(U,V) when U and V are independent and follow Uniform(0,1) distributions.

Equation (1) is evaluated with the Monte Carlo sampling method : it generates n samples of size N from the bivariate copula C, in order to have n realizations of the statistics H_{(i)},\forall 1 \leq i \leq N and have an estimation of W_i = E[H_{(i)}], \forall i \leq N.
When testing a specific copula with respect to a sample, the Kendall Plot test draws the points (W_i, H_{(i)})_{1 \leq i \leq N}. If the points are one the first diagonal, the copula model is validated.
When testing whether two samples have the same copula, the Kendall Plot test draws the points (H^1_{(i)}, H^2_{(i)})_{1 \leq i \leq N} respectively associated to the first and second sample. Note that the two samples must have the same size.

(Source code, png, hires.png, pdf)

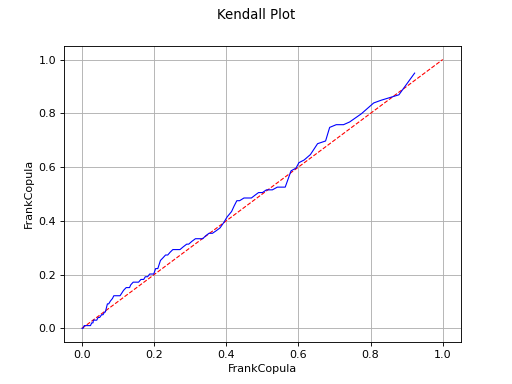
../../_images/graphical_fitting_test-5.png

The Kendall Plot test validates the use of the Frank copula for a sample.

(Source code, png, hires.png, pdf)

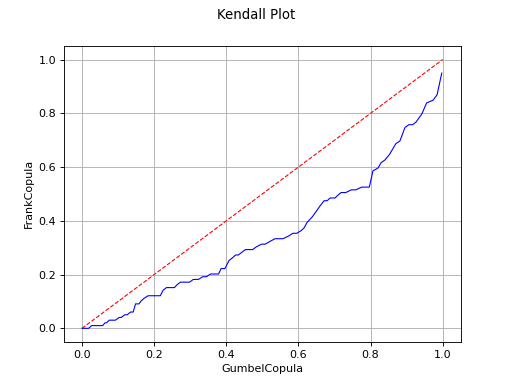
../../_images/graphical_fitting_test-6.png

The Kendall Plot test invalidates the use of the Frank copula for a sample.

Remark: In the case where you want to test a sample with respect to a specific copula, if the size of the sample is superior to 500, we recommend to use the second form of the Kendall plot test: generate a sample of the proper size from your copula and then test both samples. This way of doing is more efficient.