Strong Maximum Test¶

The Strong Maximum Test is used under the following context: $\vect{X}$ denotes a random input vector, representing the sources of uncertainties, $\pdf$ its joint density probability, $\vect{d}$ a deterministic vector, representing the fixed variables $g(\vect{X}\,,\,\vect{d})$ the limit state function of the model, $\cD_f = \{\vect{X} \in \Rset^n \, / \, g(\vect{X}\,,\,\vect{d}) \le 0\}$ the event considered here and ${g(\vect{X}\,,\,\vect{d}) = 0}$ its boundary (also called limit state surface).

The probability content of the event $\cD_f$ :

(1)¶ $\begin{aligned} P_f &=& \int_{{g(\vect{X}\,,\,\vect{d}) \le 0}} \pdf\, d\vect{x}. \end{aligned}$

may be evaluated with the FORM or SORM method.

In order to evaluate an approximation of , these analytical
methods uses the Nataf isoprobabilistic transformation which maps the
probabilistic model in terms of  onto an equivalent
model in terms of  independent standard normal random
 (refer to to have details on the transformation). In
that new -space, the event has the new expression
defined from the transformed limit state function of the model
 :

and its boundary:
.
These analytical methods rely on the assumption that most of the
contribution to  comes from points located in the vicinity
of a particular point , the design point, defined in the
-space as the point located on the limit state surface
and of maximal likelihood. Given the probabilistic characteristics of
the -space,  has a geometrical
interpretation : it is the point located on the event boundary and at
minimal distance from the center of the -space. Thus,
the design point  is the result of a constrained
optimization problem.
The FORM/SORM methods suppose that  is unique.
One important difficulty comes from the fact that numerical method
involved in the determination of  gives no guaranty of a
global optimum : the point to which it converges might be a local
optimum only. In that case, the contribution of the points in the
vicinity of the real design point is not taken into account, and this
contribution is the most important one.
Furthermore, even in the case where the global optimum has really been
found, there may exist another local optimum  which
likelihood is slightly inferior to the design point one, which means
its distance from the center of the -space is slightly
superior to the design point one. Thus, points in the vicinity of
 may contribute significantly to the probability
 and are not taken into account in the FORM and SORM
approximations.
In these both cases, the FORM and SORM approximations are of bad
quality because they neglect important contributions to  .
The Strong Maximum Test helps to evaluate the quality of the design
point resulting from the optimization algorithm. It checks whether the
design point computed is:

the true design point, which means a global maximum point,
a strong design point, which means that there is no other local maximum located on the event boundary and which likelihood is slightly inferior to the design point one.

This verification is very important in order to give sense to the FORM and SORM approximations.

The principle of the Strong Maximum Test relies on the geometrical definition
of the design point.
The objective is to detect all the points  in the
ball of radius 
which are potentially the real design point (case of
) or which contribution to  is not
negligible as regards the approximations Form and SORM (case of
). The contribution of a point is considered as
negligible when its likelihood in the -space is more
than -times lesser than the design point one. The
radius  is the distance to the
-space center upon which points are considered as
negligible in the evaluation of .
In order to catch the potential points located on the sphere of radius
 (frontier of the zone of prospection), it is
necessary to go a little further more : that’s why the test samples
the sphere of radius ,
with .
Points on the sampled sphere which are in the vicinity of the design
point  are less interesting than those verifying the event
and located far from the design point : these last ones might reveal
a potential  which contribution to  has
to be taken into account. The vicinity of the design point is defined
with the angular parameter  as the cone centered on
 and of half-angle .
The number  of the simulations sampling the sphere of radius
 is determined to ensure that the test detect with a
probability greater than  any point verifying the event
and outside the design point vicinity.

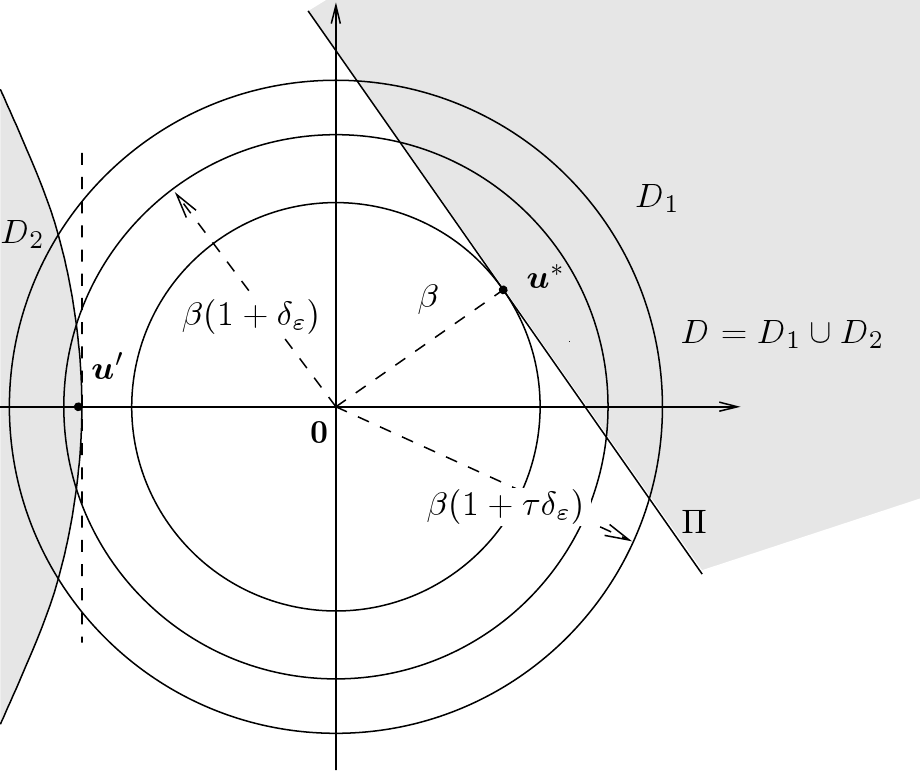
The vicinity of the Design Point is the arc of the sampled sphere which is inside the half space which frontier is the linearized limit state function at the Design Point: the vicinity is the arc included in the half space $D_1$ .

../../_images/StrongMaxTest_vicinity.png

The Strong Maximum Test proceeds as follows. The User selects the parameters:

the importance level $\varepsilon$ , where $0 < \varepsilon < 1$ ,
the accuracy level $\tau$ , where $\tau >0$ ,
the confidence level $(1 - q)$ where $0<q<1$ or the number of points $N$ used to sample the sphere. The parameters are deductible from one other.

The Strong Maximum Test will sample the sphere of radius $\beta(1+\tau \delta_{\varepsilon})$ , where $\delta_{\varepsilon} = \sqrt{1 - 2 \frac{\ln(\varepsilon)}{\beta^2}}- 1$ .

The test will detect with a probability greater than $(1 - q)$ any point of $\cD_f$ which contribution to $P_f$ is not negligible (i.e. which density value in the $\vect{u}$ -space is greater than $\varepsilon$ times the density value at the design point).

The Strong Maximum Test provides:

set 1: all the points detected on the sampled sphere that are in $\cD_f$ and outside the design point vicinity, with the corresponding value of the limit state function,
set 2: all the points detected on the sampled sphere that are in $\cD_f$ and in the design point vicinity, with the corresponding value of the limit state function,
set 3: all the points detected on the sampled sphere that are outside $\cD_f$ and outside the design point vicinity, with the corresponding value of the limit state function,
set 4: all the points detected on the sampled sphere that are outside $\cD_f$ but in the vicinity of the design point, with the corresponding value of the limit state function.

Points are described by their coordinates in the $\vect{x}$ -space.

The parameter  is directly linked to the hypothesis
according to which the boundary of the space  is supposed
to be well approximated by a plane near the design point, which is
primordial for a FORM approximation of the probability content of
. Increasing  is increasing the area where
the approximation FORM is applied.
The parameter  also serves as a measure of distance from
the design point  for a hypothetical local maximum:
the greater it is, the further we search for another local maximum.
Numerical experiments show that it is recommended to take
 (see the given reference below).
The following table helps to quantify the parameters of the test for a
problem of dimension 5.

$\beta_g$	$\varepsilon$	$\tau$	$1-q$	$\delta_{\varepsilon}$	$N$
3.0	0.01	2.0	0.9	$4.224 e^{-1}$	62
3.0	0.01	2.0	0.99	$4.224 e^{-1}$	124
3.0	0.01	4.0	0.9	$4.224 e^{-1}$	15
3.0	0.01	4.0	0.99	$4.224 e^{-1}$	30
3.0	0.1	2.0	0.9	$2.295 e^{-1}$	130
3.0	0.1	2.0	0.99	$2.295 e^{-1}$	260
3.0	0.1	4.0	0.9	$2.295 e^{-1}$	26
3.0	0.1	4.0	0.99	$2.295 e^{-1}$	52
5.0	0.01	2.0	0.9	$1.698 e^{-1}$	198
5.0	0.01	2.0	0.99	$1.698 e^{-1}$	397
5.0	0.01	4.0	0.9	$1.698 e^{-1}$	36
5.0	0.01	4.0	0.99	$1.698 e^{-1}$	72
5.0	0.1	2.0	0.9	$8.821 e^{-2}$	559
5.0	0.1	2.0	0.99	$8.821 e^{-2}$	1118
5.0	0.1	4.0	0.9	$8.821 e^{-2}$	85
5.0	0.1	4.0	0.99	$8.821 e^{-2}$	169

$\beta_g$	$\varepsilon$	$\tau$	$N$	$\delta_{\varepsilon}$	$1-q$
3.0	0.01	2.0	100	$4.224e^{-1}$	0.97
3.0	0.01	2.0	1000	$4.224e^{-1}$	1.0
3.0	0.01	4.0	100	$4.224e^{-1}$	1.0
3.0	0.01	4.0	1000	$4.224e^{-1}$	1.0
3.0	0.1	2.0	100	$2.295e^{-1}$	0.83
3.0	0.1	2.0	1000	$2.295e^{-1}$	1.0
3.0	0.1	4.0	100	$2.295e^{-1}$	1.0
3.0	0.1	4.0	1000	$2.295e^{-1}$	1.0
5.0	0.01	2.0	100	$1.698e^{-1}$	0.69
5.0	0.01	2.0	1000	$1.698e^{-1}$	1.0
5.0	0.01	4.0	100	$1.698e^{-1}$	1.0
5.0	0.01	4.0	1000	$1.698e^{-1}$	1.0
5.0	0.1	2.0	100	$8.821 e^{-2}$	0.34
5.0	0.1	2.0	1000	$8.821 e^{-2}$	0.98
5.0	0.1	4.0	100	$8.821 e^{-2}$	0.93
5.0	0.1	4.0	1000	$8.821 e^{-2}$	0.99

As the Strong Maximum Test involves the computation of $N$ values of the limit state function, which is computationally intensive, it is interesting to have more than just an indication about the quality of $\vect{OP}^*$ . In fact, the test gives some information about the trace of the limit state function on the sphere of radius $\beta(1+\tau \delta_{\varepsilon})$ centered on the origin of the $\vect{u}$ -space. Two cases can be distinguished:

Case 1: set 1 is empty. We are confident on the fact that $\vect{OP}^*$ is a design point verifying the hypothesis according to which most of the contribution of $P_f$ is concentrated in the vicinity of $\vect{OP}^*$ . By using the value of the limit state function on the sample $(\vect{U}_1, \dots, \vect{U}_N)$ , we can check if the limit state function is reasonably linear in the vicinity of $\vect{OP}^*$ , which can validate the second hypothesis of FORM.

If the behavior of the limit state function is not linear, we can decide to use an importance sampling version of the Monte Carlo method for computing the probability of failure. However, the information obtained through the Strong Max Test, according to which $\vect{OP}^*$ is the actual design point, is quite essential : it allows one to construct an effective importance sampling density, e.g. a multidimensional Gaussian distribution centered on $\vect{OP}^*$ .
Case 2: set 1 is not empty. There are two possibilities:
1. We have found some points that suggest that $\vect{OP}^*$ is not a strong maximum, because for some points of the sampled sphere, the value taken by the limit state function is slightly negative;
2. We have found some points that suggest that $\vect{OP}^*$ is not even the global maximum, because for some points of the sampled sphere, the value taken by the limit state function is very negative.
  
  In the first case, we can decide to use an importance sampling version of the Monte Carlo method for computing the probability of failure, but with a mixture of e.g. multidimensional gaussian distributions centered on the $U_i$ in $\cD_f$ (refer to ). In the second case, we can restart the search of the design point by starting at the detected $U_i$ .

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

Strong Maximum Test¶