FejerAlgorithm¶

(Source code, png, hires.png, pdf)

class FejerAlgorithm(*args)¶

Fejer Integration algorithm

Available constructors:

FejerAlgorithm(dimension=1, method=FejerAlgorithm.FEJERTYPE1)

FejerAlgorithm(discretization, method=FejerAlgorithmFEJERTYPE1)

Parameters:

dimensionint, $dimension>0$

The dimension of the functions to integrate. The default discretization is FejerAlgorithm-DefaultMarginalIntegrationPointsNumber in each dimension, see ResourceMap.

discretizationsequence of int

The number of nodes in each dimension. The sequence must be non-empty and must contain only positive values.

methodint, optional

Integer used to select the method of integration. (Amongst ot.FejerAlgorithm.FEJERTYPE1, ot.FejerAlgorithm.FEJERTYPE2 and ot.FejerAlgorithm.CLENSHAWCURTIS).

Default is ot.FejerAlgorithm.FEJERTYPE1

Notes

The FejerAlgorithm algorithm enables to approximate the definite integral:

$\int_{\vect{a}}^\vect{b} f(\vect{t})\di{\vect{t}}$

with $f: \Rset^d \mapsto \Rset^p$ , $\vect{a}, \vect{b}\in\Rset^d$ using a the approximation:

$\int_{\vect{a}}^\vect{b} f(\vect{t})\di{\vect{t}} = \sum_{\vect{n}\in \cN}\left(\prod_{i=1}^d w^{N_i}_{n_i}\right)f(\xi^{N_1}_{n_1},\dots,\xi^{N_d}_{n_d})$

where $\xi^{N_i}_{n_i}$ is the $n_i`th node of the :math:`N_i$ -points and $w^{N_i}_{n_i}$ the associated weight.

Let us note $\theta_k=\dfrac{k\pi}{n}, k=0,1,...,n-1$ , $x_k = cos(\theta_k)$ . The Clenshaw-Curtis nodes are $x_k$ and its associated weights are given as follows:

$w_k =\dfrac{c_k}{n}\left(1-\sum_{j=1}^{\lfloor n/2\rfloor}\dfrac{b_j}{4j^2-1}\cos\left(2j\theta_k\right)\right)$

with $b_j= 2$ if $j < n/2$ else $b_j=1$ . Also, $c_k = 1$ if $if k = 0[n]$ else $c_k = 2$

The type-1 Fejer quadrature rule relies on $x_k = cos(\theta_{k+1/2})$ nodes and associated weights are the following:

$w_k=\dfrac{2}{n}\left(1-2\sum_{j=1}^{\lfloor n/2\rfloor}\dfrac{1}{4j^2-1}\cos\left(j\theta_{2k+1}\right)\right)$

Finally, the type-2 Fejer quadrature rule is very close to the Clenshaw-Curtis one. The two method do share the same nodes (except the endpoints that are set to 0 within the Fejer method). Its associated weights are given as follows:

$w_k=\dfrac{4}{n+1}\sin\theta_k\sum_{j=1}^{\lfloor n/2\rfloor}\dfrac{\sin\left((2j-1)\theta_k\right)}{2j-1}$

Examples

Create a FejerAlgorithm algorithm:

>>> import openturns as ot
>>> algo = ot.FejerAlgorithm(2)
>>> algo = ot.FejerAlgorithm([2, 4, 5])

Methods

`getClassName`()	Accessor to the object's name.
`getDiscretization`()	Accessor to the discretization of the tensorized rule.
`getId`()	Accessor to the object's id.
`getName`()	Accessor to the object's name.
`getNodes`()	Accessor to the integration nodes.
`getShadowedId`()	Accessor to the object's shadowed id.
`getVisibility`()	Accessor to the object's visibility state.
`getWeights`()	Accessor to the integration weights.
`hasName`()	Test if the object is named.
`hasVisibleName`()	Test if the object has a distinguishable name.
`integrate`(*args)	Evaluation of the integral of $f$ on an interval.
`setName`(name)	Accessor to the object's name.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setVisibility`(visible)	Accessor to the object's visibility state.

integrateWithNodes

__init__(*args)¶

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDiscretization()¶

Accessor to the discretization of the tensorized rule.

Returns:

discretizationIndices: The number of integration point in each dimension.

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getNodes()¶

Accessor to the integration nodes.

Returns:

nodesSample: The tensorized FejerAlgorithm integration nodes on $[0,1]^d$ where $d>0$ is the dimension of the integration algorithm.

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

getWeights()¶

Accessor to the integration weights.

Returns:

weightsPoint: The tensorized FejerAlgorithm integration weights on $[0,1]^d$ where $d>0$ is the dimension of the integration algorithm.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

integrate(*args)¶

Evaluation of the integral of $f$ on an interval.

Available usages:

integrate(f, interval)

integrate(f, interval, xi)

Parameters:

fFunction, $f: \Rset^d \mapsto \Rset^p$: The integrand function.
intervalInterval, $interval \in \Rset^d$: The integration domain.
xiSample: The integration nodes.

Returns:

valuePoint: Approximation of the integral.

Examples

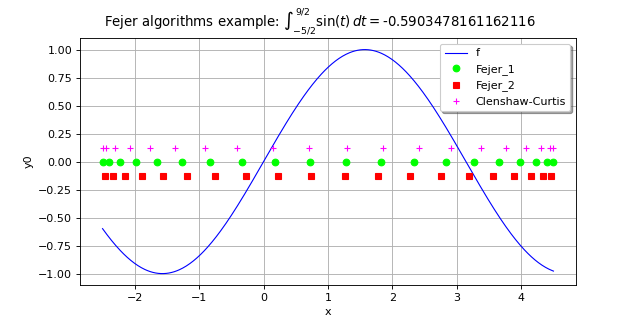
>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x'], ['sin(x)'])
>>> a = -2.5
>>> b = 4.5
>>> algoF1 = ot.FejerAlgorithm([10])
>>> value = algoF1.integrate(f, ot.Interval(a, b))[0]
>>> print(value)
-0.590...

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters:

idint: Internal unique identifier.

setVisibility(visible)¶

Accessor to the object’s visibility state.

Parameters:

visiblebool: Visibility flag.

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

FejerAlgorithm¶