QuantileMatchingFactory¶

class QuantileMatchingFactory(*args)¶

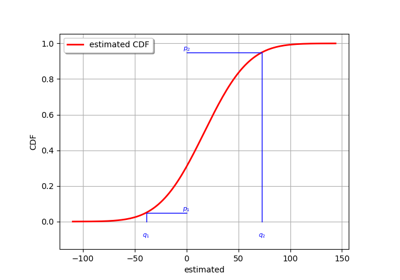
Estimation by matching quantiles.

Implements generic estimation by matching quantiles.

Parameters:

distributionDistribution: The distribution defining the parametric model to be adjusted to data. Its parameters define the starting point of the algorithm.
probabilitiessequence of float, optional: The probabilities $p_i \in [0,1]$ corresponding to the quantiles. The default value of the list of probabilities defined as follows. We define the interval $[\epsilon, 1 - \epsilon]$ where the value of $\epsilon$ is defined by the QuantileMatchingFactory-QuantileEpsilon key of the ResourceMap. A regular grid $\{p_i\}_{i = 1, ..., K}$ of probabilities is defined in the interval $[\epsilon, 1 - \epsilon]$ , where $K$ is the number of parameters of the distribution. The grid is defined by the equation $p_i = (1 - \rho_i) \epsilon + \rho_i (1 - \epsilon)$ where $\rho_i = \frac{i - 1}{K - 1}$ for $i = 1, ..., K$ .
boundsInterval, optional: Parameter bounds. The default bounds is an empty interval, which implies that the optimization problem is unbounded.

See also

DistributionFactory

Notes

We consider a distribution with $K$ parameters. Given a set of probabilities $p_1, ..., p_K \in [0, 1]$ and a set of quantiles $q_1, ..., q_K \in \Rset$ , we want to estimates the parameters of the distribution such that:

$\Prob{X \leq q_i} = p_i$

for $i = 1, ..., K$ . If a sample is given, then the quantiles are estimated from the data, which leads to the sample quantiles $\hat{q}_1, ..., \hat{q}_K$ .

The underlying optimization problem seeks to minimize the sum of slacks between the empirical quantiles of the sample and the quantiles of the parametric model:

$\Delta = \argmin_{\vect{\theta} \in \Rset^K} \sum_{i=1}^K (\hat{q}_i - q_i)^2$

where $K$ is the number of parameters of the distribution, $p_i$ the probabilities, and $\hat{q}_i$ is the sample quantile and $q_i$ is the quantile of the parametric distribution at the probabilities $p_1, ..., p_K$ .

Instead of using a sample, the buildFromQuantiles() method can be used if the quantiles are known. This can be useful if some expert knowledge is available.

Examples

Fit a distribution with 2 parameters. Hence, two quantiles are used to estimate the parameters.

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> sample = ot.Normal(0.9, 1.7).getSample(10)
>>> factory = ot.QuantileMatchingFactory(ot.Normal())
>>> inf_distribution = factory.build(sample)
>>> print(inf_distribution)
Normal(mu = 0.267484, sigma = 1.32218)
>>> print(factory.getProbabilities())
[0.01,0.99]

We see that the default value of the $\epsilon$ parameter is so that we consider the 1% and 99% percentile ranks.

Use 5% and 95% percentile ranks:

>>> probabilities = [0.05, 0.95]
>>> factory = ot.QuantileMatchingFactory(ot.Normal(), probabilities)
>>> inf_distribution = factory.build(sample)

With parameter bounds:

>>> bounds = ot.Interval([0.8, 1.6], [1.0, 1.8])
>>> factory = ot.QuantileMatchingFactory(ot.Normal())
>>> factory.setOptimizationBounds(bounds)
>>> inf_distribution = factory.build(sample)

An example with 4 parameters allows to see the default grid of probabilities in action.

>>> # A distribution with 4 parameters
>>> distribution = ot.Beta(2.0, 3.0, 4.0, 5.0)
>>> sample = distribution.getSample(10)
>>> distribution = ot.Beta()
>>> factory = ot.QuantileMatchingFactory(distribution)
>>> inf_distribution = factory.build(sample)
>>> print(factory.getProbabilities())
[0.01,0.336667,0.663333,0.99]

Methods

`build`(*args)	Build the distribution.
`buildEstimator`(*args)	Build the distribution and the parameter distribution.
`buildFromQuantiles`(quantiles)	Build from quantiles.
`getBootstrapSize`()	Accessor to the bootstrap size.
`getClassName`()	Accessor to the object's name.
`getId`()	Accessor to the object's id.
`getKnownParameterIndices`()	Accessor to the known parameters indices.
`getKnownParameterValues`()	Accessor to the known parameters indices.
`getName`()	Accessor to the object's name.
`getOptimizationAlgorithm`()	Accessor to the solver.
`getOptimizationBounds`()	Accessor to the optimization bounds.
`getProbabilities`()	Accessor to the probabilities.
`getShadowedId`()	Accessor to the object's shadowed id.
`getVisibility`()	Accessor to the object's visibility state.
`hasName`()	Test if the object is named.
`hasVisibleName`()	Test if the object has a distinguishable name.
`setBootstrapSize`(bootstrapSize)	Accessor to the bootstrap size.
`setKnownParameter`(values, positions)	Accessor to the known parameters.
`setName`(name)	Accessor to the object's name.
`setOptimizationAlgorithm`(solver)	Accessor to the solver.
`setOptimizationBounds`(optimizationBounds)	Accessor to the optimization bounds.
`setProbabilities`(probabilities)	Accessor to the fractiles.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setVisibility`(visible)	Accessor to the object's visibility state.

__init__(*args)¶

build(*args)¶

Build the distribution.

Available usages:

build(sample)

build(param)

Parameters:

sample2-d sequence of float: Sample from which the distribution parameters are estimated.
paramCollection of PointWithDescription: A vector of parameters of the distribution.

Returns:

distDistribution: The built distribution.

buildEstimator(*args)¶

Build the distribution and the parameter distribution.

Parameters:

sample2-d sequence of float: Sample from which the distribution parameters are estimated.
parametersDistributionParameters: Optional, the parametrization.

Returns:

resDistDistributionFactoryResult: The results.

Notes

According to the way the native parameters of the distribution are estimated, the parameters distribution differs:

Moments method: the asymptotic parameters distribution is normal and estimated by Bootstrap on the initial data;

Maximum likelihood method with a regular model: the asymptotic parameters distribution is normal and its covariance matrix is the inverse Fisher information matrix;

Other methods: the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting (see KernelSmoothing).

If another set of parameters is specified, the native parameters distribution is first estimated and the new distribution is determined from it:

if the native parameters distribution is normal and the transformation regular at the estimated parameters values: the asymptotic parameters distribution is normal and its covariance matrix determined from the inverse Fisher information matrix of the native parameters and the transformation;

in the other cases, the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting.

buildFromQuantiles(quantiles)¶

Build from quantiles.

Parameters:

quantilessequence of float: Quantiles of the distribution, matching the probabilities provided to the constructor.

Returns:

distDistribution: Estimated distribution.

Examples

>>> import openturns as ot
>>> distribution = ot.Beta(2.3, 2.2, -1.0, 1.0)
>>> probabilities = [0.05, 0.25, 0.75, 0.95]
>>> quantiles = [distribution.computeQuantile(pi)[0] for pi in probabilities] # Or from expert knowledge
>>> factory = ot.QuantileMatchingFactory(ot.Beta(), probabilities)
>>> inf_distribution = factory.buildFromQuantiles(quantiles)

getBootstrapSize()¶

Accessor to the bootstrap size.

Returns:

sizeinteger: Size of the bootstrap.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getKnownParameterIndices()¶

Accessor to the known parameters indices.

Returns:

indicesIndices: Indices of fixed parameters.

getKnownParameterValues()¶

Accessor to the known parameters indices.

Returns:

valuesPoint: Values of fixed parameters.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOptimizationAlgorithm()¶

Accessor to the solver.

Returns:

solverOptimizationAlgorithm: The solver used for numerical optimization of the moments.

getOptimizationBounds()¶

Accessor to the optimization bounds.

Returns:

boundsInterval: The bounds used for numerical optimization of the likelihood.

getProbabilities()¶

Accessor to the probabilities.

Returns:

probabilitiesPoint: The probabilities $p_i$

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

setBootstrapSize(bootstrapSize)¶

Accessor to the bootstrap size.

Parameters:

sizeinteger: Size of the bootstrap.

setKnownParameter(values, positions)¶

Accessor to the known parameters.

Parameters:

valuessequence of float: Values of fixed parameters.
indicessequence of int: Indices of fixed parameters.

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> distribution = ot.Beta(2.3, 2.2, -1.0, 1.0)
>>> sample = distribution.getSample(10)
>>> factory = ot.QuantileMatchingFactory(ot.Beta())
>>> # set (a,b) out of (r, t, a, b)
>>> factory.setKnownParameter([-1.0, 1.0], [2, 3])
>>> inf_distribution = factory.build(sample)

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setOptimizationAlgorithm(solver)¶

Accessor to the solver.

Parameters:

solverOptimizationAlgorithm: The solver used for numerical optimization of the moments.

setOptimizationBounds(optimizationBounds)¶

Accessor to the optimization bounds.

Parameters:

boundsInterval: The bounds used for numerical optimization of the likelihood.

setProbabilities(probabilities)¶

Accessor to the fractiles.

Parameters:

probabilitiessequence of float: The probabilities $p_i$

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters:

idint: Internal unique identifier.

setVisibility(visible)¶

Accessor to the object’s visibility state.

Parameters:

visiblebool: Visibility flag.

Examples using the class¶

Define a distribution from quantiles

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

QuantileMatchingFactory¶

Examples using the class¶