Note
Go to the end to download the full example code
Model a singular multivariate distribution¶
From time to time we need to model singular distributions
(e.g. the joint distribution of KL coefficients for curves resulting from the transport of a low dimensional random vector).
A way to do that is to use an
EmpiricalBernsteinCopula with a bin number equal to the sample size
(also called the empirical beta copula in this case).
import openturns as ot
import openturns.viewer as viewer
import math as m
ot.Log.Show(ot.Log.NONE)
ot.RandomGenerator.SetSeed(0)
routine to draw a distribution cloud and a sample
def draw(dist, Y):
g = ot.Graph()
g.setAxes(True)
g.setGrid(True)
c = ot.Cloud(dist.getSample(10000))
c.setColor("red")
c.setPointStyle("bullet")
g.add(c)
c = ot.Cloud(Y)
c.setColor("black")
c.setPointStyle("bullet")
g.add(c)
g.setBoundingBox(
ot.Interval(
Y.getMin() - 0.5 * Y.computeRange(), Y.getMax() + 0.5 * Y.computeRange()
)
)
return g
generate some multivariate data to estimate, with correlation
f = ot.SymbolicFunction(
["U", "xi1", "xi2"],
["sin(U)/(1+cos(U)^2)+0.05*xi1", "sin(U)*cos(U)/(1+cos(U)^2)+0.05*xi2"],
)
U = ot.Uniform(-0.85 * m.pi, 0.85 * m.pi)
xi = ot.Normal(2)
X = ot.BlockIndependentDistribution([U, xi])
N = 200
Y = f(X.getSample(N))
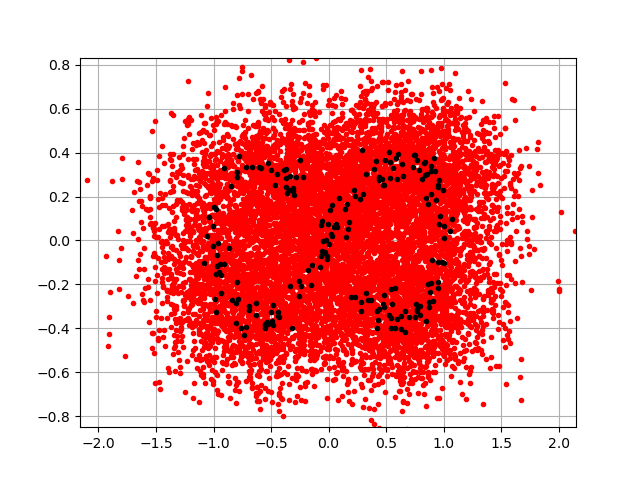
estimation by multivariate kernel smoothing
multi_ks = ot.KernelSmoothing().build(Y)
view = viewer.View(draw(multi_ks, Y))
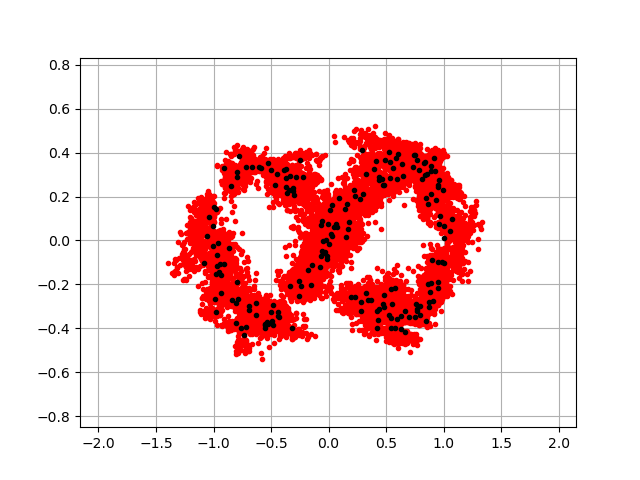
estimation by empirical beta copula
beta_copula = ot.EmpiricalBernsteinCopula(Y, len(Y))
marginals = [
ot.KernelSmoothing().build(Y.getMarginal(j)) for j in range(Y.getDimension())
]
beta_dist = ot.ComposedDistribution(marginals, beta_copula)
view = viewer.View(draw(beta_dist, Y))
viewer.View.ShowAll()
 OpenTURNS
OpenTURNS