Note

Go to the end to download the full example code

Estimate tail dependence coefficients on the wave-surge dataΒΆ

In this example we estimate the tail dependence coefficient of a bivariate sample applied to the concurrent measurements of two oceanographic variables (wave and surge heights) at a single location off south-west England. Readers should refer to [coles2001] to get more details.

First, we load the wave-surge dataset.

import openturns as ot
import openturns.viewer as otv
from openturns.usecases import coles

data = coles.Coles().wavesurge
print(data[:5])

graph = ot.Graph(
    "Concurent wave and surge heights", "wave (m)", "surge (m)", True, ""
)
cloud = ot.Cloud(data)
cloud.setColor("red")
graph.add(cloud)
view = otv.View(graph)
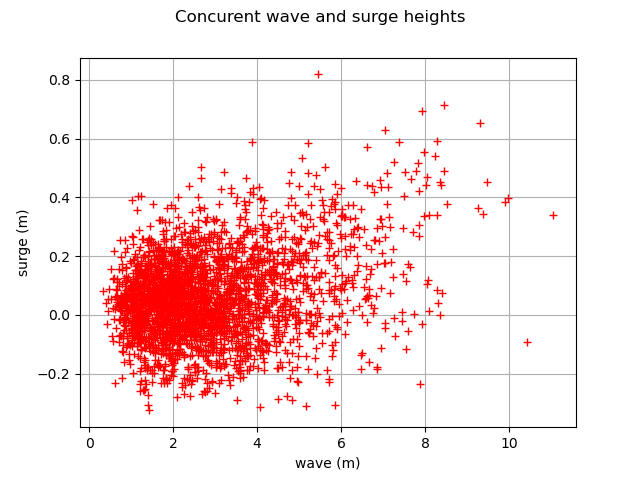
Concurent wave and surge heights
    [ wave   surge  ]
0 : [  1.5   -0.009 ]
1 : [  1.83  -0.053 ]
2 : [  2.44  -0.024 ]
3 : [  1.68   0     ]
4 : [  1.49   0.079 ]

We plot the graph of the function u \mapsto \chi(u) and the graph of the function u \mapsto \bar{\chi}(u). We conclude that both variables are asymptotially dependent as \chi > 0 and that they are positively correlated as \hat{\chi} > 0. We can visually deduce the upper tail dependence coefficient \chi \simeq 0.26 and the upper extremal dependence coefficient \bar{\chi} \simeq 0.5.

graph1 = ot.VisualTest.DrawUpperTailDependenceFunction(data)
graph2 = ot.VisualTest.DrawUpperExtremalDependenceFunction(data)
grid = ot.GridLayout(1, 2)
grid.setGraph(0, 0, graph1)
grid.setGraph(0, 1, graph2)
view = otv.View(grid)
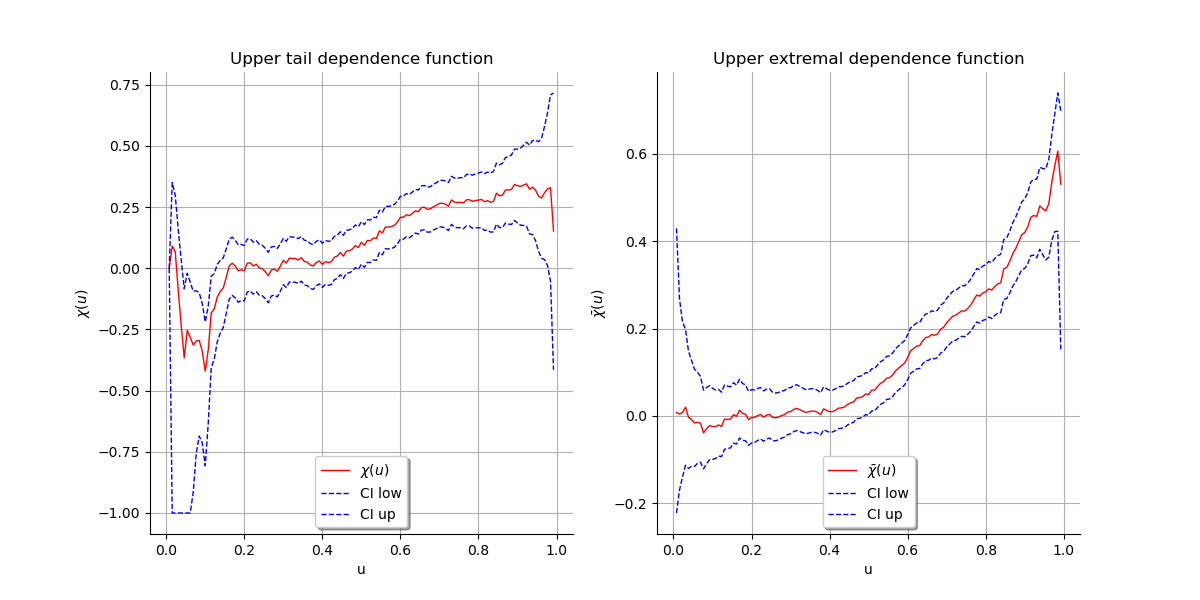
, Upper tail dependence function, Upper extremal dependence function
otv.View.ShowAll()