Note
Go to the end to download the full example code
Estimate correlation coefficients¶
In this example we are going to estimate the correlation between an output sample Y and the corresponding inputs using various estimators:
Pearson coefficients
Spearman coefficients
PCC: Partial Correlation Coefficients
PRCC: Partial Rank Correlation Coefficient
SRC: Standard Regression Coefficients
SRRC: Standard Rank Regression Coefficient
from openturns.usecases import ishigami_function
import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)
To illustrate the usage of the method mentioned above, we define a set of X/Y data using the Ishigami model. This classical model is defined in a data class :
im = ishigami_function.IshigamiModel()
Create X/Y data We get the input variables description :
input_names = im.distributionX.getDescription()
size = 100
inputDesign = ot.SobolIndicesExperiment(im.distributionX, size, True).generate()
outputDesign = im.model(inputDesign)
Create a CorrelationAnalysis object to compute various estimates
of the correlation between the inputs and the output.
corr_analysis = ot.CorrelationAnalysis(inputDesign, outputDesign)
PCC coefficients¶
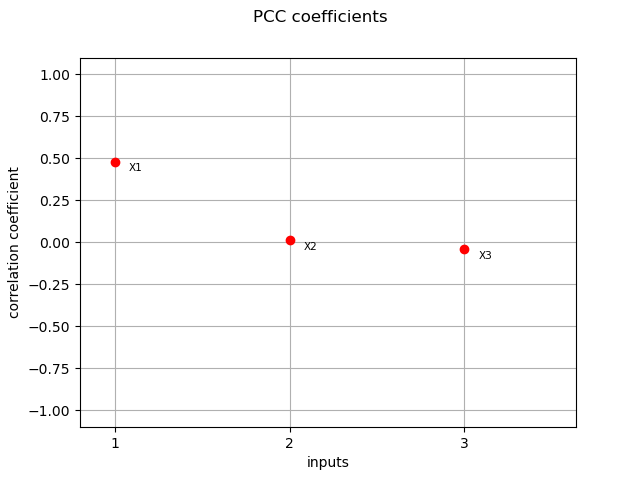
pcc_indices = corr_analysis.computePCC()
print(pcc_indices)
[0.48083,0.0118573,-0.0399335]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
pcc_indices, input_names, "PCC coefficients"
)
view = viewer.View(graph)
PRCC coefficients¶
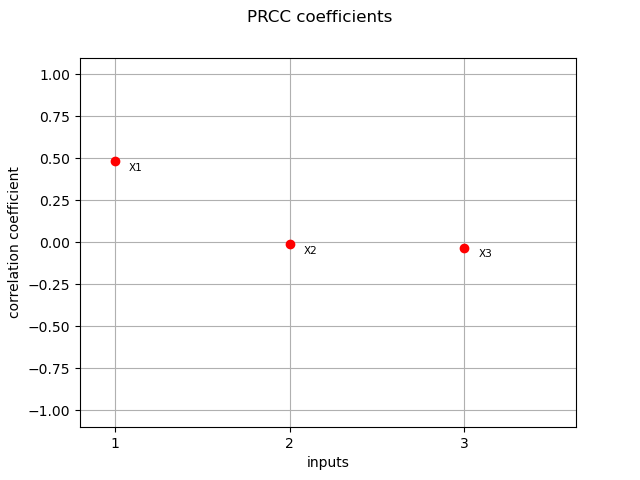
prcc_indices = corr_analysis.computePRCC()
print(prcc_indices)
[0.48438,-0.00850357,-0.0310585]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
prcc_indices, input_names, "PRCC coefficients"
)
view = viewer.View(graph)
SRC coefficients¶
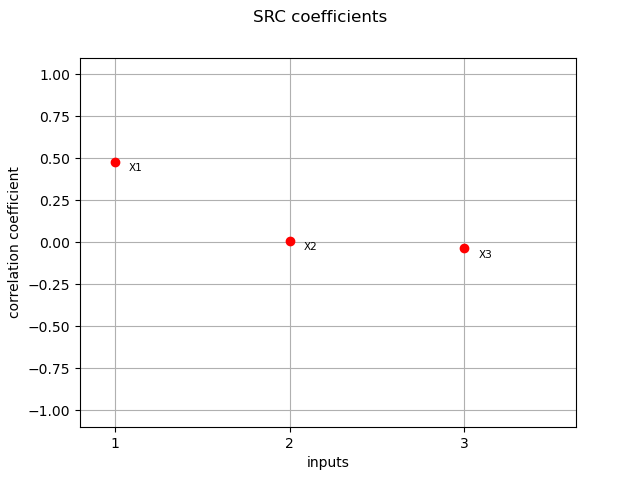
src_indices = corr_analysis.computeSRC()
print(src_indices)
[0.480662,0.0103814,-0.0350468]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
src_indices, input_names, "SRC coefficients"
)
view = viewer.View(graph)
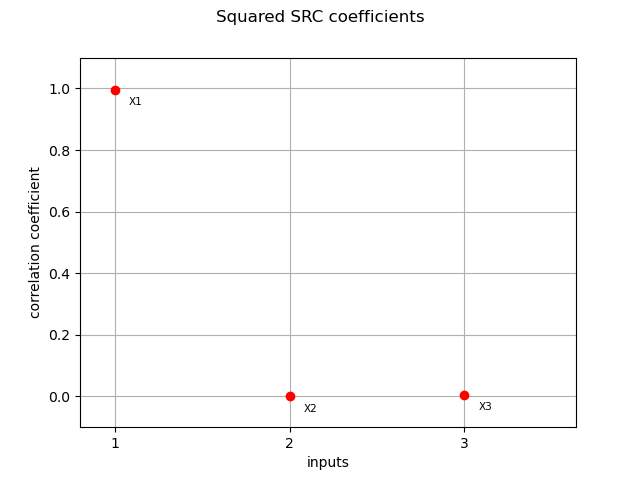
Normalized squared SRC coefficients (coefficients are made to sum to 1) :
squared_src_indices = corr_analysis.computeSquaredSRC(True)
print(squared_src_indices)
[0.99425,0.000463796,0.00528582]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
squared_src_indices, input_names, "Squared SRC coefficients"
)
view = viewer.View(graph)
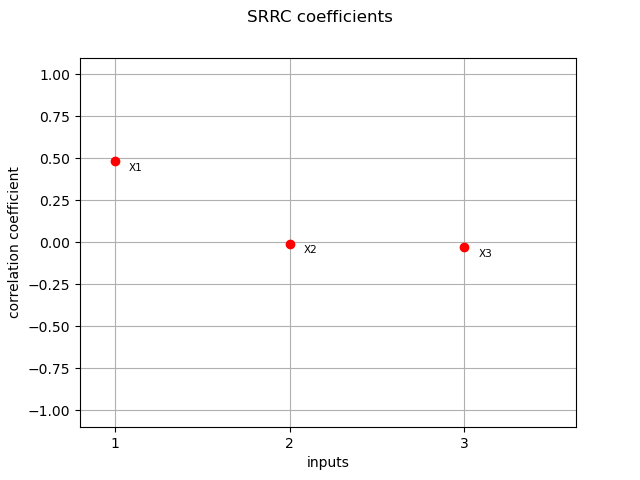
SRRC coefficients¶
srrc_indices = corr_analysis.computeSRRC()
print(srrc_indices)
[0.484588,-0.00743287,-0.0272169]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
srrc_indices, input_names, "SRRC coefficients"
)
view = viewer.View(graph)
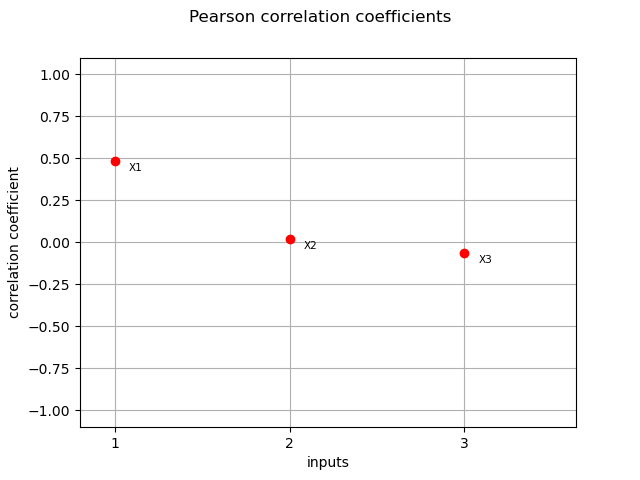
Pearson coefficients¶
We compute here the Pearson coefficients.
pearson_correlation = corr_analysis.computePearsonCorrelation()
print(pearson_correlation)
[0.482871,0.0178456,-0.0638373]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
pearson_correlation, input_names, "Pearson correlation coefficients"
)
view = viewer.View(graph)
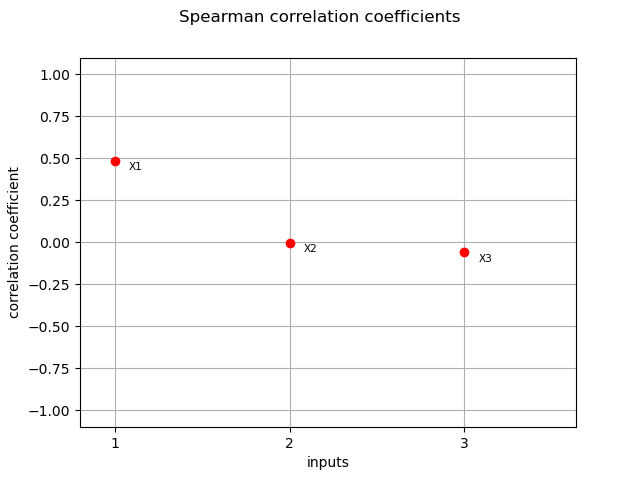
Spearman coefficients¶
We compute here the Spearman coefficients.
spearman_correlation = corr_analysis.computeSpearmanCorrelation()
print(spearman_correlation)
[0.486298,-0.00194796,-0.0585667]
graph = ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(
spearman_correlation, input_names, "Spearman correlation coefficients"
)
view = viewer.View(graph)
plt.show()
 OpenTURNS
OpenTURNS