Note

Go to the end to download the full example code

Create a linear least squares model

In this example we are going to create a global approximation of a model response based on a linear function using the LinearLeastSquares class.

We consider the function h : \Rset^2 \rightarrow \Rset^2 is defined by:

h(x_1, x_2) = \left(\cos(x_1 + x_2), (x_2 + 1) e^{x_1 - 2 x_2} \right)

for any \vect{x} \in \Rset^2. Since the output is a dimension 2 vector, the model has vector coefficients. We use the linear model:

\vect{y} \, \approx \, \widehat{\vect{h}}(\vect{x}) \, = \, \sum_{k=0}^2 \; \vect{a}_k \; \psi_k(\vect{x})

for any \vect{x} \in \Rset^2 where \left\{\vect{a}_k \in \Rset^2\right\}_{k = 0,..., 2} are the vector coefficients and \left\{\psi_k : \Rset^2 \rightarrow \Rset\right\}_{k = 0, ..., 2} are the basis functions. This implies that each marginal output \widehat{h}_i(\vect{x}) is approximated by the linear model:

\widehat{h}_i(\vect{x}) \, = \, \sum_{k=0}^2 \; a_{ki} \; \psi_k(\vect{x})

for any \vect{x} \in \Rset^2 and any i = 1, 2 where a_{ki} is the k-th coefficient of the i-th output marginal:

\vect{a}_k = \begin{pmatrix}a_{k1} \\ a_{k2} \end{pmatrix}

for k = 0, 1, 2. We consider the basis functions:

\psi_0(\vect{x}) & = 1 \\ \psi_1(\vect{x}) & = x_1 \\ \psi_2(\vect{x}) & = x_2 \\

for any \vect{x} \in \Rset^2.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

Define the model

Prepare an input sample. Each point is a pair of coordinates (x_1, x_2).

inputTrain = [[0.5, 0.5], [-0.5, -0.5], [-0.5, 0.5], [0.5, -0.5]]
inputTrain += [[0.25, 0.25], [-0.25, -0.25], [-0.25, 0.25], [0.25, -0.25]]
inputTrain = ot.Sample(inputTrain)
inputTrain.setDescription(["x1", "x2"])
inputTrain
x1x2
00.50.5
1-0.5-0.5
2-0.50.5
30.5-0.5
40.250.25
5-0.25-0.25
6-0.250.25
70.25-0.25


Compute the output sample from the input sample and a function.

formulas = ["cos(x1 + x2)", "(x2 + 1) * exp(x1 - 2 * x2)"]
model = ot.SymbolicFunction(["x1", "x2"], formulas)
model.setOutputDescription(["y1", "y2"])
outputTrain = model(inputTrain)
outputTrain
y1y2
00.54030230.909796
10.54030230.8243606
210.3346952
312.240845
40.87758260.973501
50.87758260.9630191
610.5904582
711.58775


Linear least squares

Create a linear least squares model.

algo = ot.LinearLeastSquares(inputTrain, outputTrain)
algo.run()

Get the linear term.

algo.getLinear()

[[ 9.93014e-17 0.998189 ]
[ 4.96507e-17 -0.925648 ]]



Get the constant term.

algo.getConstant()

[0.854471,1.05305]



Get the metamodel.

responseSurface = algo.getMetaModel()

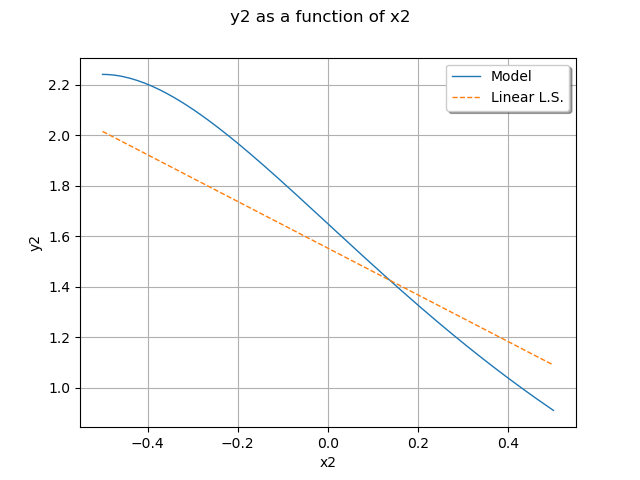
Plot the second output of our model with x_1=0.5.

graph = ot.ParametricFunction(model, [0], [0.5]).getMarginal(1).draw(-0.5, 0.5)
graph.setLegends(["Model"])
curve = (
    ot.ParametricFunction(responseSurface, [0], [0.5])
    .getMarginal(1)
    .draw(-0.5, 0.5)
    .getDrawable(0)
)
curve.setLineStyle("dashed")
curve.setLegend("Linear L.S.")
graph.add(curve)
graph.setLegendPosition("topright")
graph.setColors(ot.Drawable.BuildDefaultPalette(2))
view = viewer.View(graph)
plt.show()
y2 as a function of x2