Manipulate a time series¶

The objective here is to create and manipulate a time series. A time series is a particular field where the mesh $\mathcal{M}$ 1-d and regular, eg a time grid $(t_0, \dots, t_{N-1})$ .

It is possible to draw a time series, using interpolation between the values: see the use case on the Field.

A time series can be obtained as a realization of a multivariate stochastic process $X: \Omega \times [0,T] \rightarrow \mathbb{R}^d$ of dimension $d$ where $[0,T]$ is discretized according to the regular grid $(t_0, \dots, t_{N-1})$ . The values $(\underline{x}_0, \dots, \underline{x}_{N-1})$ of the time series are defined by:

$\forall i \in [0, N-1],\quad \underline{x}_i= X(\omega)(t_i)$

A time series is stored in the TimeSeries object that stores the regular time grid and the associated values.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

Create the RegularGrid

tMin = 0.0
timeStep = 0.1
N = 100
myTimeGrid = ot.RegularGrid(tMin, timeStep, N)

Case 1: Create a time series from a time grid and values Care! The number of steps of the time grid must correspond to the size of the values

myValues = ot.Normal(3).getSample(myTimeGrid.getVertices().getSize())
myTimeSeries = ot.TimeSeries(myTimeGrid, myValues)
myTimeSeries

[ t X0 X1 X2 ]
0 : [ 0 -1.40973 0.711103 -1.75418 ]
1 : [ 0.1 -1.33661 0.269893 1.41368 ]
2 : [ 0.2 0.499241 1.15854 -0.098967 ]
3 : [ 0.3 -0.650467 1.46114 0.61372 ]
4 : [ 0.4 2.14201 -1.66772 -0.151473 ]
5 : [ 0.5 2.4158 0.137289 -0.969704 ]
6 : [ 0.6 -0.292688 -1.02522 -0.354939 ]
7 : [ 0.7 -0.869302 0.266897 0.296524 ]
8 : [ 0.8 -2.24114 -1.5607 -2.272 ]
9 : [ 0.9 0.722451 -2.16128 -0.32861 ]
10 : [ 1 1.06975 -1.77994 -0.832708 ]
11 : [ 1.1 -0.245372 -0.0205006 -0.170101 ]
12 : [ 1.2 0.529296 -0.725104 -1.16247 ]
13 : [ 1.3 0.199523 0.727148 -0.260688 ]
14 : [ 1.4 -0.136772 0.52023 -0.659133 ]
15 : [ 1.5 -0.180673 -1.04885 0.512371 ]
16 : [ 1.6 0.20648 -0.960832 0.414682 ]
17 : [ 1.7 -1.22871 2.57497 -0.00804901 ]
18 : [ 1.8 -1.8859 0.830757 -0.378346 ]
19 : [ 1.9 0.479046 1.60938 -0.570841 ]
20 : [ 2 0.269096 0.803503 0.583218 ]
21 : [ 2.1 0.449756 -0.693556 1.89666 ]
22 : [ 2.2 0.0270818 -0.258272 -0.37012 ]
23 : [ 2.3 0.0456596 -0.343048 -0.392484 ]
24 : [ 2.4 -2.41093 1.93921 -0.590044 ]
25 : [ 2.5 0.22705 -0.141765 0.855507 ]
26 : [ 2.6 0.286761 0.564812 -0.509701 ]
27 : [ 2.7 1.40334 -1.37852 0.434035 ]
28 : [ 2.8 0.0342518 0.896116 -0.870577 ]
29 : [ 2.9 1.36995 0.272597 0.579223 ]
30 : [ 3 -1.5321 0.957065 0.427663 ]
31 : [ 3.1 -0.36668 0.648699 -0.00464944 ]
32 : [ 3.2 0.171548 -0.0795761 0.455389 ]
33 : [ 3.3 -2.14009 0.933245 0.818686 ]
34 : [ 3.4 -1.54826 0.370246 -0.773089 ]
35 : [ 3.5 -0.0129833 0.187309 -2.13145 ]
36 : [ 3.6 -1.19768 -0.00500185 -0.125673 ]
37 : [ 3.7 -1.89201 3.40565 -0.103576 ]
38 : [ 3.8 0.415448 0.727255 0.978855 ]
39 : [ 3.9 1.15808 0.295275 0.283934 ]
40 : [ 4 1.29426 0.200773 0.342265 ]
41 : [ 4.1 0.164085 -0.608383 0.144346 ]
42 : [ 4.2 0.537733 0.696557 1.18791 ]
43 : [ 4.3 2.18097 -0.194809 0.628316 ]
44 : [ 4.4 0.230866 -0.648071 -0.0280203 ]
45 : [ 4.5 0.871005 1.24473 -0.106358 ]
46 : [ 4.6 -0.234489 -2.0102 0.121701 ]
47 : [ 4.7 -1.33163 -0.825457 -1.21658 ]
48 : [ 4.8 -1.02579 -1.22486 -0.735057 ]
49 : [ 4.9 0.267431 -0.313967 0.328403 ]
50 : [ 5 -1.18542 0.272577 -0.537997 ]
51 : [ 5.1 -0.154628 0.0348939 0.357208 ]
52 : [ 5.2 0.87381 -1.4897 -1.60323 ]
53 : [ 5.3 0.276884 -0.205279 0.313591 ]
54 : [ 5.4 1.52063 2.12789 0.15741 ]
55 : [ 5.5 0.056432 1.05201 -1.06929 ]
56 : [ 5.6 0.0389696 0.108862 1.56022 ]
57 : [ 5.7 0.897858 0.0713179 0.329058 ]
58 : [ 5.8 0.768345 -0.201722 0.148307 ]
59 : [ 5.9 0.498826 -0.540609 0.202215 ]
60 : [ 6 1.52964 -1.19218 0.524954 ]
61 : [ 6.1 -0.127176 1.00122 0.299567 ]
62 : [ 6.2 -0.0732479 -0.592801 0.509773 ]
63 : [ 6.3 1.56808 0.369343 0.687346 ]
64 : [ 6.4 0.26022 1.5601 0.68388 ]
65 : [ 6.5 -0.260408 0.169652 -1.01657 ]
66 : [ 6.6 0.810285 -0.934548 0.440233 ]
67 : [ 6.7 0.102655 0.16255 0.977606 ]
68 : [ 6.8 -0.685128 -0.0411968 -0.161531 ]
69 : [ 6.9 0.00948899 -0.699237 0.835643 ]
70 : [ 7 0.961209 -0.395342 0.250509 ]
71 : [ 7.1 -1.71279 -0.303372 1.71343 ]
72 : [ 7.2 0.287997 -0.346204 -1.24308 ]
73 : [ 7.3 -0.661934 -0.539626 0.78918 ]
74 : [ 7.4 0.525199 0.265505 -0.615353 ]
75 : [ 7.5 0.667728 -0.320656 -0.00603524 ]
76 : [ 7.6 -1.44043 0.0706512 0.400517 ]
77 : [ 7.7 -0.537003 -2.13043 0.186229 ]
78 : [ 7.8 -1.32629 0.242601 -0.897333 ]
79 : [ 7.9 -0.957364 1.58824 -0.238077 ]
80 : [ 8 -0.654398 1.49892 -0.713136 ]
81 : [ 8.1 -1.33516 0.567629 0.640198 ]
82 : [ 8.2 -0.259729 0.192286 -1.40222 ]
83 : [ 8.3 0.560018 -1.35624 1.03452 ]
84 : [ 8.4 -0.378793 -0.125727 -0.587836 ]
85 : [ 8.5 1.07894 -1.66939 1.70834 ]
86 : [ 8.6 -0.845941 -0.178621 -0.195884 ]
87 : [ 8.7 1.81133 0.400036 1.10812 ]
88 : [ 8.8 -0.455236 -0.793417 2.28383 ]
89 : [ 8.9 0.351885 -0.0608221 1.18257 ]
90 : [ 9 2.05724 2.0836 -1.10946 ]
91 : [ 9.1 0.646117 0.314088 -1.25919 ]
92 : [ 9.2 2.51347 1.10677 -1.23708 ]
93 : [ 9.3 -0.405063 1.24478 0.258866 ]
94 : [ 9.4 -0.1138 0.3815 0.155791 ]
95 : [ 9.5 0.402412 1.33272 -0.805619 ]
96 : [ 9.6 0.385421 -1.61086 -0.687429 ]
97 : [ 9.7 -0.021074 -1.40527 -0.602909 ]
98 : [ 9.8 -0.0745371 -0.287633 -0.402623 ]
99 : [ 9.9 -0.489432 -0.580339 1.19649 ]

Case 2: Get a time series from a Process

myProcess = ot.WhiteNoise(ot.Normal(3), myTimeGrid)
myTimeSeries2 = myProcess.getRealization()
myTimeSeries2

	t	X0	X1	X2
0	0	1.004556	0.5372572	-0.08770909
1	0.1	1.423935	0.6820146	2.884055
2	0.2	0.2796988	-1.178997	-0.143892
3	0.3	0.6813079	0.01437919	0.5099701
4	0.4	-1.060234	0.04483657	0.2499197
5	0.5	1.24773	-0.3856004	-0.2880728
6	0.6	-0.5890517	0.4995753	1.132313
7	0.7	-0.8437811	1.43619	-0.1876503
8	0.8	0.940522	0.7151117	-1.439318
9	0.9	-0.1429401	-0.1765888	0.9054335
10	1	0.6688361	-0.1848348	-0.2056171
11	1.1	0.8539061	1.082717	0.7860448
12	1.2	-1.839514	-0.4807376	-0.7431111
13	1.3	0.2583894	0.06498678	0.8220976
14	1.4	-0.2202976	-1.267407	0.06548754
15	1.5	-2.506485	0.2182682	-0.3734256
16	1.6	-0.3483342	-1.020392	-0.9373684
17	1.7	0.793814	-0.983334	-0.4151898
18	1.8	0.1049272	-0.4991656	0.3643877
19	1.9	-0.1627931	0.4925782	0.3548167
20	2	-0.8811936	-0.819895	-2.106536
21	2.1	0.1773956	-0.04881701	-0.9867962
22	2.2	-0.8862132	1.219161	0.266691
23	2.3	0.188304	0.8090514	1.619885
24	2.4	-0.5646788	-0.9921044	0.7245245
25	2.5	0.3057475	-0.4119946	2.759856
26	2.6	0.4088039	1.121707	-0.6501654
27	2.7	-1.034288	1.150379	0.5587453
28	2.8	1.332409	-0.3225148	0.4750779
29	2.9	-0.1536095	1.035535	1.381175
30	3	1.225896	-0.1056646	0.3069166
31	3.1	0.4924758	0.4262604	-0.5698308
32	3.2	-0.4156163	-2.609303	-2.173168
33	3.3	-1.324497	-1.45585	0.1801837
34	3.4	1.421198	1.866039	-0.1742316
35	3.5	-1.55547	1.4884	1.303924
36	3.6	-1.061323	-1.305955	-1.629615
37	3.7	-0.2962869	0.8739792	0.1051378
38	3.8	-0.02998592	-1.516032	1.474471
39	3.9	-1.03669	-1.534651	0.8259901
40	4	0.457382	-0.3865615	1.28411
41	4.1	-0.3259461	1.637177	-0.8420178
42	4.2	-0.2924097	0.3615991	0.4570965
43	4.3	0.237978	1.020826	1.699262
44	4.4	-0.5438809	0.4973056	-1.469904
45	4.5	-2.294773	-0.2623551	-1.554523
46	4.6	-2.82731	0.5825531	0.4139608
47	4.7	-0.9302437	0.549059	-0.69065
48	4.8	-0.6021352	-0.7677184	1.285077
49	4.9	-0.22259	1.221741	0.4439343
50	5	-0.7078664	-1.056912	0.5648551
51	5.1	0.2980986	1.342418	1.085837
52	5.2	0.8239627	-0.6283856	-0.8834576
53	5.3	0.8607533	1.456264	0.1421699
54	5.4	-0.3323323	0.8952978	0.1655028
55	5.5	0.02714461	0.1645807	0.2626963
56	5.6	1.638611	0.1818056	-0.1240066
57	5.7	1.56386	-0.5471615	0.4136208
58	5.8	-0.5009097	-1.561814	-2.157897
59	5.9	-0.8845609	-0.03278067	-0.4371368
60	6	0.9263022	0.3640217	1.127778
61	6.1	-0.2958129	0.521623	-0.5048369
62	6.2	-1.126024	-0.1538759	0.9138794
63	6.3	-2.058274	1.093646	0.353957
64	6.4	-0.5708488	1.521397	0.2852253
65	6.5	-1.835236	-0.3044852	0.9165636
66	6.6	0.9140664	0.1075705	0.06927429
67	6.7	-0.6650488	1.951216	0.7997068
68	6.8	-0.8125796	-0.5797791	0.1117721
69	6.9	-0.2133026	-1.116885	-0.872058
70	7	1.629164	3.399959	-0.9405087
71	7.1	0.8080016	-0.5450092	1.626903
72	7.2	-0.06128802	0.308256	-0.9618253
73	7.3	-1.255094	0.4358796	-0.7273887
74	7.4	-0.3513546	-1.318261	-0.47417
75	7.5	-0.1005602	1.643525	-0.4139103
76	7.6	0.8686027	-0.4322521	1.012874
77	7.7	-1.114927	0.469528	0.9161205
78	7.8	-0.356955	1.022334	-2.00257
79	7.9	-1.71516	0.6274581	-1.352094
80	8	-0.03491598	-0.03793251	0.05596954
81	8.1	-0.2810947	0.144073	-2.171863
82	8.2	-0.3389453	0.5843859	-0.8390798
83	8.3	-1.04138	0.3519497	1.069267
84	8.4	-2.866462	1.182504	0.2067203
85	8.5	-0.6907754	-0.7425984	1.164752
86	8.6	-0.09003073	-1.209451	0.7730654
87	8.7	-0.8069562	-1.046643	0.1396704
88	8.8	1.067365	0.1232827	-0.776005
89	8.9	-0.882326	-0.0145659	0.2200673
90	9	0.4727389	-0.3159074	1.723677
91	9.1	0.5338985	0.4875888	-0.5419431
92	9.2	0.7959215	-0.9714537	-0.3666259
93	9.3	0.1363355	1.229809	-0.4606246
94	9.4	0.5330227	-0.9875807	0.2573491
95	9.5	0.415046	-0.7534109	0.07963906
96	9.6	0.5442014	-1.354907	-0.03364811
97	9.7	-0.7464795	-0.6355808	0.7484256
98	9.8	-1.11568	0.1287166	0.8080038
99	9.9	-0.5232872	-0.02984434	0.04724269

Get the number of values of the time series

myTimeSeries.getSize()

Get the dimension of the values observed at each time

myTimeSeries.getMesh().getDimension()

Get the value Xi at index i

i = 37
print("Xi = ", myTimeSeries.getValueAtIndex(i))

Xi =  [-1.89201,3.40565,-0.103576]

Get the time series at index i : Xi

i = 37
print("Xi = ", myTimeSeries[i])

Xi =  [-1.89201,3.40565,-0.103576]

Get a the marginal value at index i of the time series

i = 37
# get the time stamp:
print("ti = ", myTimeSeries.getTimeGrid().getValue(i))
# get the first component of the corresponding value :
print("Xi1 = ", myTimeSeries[i, 0])

ti =  3.7
Xi1 =  -1.892006989486264

Get all the values (X1, .., Xn) of the time series

myTimeSeries.getValues()

	X0	X1	X2
0	-1.409734	0.7111029	-1.754176
1	-1.336608	0.2698927	1.413675
2	0.4992414	1.158536	-0.09896703
3	-0.6504669	1.461145	0.6137203
4	2.142012	-1.667722	-0.1514732
5	2.4158	0.1372886	-0.9697043
6	-0.292688	-1.025222	-0.3549386
7	-0.8693017	0.266897	0.296524
8	-2.241144	-1.560704	-2.271998
9	0.7224505	-2.161275	-0.3286104
10	1.069747	-1.779941	-0.8327076
11	-0.2453716	-0.0205006	-0.1701006
12	0.5292955	-0.7251038	-1.162473
13	0.1995235	0.7271477	-0.2606875
14	-0.1367718	0.5202298	-0.6591333
15	-0.1806734	-1.048847	0.5123711
16	0.2064803	-0.960832	0.4146824
17	-1.228714	2.57497	-0.008049008
18	-1.885899	0.830757	-0.3783459
19	0.4790463	1.609382	-0.5708413
20	0.2690964	0.8035033	0.5832181
21	0.4497564	-0.6935559	1.896662
22	0.02708176	-0.258272	-0.37012
23	0.04565963	-0.3430478	-0.3924844
24	-2.410929	1.939206	-0.5900438
25	0.2270499	-0.1417654	0.8555065
26	0.286761	0.5648119	-0.5097008
27	1.403344	-1.378522	0.4340351
28	0.03425181	0.8961165	-0.8705775
29	1.369953	0.2725969	0.5792226
30	-1.532103	0.957065	0.4276634
31	-0.3666802	0.6486989	-0.004649441
32	0.1715484	-0.07957611	0.4553892
33	-2.140093	0.9332446	0.8186856
34	-1.548256	0.370246	-0.773089
35	-0.01298333	0.1873089	-2.131449
36	-1.197682	-0.005001849	-0.1256726
37	-1.892007	3.40565	-0.1035762
38	0.4154477	0.7272545	0.9788553
39	1.158081	0.2952752	0.2839339
40	1.294258	0.2007735	0.342265
41	0.1640854	-0.6083832	0.1443463
42	0.5377329	0.6965567	1.187906
43	2.180975	-0.1948093	0.6283156
44	0.2308662	-0.6480712	-0.02802031
45	0.8710046	1.244731	-0.1063582
46	-0.2344887	-2.010204	0.1217012
47	-1.331632	-0.8254575	-1.216578
48	-1.025789	-1.224865	-0.7350567
49	0.2674311	-0.3139666	0.3284034
50	-1.185418	0.2725766	-0.5379969
51	-0.1546276	0.03489387	0.3572081
52	0.8738098	-1.489697	-1.603233
53	0.2768838	-0.2052791	0.3135911
54	1.520626	2.127892	0.1574096
55	0.05643199	1.05201	-1.069286
56	0.03896958	0.1088619	1.560223
57	0.8978581	0.07131786	0.3290581
58	0.7683447	-0.2017215	0.1483074
59	0.4988259	-0.5406089	0.202215
60	1.52964	-1.192179	0.5249542
61	-0.1271758	1.001217	0.2995675
62	-0.07324792	-0.5928008	0.509773
63	1.568079	0.3693428	0.6873462
64	0.2602205	1.560101	0.6838802
65	-0.2604079	0.1696515	-1.016573
66	0.8102853	-0.9345477	0.4402335
67	0.1026545	0.1625502	0.9776058
68	-0.6851276	-0.04119683	-0.1615313
69	0.009488993	-0.6992373	0.8356431
70	0.9612086	-0.3953424	0.2505092
71	-1.712787	-0.3033722	1.713433
72	0.2879968	-0.3462038	-1.243077
73	-0.6619336	-0.5396257	0.7891796
74	0.525199	0.2655049	-0.6153533
75	0.6677281	-0.3206562	-0.00603524
76	-1.440427	0.07065125	0.4005165
77	-0.5370034	-2.130432	0.1862285
78	-1.326288	0.2426011	-0.8973327
79	-0.9573643	1.588237	-0.2380769
80	-0.6543979	1.498919	-0.7131357
81	-1.335157	0.5676285	0.640198
82	-0.259729	0.1922855	-1.402221
83	0.5600177	-1.356244	1.034522
84	-0.3787931	-0.1257271	-0.5878356
85	1.078941	-1.669386	1.708344
86	-0.8459409	-0.1786205	-0.1958844
87	1.811325	0.4000363	1.108118
88	-0.4552358	-0.7934174	2.283829
89	0.351885	-0.06082214	1.182574
90	2.057236	2.083603	-1.109457
91	0.6461174	0.3140881	-1.259195
92	2.51347	1.106768	-1.237082
93	-0.4050629	1.244775	0.2588656
94	-0.1137998	0.3814998	0.1557911
95	0.4024124	1.332716	-0.8056192
96	0.3854209	-1.61086	-0.6874292
97	-0.02107395	-1.405266	-0.6029087
98	-0.07453712	-0.287633	-0.4026233
99	-0.4894317	-0.5803388	1.196489

Compute the temporal Mean It corresponds to the mean of the values of the time series

myTimeSeries.getInputMean()

[0.0252771,0.032915,0.00141464]

Draw the marginal i of the time series using linear interpolation

graph = myTimeSeries.drawMarginal(0)
view = viewer.View(graph)

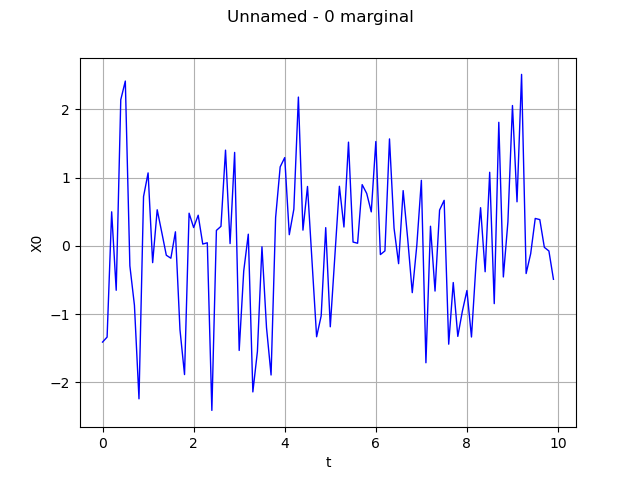
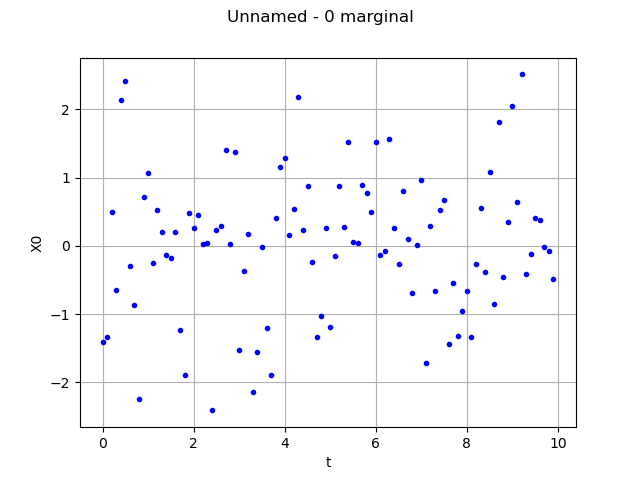
with no interpolation

graph = myTimeSeries.drawMarginal(0, False)
view = viewer.View(graph)
plt.show()

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

Manipulate a time series¶