Maximum Likelihood PrincipleΒΆ

This method deals with the parametric modeling of a probability distribution for a random vector \vect{X} = \left( X^1,\ldots,X^{n_X} \right). The appropriate probability distribution is found by using a sample of data \left\{ \vect{x}_1,\ldots,\vect{x}_N \right\}. Such an approach can be described in two steps as follows:

  • Choose a probability distribution (e.g. the Normal distribution, or any other distribution available),

  • Find the parameter values \vect{\theta} that characterize the probability distribution (e.g. the mean and standard deviation for the Normal distribution) which best describes the sample \left\{ \vect{x}_1,\ldots,\vect{x}_N \right\}.

The maximum likelihood method is used for the second step.

This method is restricted to the case where n_X = 1 and continuous probability distributions. Please note therefore that \vect{X} = X^1 = X in the following text. The maximum likelihood estimate (MLE) of \vect{\theta} is defined as the value of \vect{\theta} which maximizes the likelihood function L\left(X,\vect{\theta}\right):

\begin{aligned} \hat{\vect{\theta}} = \textrm{argmax}\ L\left(X,\vect{\theta} \right) \end{aligned}

Given that \left\{x_1,\ldots,x_N \right\} is a sample of independent identically distributed (i.i.d) observations, L\left(x_1,\ldots, x_N, \vect{\theta} \right) represents the probability of observing such a sample assuming that they are taken from a probability distribution with parameters \vect{\theta}. In concrete terms, the likelihood L\left(x_1,\ldots, x_N, \vect{\theta}\right) is calculated as follows:

L\left(x_1,\ldots, x_N, \vect{\theta} \right) = \prod_{j=1}^{N} f_X\left(x_j;\vect{\theta} \right)

if the distribution is continuous, with density f_X\left(x;\vect{\theta}\right).

For example, if we suppose that X is a Gaussian distribution with parameters \vect{\theta}= \{ \mu,\sigma \} (i.e. the mean and standard deviation),

\begin{aligned} L\left(x_1,\ldots, x_N, \vect{\theta}\right) &=& \prod_{j=1}^{N} \frac{1}{\sigma \sqrt{2\pi}} \exp \left[ -\frac{1}{2} \left( \frac{x_j-\mu}{\sigma} \right)^2 \right] \\ &=& \frac{1}{\sigma^N (2\pi)^{N/2}} \exp \left[ -\frac{1}{2\sigma^2} \sum_{j=1}^N \left( x_j-\mu \right)^2 \right] \end{aligned}

The following figure graphically illustrates the maximum likelihood method, in the particular case of a Gaussian probability distribution.

(Source code, png)

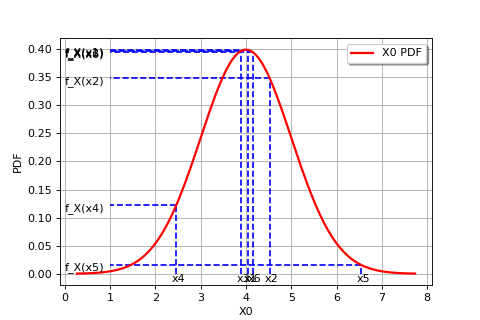
../../_images/maximum_likelihood-1.png

In general, in order to maximize the likelihood function classical optimization algorithms (e.g. gradient type) can be used. The Gaussian distribution case is an exception to this, as the maximum likelihood estimators are obtained analytically:

\begin{aligned} \widehat{\mu} = \frac{1}{N} \sum_{i=1}^N x_i,\ \widehat{\sigma^2} = \frac{1}{N} \sum_{i=1}^N \left( x_i - \widehat{\mu} \right)^2 \end{aligned}