SobolSimulationAlgorithm¶

(Source code, png)

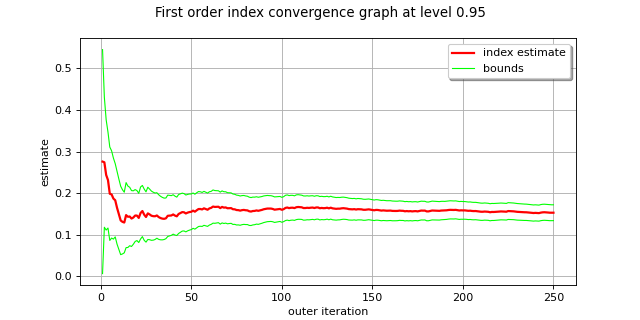
class SobolSimulationAlgorithm(*args)¶

Sobol indices computation using iterative sampling.

The algorithm uses sampling of the distribution of the random vector $\vect{X}$ through the model $f$ to iteratively estimate the Sobol indices.

At each iteration a fixed number $N = blockSize * (d + 2)$ of replications inputs is generated. These inputs are evaluated by blocks of size $batchSize$ through the model $f$ . Then the distribution of the indices (first and total order) is computed on this current replication sample. At the end of each iteration we update the global distribution of the indices.

Parameters:

XDistribution: The random vector to study.
fFunction: The function to study.
estimatorSobolIndicesAlgorithm: The estimator of the indices.

See also

SobolSimulationResult

Notes

The algorithm can operate on a multivariate model $f$ , in this case it operates on aggregated indices.

Several estimators are available (Saltelli, Jansen, …).

Let us denote by $n_X$ the number of input variables. For any $j = 1, \ldots, n_X$ , let us denote by $\Phi_j^F$ (resp. $\Phi_j^T$ ) the cumulated distribution function of the gaussian asymptotic distribution of the estimator of the Sobol’ first (resp. total) order indice. Let $\alpha\in[0,1]$ be the level of the confidence interval and $\epsilon\in(0,1]$ the length of this confidence interval. The algorithms stops when, on all components, first and total order indices haved been estimated with enough precision.

The precision is said to be sufficient if the length of the $\alpha$ -level confidence interval is smaller than $\epsilon$ :

$(\Phi_j^F)^{-1}(1-\alpha/2) - (\Phi_j^F)^{-1}(\alpha/2) \leq \epsilon \textrm{ and } (\Phi_j^T)^{-1}(1-\alpha/2) - (\Phi_j^T)^{-1}(\alpha/2) \leq \epsilon$

for all $j = 1, \ldots, n_X$ .

Examples

>>> import openturns as ot
>>> ot.RandomGenerator.SetSeed(0)
>>> distribution = ot.ComposedDistribution([ot.Uniform(-1.0, 1.0)] * 3)
>>> model = ot.SymbolicFunction(['x1', 'x2', 'x3'], ['x1*x2+x3'])
>>> estimator = ot.SaltelliSensitivityAlgorithm()
>>> estimator.setUseAsymptoticDistribution(True)
>>> algo = ot.SobolSimulationAlgorithm(distribution, model, estimator)
>>> algo.setMaximumOuterSampling(25) # number of iterations
>>> algo.setBlockSize(100) # size of Sobol experiment at each iteration
>>> algo.setBatchSize(4) # number of points evaluated simultaneously
>>> algo.setIndexQuantileLevel(0.05) # alpha
>>> algo.setIndexQuantileEpsilon(1e-2) # epsilon
>>> algo.run()
>>> result = algo.getResult()
>>> fo = result.getFirstOrderIndicesEstimate()
>>> foDist = result.getFirstOrderIndicesDistribution()

Methods

`drawFirstOrderIndexConvergence`(*args)	Draw the first order Sobol index convergence at a given level.
`drawTotalOrderIndexConvergence`(*args)	Draw the total order Sobol index convergence at a given level.
`getBatchSize`()	Accessor to the batch size.
`getBlockSize`()	Accessor to the block size.
`getClassName`()	Accessor to the object's name.
`getConvergenceStrategy`()	Accessor to the convergence strategy.
`getDistribution`()	Accessor to the batch size.
`getEstimator`()	Sobol estimator accessor.
`getId`()	Accessor to the object's id.
`getIndexQuantileEpsilon`()	Accessor to the criterion operator.
`getIndexQuantileLevel`()	Accessor to the quantile level.
`getMaximumCoefficientOfVariation`()	Accessor to the maximum coefficient of variation.
`getMaximumOuterSampling`()	Accessor to the maximum sample size.
`getMaximumStandardDeviation`()	Accessor to the maximum standard deviation.
`getName`()	Accessor to the object's name.
`getResult`()	Accessor to the result.
`getShadowedId`()	Accessor to the object's shadowed id.
`getVerbose`()	Accessor to verbosity.
`getVisibility`()	Accessor to the object's visibility state.
`hasName`()	Test if the object is named.
`hasVisibleName`()	Test if the object has a distinguishable name.
`run`()	Launch simulation.
`setBatchSize`(replicationSize)	Accessor to the batch size.
`setBlockSize`(blockSize)	Accessor to the block size.
`setConvergenceStrategy`(convergenceStrategy)	Accessor to the convergence strategy.
`setEstimator`(estimator)	Sobol estimator accessor.
`setIndexQuantileEpsilon`(indexQuantileEpsilon)	Accessor to the quantile tolerance.
`setIndexQuantileLevel`(indexQuantileLevel)	Accessor to the quantile level.
`setMaximumCoefficientOfVariation`(...)	Accessor to the maximum coefficient of variation.
`setMaximumOuterSampling`(maximumOuterSampling)	Accessor to the maximum sample size.
`setMaximumStandardDeviation`(...)	Accessor to the maximum standard deviation.
`setName`(name)	Accessor to the object's name.
`setProgressCallback`(*args)	Set up a progress callback.
`setShadowedId`(id)	Accessor to the object's shadowed id.
`setStopCallback`(*args)	Set up a stop callback.
`setVerbose`(verbose)	Accessor to verbosity.
`setVisibility`(visible)	Accessor to the object's visibility state.

__init__(*args)¶

drawFirstOrderIndexConvergence(*args)¶

Draw the first order Sobol index convergence at a given level.

Parameters:

marginalIndexint: Index of the random vector component to consider
levelfloat, optional: The expectation convergence is drawn at this given confidence length level. By default level is 0.95.

Returns:

grapha Graph: expectation convergence graph

drawTotalOrderIndexConvergence(*args)¶

Draw the total order Sobol index convergence at a given level.

Parameters:

marginalIndexint: Index of the random vector component to consider
levelfloat, optional: The expectation convergence is drawn at this given confidence length level. By default level is 0.95.

Returns:

grapha Graph: expectation convergence graph

getBatchSize()¶

Accessor to the batch size.

Returns:

batchSizeint: Number of points evaluated simultaneously.

getBlockSize()¶

Accessor to the block size.

Returns:

blockSizeint: Number of terms in the probability simulation estimator grouped together. It is set by default to 1.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getConvergenceStrategy()¶

Accessor to the convergence strategy.

Returns:

storage_strategyHistoryStrategy: Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.

getDistribution()¶

Accessor to the batch size.

Returns:

distributionDistribution: Distribution of the random variable.

getEstimator()¶

Sobol estimator accessor.

Returns:

estimatorSobolIndicesAlgorithm: The estimator of the indices.

getId()¶

Accessor to the object’s id.

Returns:

idint: Internal unique identifier.

getIndexQuantileEpsilon()¶

Accessor to the criterion operator.

Returns:

epsilonfloat: The quantile tolerance

getIndexQuantileLevel()¶

Accessor to the quantile level.

Returns:

alphafloat: The quantile level.

getMaximumCoefficientOfVariation()¶

Accessor to the maximum coefficient of variation.

Returns:

coefficientfloat: Maximum coefficient of variation of the simulated sample.

getMaximumOuterSampling()¶

Accessor to the maximum sample size.

Returns:

outerSamplingint: Maximum number of groups of terms in the probability simulation estimator.

getMaximumStandardDeviation()¶

Accessor to the maximum standard deviation.

Returns:

sigmafloat, $\sigma > 0$: Maximum standard deviation of the estimator.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getResult()¶

Accessor to the result.

Returns:

resultSobolSimulationResult: The simulation result.

getShadowedId()¶

Accessor to the object’s shadowed id.

Returns:

idint: Internal unique identifier.

getVerbose()¶

Accessor to verbosity.

Returns:

verbosity_enabledbool: If True, the computation is verbose. By default it is verbose.

getVisibility()¶

Accessor to the object’s visibility state.

Returns:

visiblebool: Visibility flag.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

hasVisibleName()¶

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool: True if the name is not empty and not the default one.

run()¶

Launch simulation.

See also

setBlockSize, setMaximumOuterSampling, ResourceMap, SimulationResult

Notes

It launches the simulation on a sample of size at most outerSampling * blockSize, this sample being built by blocks of size blockSize. It allows one to use efficiently the distribution of the computation as well as it allows one to deal with a sample size $> 2^{32}$ by a combination of blockSize and outerSampling.

setBatchSize(replicationSize)¶

Accessor to the batch size.

Parameters:

batchSizeint: Number of points evaluated simultaneously.

setBlockSize(blockSize)¶

Accessor to the block size.

Parameters:

blockSizeint, $blockSize \geq 1$: Number of terms in the probability simulation estimator grouped together. It is set by default to 1.

Notes

For Monte Carlo, LHS and Importance Sampling methods, this allows one to save space while allowing multithreading, when available we recommend to use the number of available CPUs; for the Directional Sampling, we recommend to set it to 1.

setConvergenceStrategy(convergenceStrategy)¶

Accessor to the convergence strategy.

Parameters:

storage_strategyHistoryStrategy: Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.

setEstimator(estimator)¶

Sobol estimator accessor.

Parameters:

estimatorSobolIndicesAlgorithm: The estimator of the indices.

setIndexQuantileEpsilon(indexQuantileEpsilon)¶

Accessor to the quantile tolerance.

Parameters:

epsilonfloat: The quantile tolerance

setIndexQuantileLevel(indexQuantileLevel)¶

Accessor to the quantile level.

Parameters:

alphafloat: The quantile level.

setMaximumCoefficientOfVariation(maximumCoefficientOfVariation)¶

Accessor to the maximum coefficient of variation.

Parameters:

coefficientfloat: Maximum coefficient of variation of the simulated sample.

setMaximumOuterSampling(maximumOuterSampling)¶

Accessor to the maximum sample size.

Parameters:

outerSamplingint: Maximum number of groups of terms in the probability simulation estimator.

setMaximumStandardDeviation(maximumStandardDeviation)¶

Accessor to the maximum standard deviation.

Parameters:

sigmafloat, $\sigma > 0$: Maximum standard deviation of the estimator.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setProgressCallback(*args)¶

Set up a progress callback.

Can be used to programmatically report the progress of a simulation.

Parameters:

callbackcallable: Takes a float as argument as percentage of progress.

Examples

>>> import sys
>>> import openturns as ot
>>> experiment = ot.MonteCarloExperiment()
>>> X = ot.RandomVector(ot.Normal())
>>> Y = ot.CompositeRandomVector(ot.SymbolicFunction(['X'], ['1.1*X']), X)
>>> event = ot.ThresholdEvent(Y, ot.Less(), -2.0)
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(100)
>>> algo.setMaximumCoefficientOfVariation(-1.0)
>>> def report_progress(progress):
...     sys.stderr.write('-- progress=' + str(progress) + '%\n')
>>> algo.setProgressCallback(report_progress)
>>> algo.run()

setShadowedId(id)¶

Accessor to the object’s shadowed id.

Parameters:

idint: Internal unique identifier.

setStopCallback(*args)¶

Set up a stop callback.

Can be used to programmatically stop a simulation.

Parameters:

callbackcallable: Returns an int deciding whether to stop or continue.

Examples

Stop a Monte Carlo simulation algorithm using a time limit

>>> import openturns as ot
>>> experiment = ot.MonteCarloExperiment()
>>> X = ot.RandomVector(ot.Normal())
>>> Y = ot.CompositeRandomVector(ot.SymbolicFunction(['X'], ['1.1*X']), X)
>>> event = ot.ThresholdEvent(Y, ot.Less(), -2.0)
>>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
>>> algo.setMaximumOuterSampling(10000000)
>>> algo.setMaximumCoefficientOfVariation(-1.0)
>>> timer = ot.TimerCallback(0.1)
>>> algo.setStopCallback(timer)
>>> algo.run()

setVerbose(verbose)¶

Accessor to verbosity.

Parameters:

verbosity_enabledbool: If True, make the computation verbose. By default it is verbose.

setVisibility(visible)¶

Accessor to the object’s visibility state.

Parameters:

visiblebool: Visibility flag.

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

SobolSimulationAlgorithm¶