Note

Go to the end to download the full example code

Estimate a conditional quantile

# sphinx_gallery_thumbnail_number = 8

From a multivariate data sample, we estimate a distribution with kernel smoothing. Here we present a bivariate distribution X= (X_1, X_2). We use the computeConditionalQuantile method to estimate the 90% quantile Q_1 of the conditional variable X_2|X_1 :

Q_2 : x_1 \mapsto q_{0.9}(X_2|X_1=x_1)

We then draw the curve Q_2 : x_1 \mapsto Q_2(x_1). We first start with independent normals then we consider dependent marginals with a Clayton copula.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
import numpy as np

ot.Log.Show(ot.Log.NONE)

Set the random generator seed

ot.RandomGenerator.SetSeed(0)

Defining the marginals

We consider two independent normal marginals :

X1 = ot.Normal(0.0, 1.0)
X2 = ot.Normal(0.0, 3.0)

Independent marginals

distX = ot.ComposedDistribution([X1, X2])
sample = distX.getSample(1000)

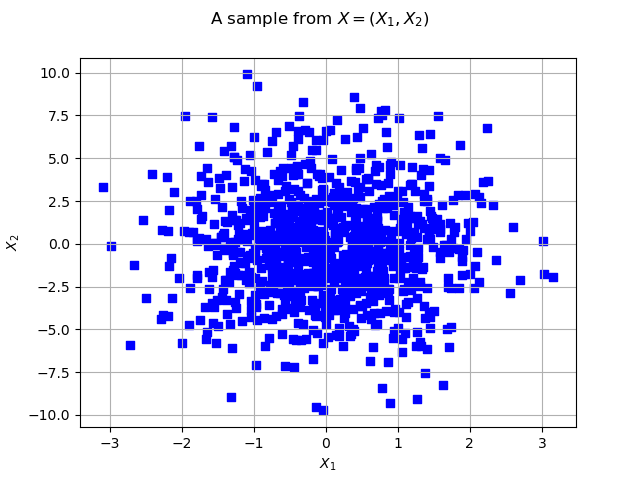
Let’s see the data

graph = ot.Graph("2D-Normal sample", "x1", "x2", True, "")
cloud = ot.Cloud(sample, "blue", "fsquare", "My Cloud")
graph.add(cloud)
graph.setXTitle("$X_1$")
graph.setYTitle("$X_2$")
graph.setTitle("A sample from $X=(X_1, X_2)$")
view = viewer.View(graph)
A sample from $X=(X_1, X_2)$

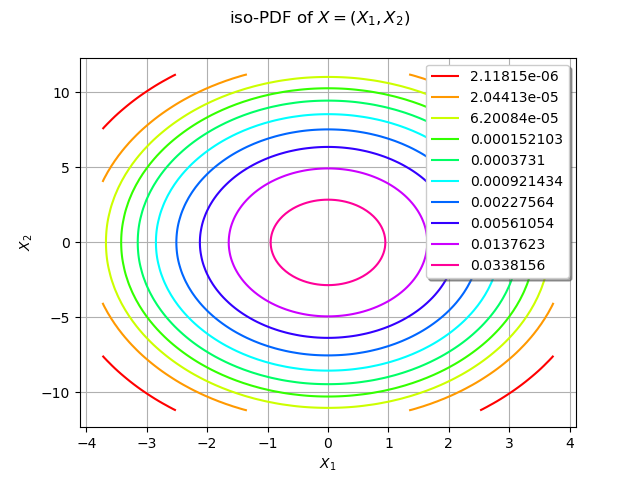
We draw the isolines of the PDF of X :

graph = distX.drawPDF()
graph.setXTitle("$X_1$")
graph.setYTitle("$X_2$")
graph.setTitle("iso-PDF of $X=(X_1, X_2)$")
view = viewer.View(graph)
iso-PDF of $X=(X_1, X_2)$

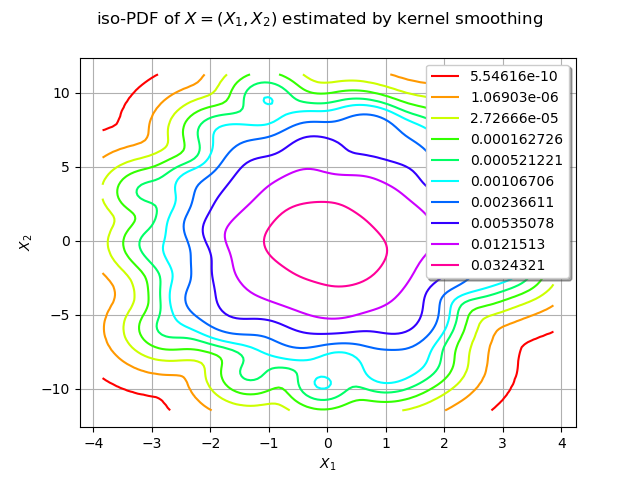
We estimate the density with kernel smoothing :

kernel = ot.KernelSmoothing()
estimated = kernel.build(sample)

We draw the isolines of the estimated PDF of X :

graph = estimated.drawPDF()
graph.setXTitle("$X_1$")
graph.setYTitle("$X_2$")
graph.setTitle("iso-PDF of $X=(X_1, X_2)$ estimated by kernel smoothing")
view = viewer.View(graph)
iso-PDF of $X=(X_1, X_2)$ estimated by kernel smoothing

We can compute the conditional quantile of X_2 | X_1 with the computeConditionalQuantile method and draw it after.

We first create N observation points in [-3.0, 3.0] :

N = 301
xobs = np.linspace(-3.0, 3.0, N)
sampleObs = ot.Sample([[xi] for xi in xobs])

We create curves of the exact and approximated quantile Q_1

x = [xi for xi in xobs]
yapp = [estimated.computeConditionalQuantile(0.9, sampleObs[i]) for i in range(N)]
yex = [distX.computeConditionalQuantile(0.9, sampleObs[i]) for i in range(N)]

cxy_app = ot.Curve(x, yapp)
cxy_ex = ot.Curve(x, yex)
graph = ot.Graph("90% quantile of $X_2 | X_1=x_1$", "$x_1$", "$Q_2(x_1)$", True, "")
graph.add(cxy_app)
graph.add(cxy_ex)
graph.setLegends(["$Q_2$ kernel smoothing", "$Q_2$ exact"])
graph.setLegendPosition("lower right")
graph.setColors(["red", "blue"])
view = viewer.View(graph)
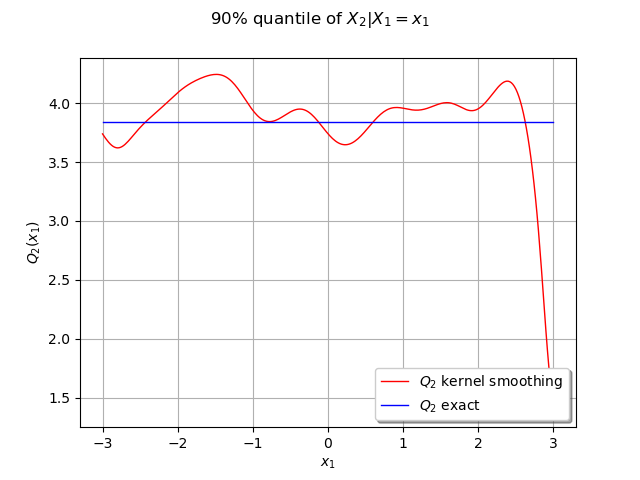
90% quantile of $X_2 | X_1=x_1$

In this case the Q_2 quantile is constant because of the independence of the marginals.

Dependence through a Clayton copula

We now define a Clayton copula to model the dependence between our marginals. The Clayton copula is a bivariate asymmmetric Archimedean copula, exhibiting greater dependence in the negative tail than in the positive.

copula = ot.ClaytonCopula(2.5)
distX = ot.ComposedDistribution([X1, X2], copula)

We generate a sample from the distribution :

sample = distX.getSample(1000)

Let’s see the data

graph = ot.Graph("2D-Normal sample", "x1", "x2", True, "")
cloud = ot.Cloud(sample, "blue", "fsquare", "My Cloud")
graph.add(cloud)
graph.setXTitle("$X_1$")
graph.setYTitle("$X_2$")
graph.setTitle("A sample from $X=(X_1, X_2)$")
view = viewer.View(graph)
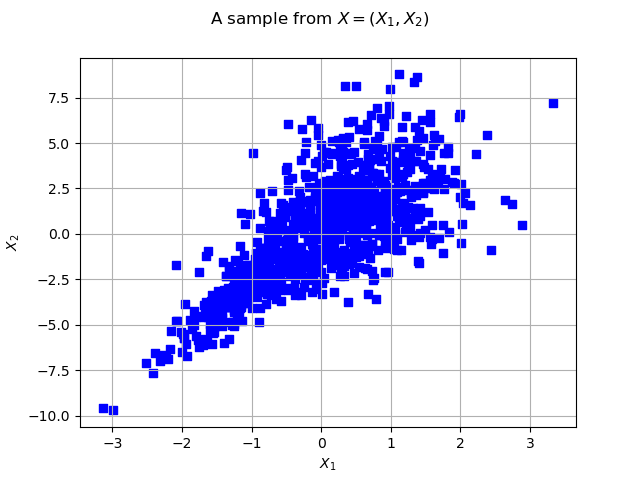
A sample from $X=(X_1, X_2)$

We draw the isolines of the PDF of X :

graph = distX.drawPDF()
graph.setXTitle("$X_1$")
graph.setYTitle("$X_2$")
graph.setTitle("iso-PDF of $X=(X_1, X_2)$")
view = viewer.View(graph)
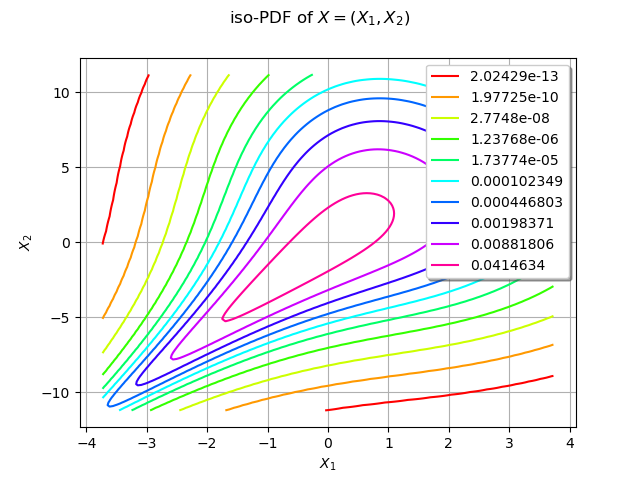
iso-PDF of $X=(X_1, X_2)$

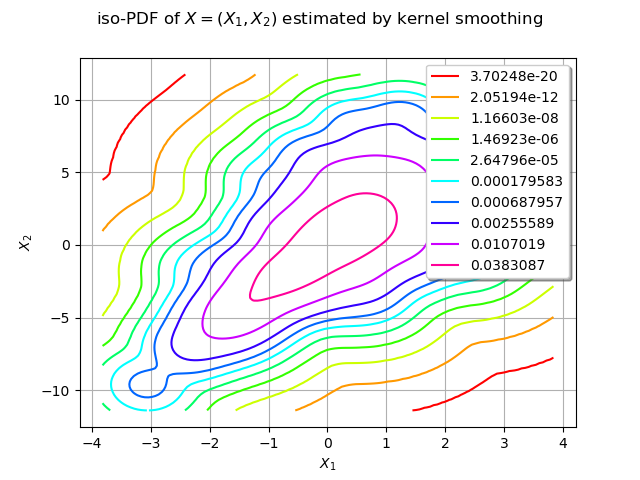
We estimate the density with kernel smoothing :

kernel = ot.KernelSmoothing()
estimated = kernel.build(sample)

We draw the isolines of the estimated PDF of X :

graph = estimated.drawPDF()
graph.setXTitle("$X_1$")
graph.setYTitle("$X_2$")
graph.setTitle("iso-PDF of $X=(X_1, X_2)$ estimated by kernel smoothing")
view = viewer.View(graph)
iso-PDF of $X=(X_1, X_2)$ estimated by kernel smoothing

We can compute the conditional quantile of X_2 | X_1=x1 with the computeConditionalQuantile method and draw it after.

We first create N observation points in [-3.0, 3.0] :

N = 301
xobs = np.linspace(-3.0, 3.0, N)
sampleObs = ot.Sample([[xi] for xi in xobs])

We create curves of the exact and approximated quantile Q_1

x = [xi for xi in xobs]
yapp = [estimated.computeConditionalQuantile(0.9, sampleObs[i]) for i in range(N)]
yex = [distX.computeConditionalQuantile(0.9, sampleObs[i]) for i in range(N)]

cxy_app = ot.Curve(x, yapp)
cxy_ex = ot.Curve(x, yex)
graph = ot.Graph("90% quantile of $X_2 | X_1=x_1$", "$x_1$", "$Q_2(x_1)$", True, "")
graph.add(cxy_app)
graph.add(cxy_ex)
graph.setLegends(["$Q_2$ kernel smoothing", "$Q_2$ exact"])
graph.setLegendPosition("lower right")
graph.setColors(["red", "blue"])
view = viewer.View(graph)
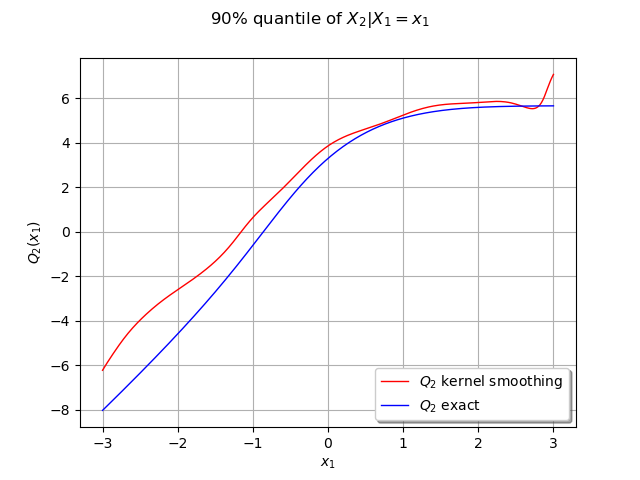
90% quantile of $X_2 | X_1=x_1$

Our estimated conditional quantile is a good approximate and should be better the more data we have. We can observe it by increasing the number of samples.

plt.show()