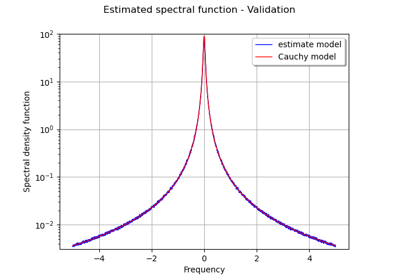
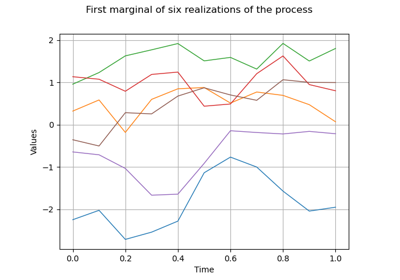
CauchyModel

(Source code, png)

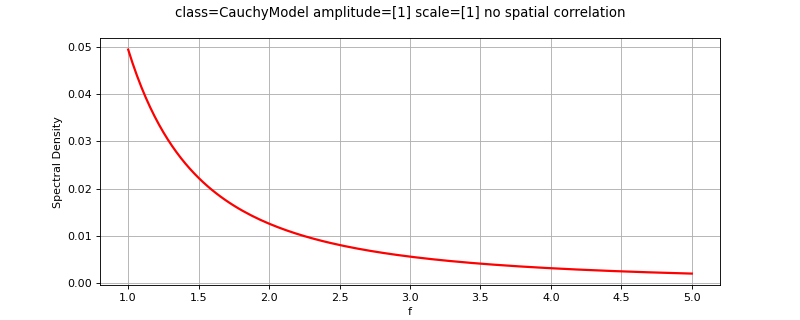
../../_images/openturns-CauchyModel-1.png
class CauchyModel(*args)

Cauchy spectral model.

Refer to Parametric spectral density functions.

Available constructors:

CauchyModel(theta, sigma)

Parameters:
thetasequence of float

Scale coefficients \theta of the spectral density function. Vector of size n

sigmasequence of float

Amplitude coefficients \sigma of the spectral density function. Vector of size p

Notes

The spectral density function of input dimension n and output dimension p writes:

\forall (i,j) \in [0,p-1]^2, S(f)_{i,j} = 2 \Sigma_{i,j} \prod_{k=1}^{n} \frac{\theta_k}{1 + (2\pi \theta_k f)^2}

Examples

>>> import openturns as ot
>>> spectralModel = ot.CauchyModel([3.0, 2.0], [2.0])
>>> f = 0.3
>>> print(spectralModel(f))
[[ (0.191364,0) ]]
>>> f = 10
>>> print(spectralModel(f))
[[ (1.71084e-07,0) ]]

Methods

__call__(frequency)

Evaluate the spectral density function for a specific frequency.

computeStandardRepresentative(frequency)

Compute the standard representant of the spectral density function.

draw(*args)

Draw a specific component of the spectral density function.

getAmplitude()

Get the amplitude parameter of the spectral density function.

getClassName()

Accessor to the object's name.

getId()

Accessor to the object's id.

getInputDimension()

Get the input dimension of the spectral density function.

getName()

Accessor to the object's name.

getOutputCorrelation()

Get the spatial correlation matrix of the spectral density function.

getOutputDimension()

Get the dimension of the SpectralModel.

getScale()

Get the scale parameter of the spectral density function.

getShadowedId()

Accessor to the object's shadowed id.

getVisibility()

Accessor to the object's visibility state.

hasName()

Test if the object is named.

hasVisibleName()

Test if the object has a distinguishable name.

setAmplitude(amplitude)

Set the amplitude parameter of the spectral density function.

setName(name)

Accessor to the object's name.

setScale(scale)

Set the scale parameter of the spectral density function.

setShadowedId(id)

Accessor to the object's shadowed id.

setVisibility(visible)

Accessor to the object's visibility state.
__init__(*args)
computeStandardRepresentative(frequency)

Compute the standard representant of the spectral density function.

Parameters:
taufloat

Frequency value.

Returns:
rhoComplex

Standard representant factor of the spectral density function.

Notes

Using definitions in SpectralModel: the standard representative function writes:

\forall \vect{f} \in \Rset^n, \rho(\vect{f} \odot \vect{\theta}) = \prod_{k=1}^{n} \frac{1}{1 + (2\pi \theta_k f)^2}

where (\vect{f} \odot \vect{\theta})_k = \vect{f}_k \vect{\theta}_k

draw(*args)

Draw a specific component of the spectral density function.

Parameters:
rowIndexint, 0 \leq rowIndex < dimension

The row index of the component to draw. Default value is 0.

columnIndex: int, :math:`0 leq columnIndex < dimension`

The column index of the component to draw. Default value is 0.

minimumFrequencyfloat

The lower bound of the frequency range over which the model is plotted. Default value is SpectralModel-DefaultMinimumFrequency in ResourceMap.

maximumFrequencyfloat

The upper bound of the frequency range over which the model is plotted. Default value is SpectralModel-DefaultMaximumFrequency in ResourceMap.

frequencyNumberint, pointNumber \geq 2

The discretization of the frequency range [minimumFrequency, maximumFrequency] over which the model is plotted. Default value is SpectralModel-DefaultFrequencyNumber in class:~openturns.ResourceMap.

modulebool

Flag to tell if module has to be drawn (True) or if it is the argument to be drawn (False). Default value is True.

Returns:
graphGraph

Graphic of the specified component

getAmplitude()

Get the amplitude parameter of the spectral density function.

Returns:
amplitudePoint

The used amplitude parameter.

getClassName()

Accessor to the object’s name.

Returns:
class_namestr

The object class name (object.__class__.__name__).

getId()

Accessor to the object’s id.

Returns:
idint

Internal unique identifier.

getInputDimension()

Get the input dimension of the spectral density function.

Returns:
inputDimensionint

SpatialDimension of the SpectralModel.

getName()

Accessor to the object’s name.

Returns:
namestr

The name of the object.

getOutputCorrelation()

Get the spatial correlation matrix of the spectral density function.

Returns:
spatialCorrelationCorrelationMatrix

Correlation matrix \mat{R} \in \mathcal{M}_{dimension \times dimension}([-1, 1]).

getOutputDimension()

Get the dimension of the SpectralModel.

Returns:
dimensionint

Dimension of the SpectralModel.

getScale()

Get the scale parameter of the spectral density function.

Returns:
scalePoint

The used scale parameter.

getShadowedId()

Accessor to the object’s shadowed id.

Returns:
idint

Internal unique identifier.

getVisibility()

Accessor to the object’s visibility state.

Returns:
visiblebool

Visibility flag.

hasName()

Test if the object is named.

Returns:
hasNamebool

True if the name is not empty.

hasVisibleName()

Test if the object has a distinguishable name.

Returns:
hasVisibleNamebool

True if the name is not empty and not the default one.

setAmplitude(amplitude)

Set the amplitude parameter of the spectral density function.

Parameters:
amplitudePoint

The amplitude parameter to be used in the spectral density function.

setName(name)

Accessor to the object’s name.

Parameters:
namestr

The name of the object.

setScale(scale)

Set the scale parameter of the spectral density function.

Parameters:
scalePoint

The scale parameter to be used in the spectral density function. It should be of size dimension.

setShadowedId(id)

Accessor to the object’s shadowed id.

Parameters:
idint

Internal unique identifier.

setVisibility(visible)

Accessor to the object’s visibility state.

Parameters:
visiblebool

Visibility flag.

Examples using the class

Estimate a spectral density function

Estimate a spectral density function

Create a parametric spectral density function

Create a parametric spectral density function

Create a normal process

Create a normal process