DesignProxy¶
- class DesignProxy(*args)¶
Design matrix cache.
- Available constructors:
DesignProxy(x, basis)
DesignProxy(matrix)
- Parameters:
Notes
Helps to cache evaluations of the design matrix. Can be useful for an iterative least squares problem resolution or in interaction with
LeastSquaresMethodto select the algorithm used for the resolution of linear least-squares problems.Examples
>>> import openturns as ot >>> basisSize = 3 >>> sampleSize = 5 >>> X = ot.Sample(sampleSize, 1) >>> X = ot.Sample.BuildFromPoint(range(1, 1 + sampleSize)) >>> phis = [] >>> for j in range(basisSize): ... phis.append(ot.SymbolicFunction(['x'], ['x^' + str(j + 1)])) >>> basis = ot.Basis(phis) >>> proxy = ot.DesignProxy(X, phis)
Methods
computeDesign(indices)Build the design matrix.
getBasis(*args)Accessor to the basis.
Accessor to the object's name.
getId()Accessor to the object's id.
Input sample accessor.
getName()Accessor to the object's name.
Row filter accessor.
Sample size accessor.
Accessor to the object's shadowed id.
Accessor to the object's visibility state.
hasName()Test if the object is named.
Row filter flag accessor.
Test if the object has a distinguishable name.
setName(name)Accessor to the object's name.
setRowFilter(rowFilter)Row filter accessor.
setShadowedId(id)Accessor to the object's shadowed id.
setVisibility(visible)Accessor to the object's visibility state.
- __init__(*args)¶
- computeDesign(indices)¶
Build the design matrix.
- Parameters:
- indicessequence of int
Indices of the current basis in the global basis
- Returns:
- psiAk
Matrix The design matrix
- psiAk
- getBasis(*args)¶
Accessor to the basis.
- Parameters:
- indicessequence of int, optional
Indices of the active functions in the basis
- Returns:
- activeBasisCollection of
Function Collection of functions of the basis associated to the given indices. By default, the whole basis.
- activeBasisCollection of
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getId()¶
Accessor to the object’s id.
- Returns:
- idint
Internal unique identifier.
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getRowFilter()¶
Row filter accessor.
- Returns:
- rowFilter
Indices Sub-indices in of the sample in the current indices
- rowFilter
- getSampleSize()¶
Sample size accessor.
- Returns:
- sampleSizeint
Size of sample accounting for row filter
- getShadowedId()¶
Accessor to the object’s shadowed id.
- Returns:
- idint
Internal unique identifier.
- getVisibility()¶
Accessor to the object’s visibility state.
- Returns:
- visiblebool
Visibility flag.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- hasRowFilter()¶
Row filter flag accessor.
- Returns:
- hasRowFilterbool
Whether sub-indices of the basis are set
- hasVisibleName()¶
Test if the object has a distinguishable name.
- Returns:
- hasVisibleNamebool
True if the name is not empty and not the default one.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setRowFilter(rowFilter)¶
Row filter accessor.
- Parameters:
- rowFiltersequence of int
Sub-indices in of the sample in the current indices
- setShadowedId(id)¶
Accessor to the object’s shadowed id.
- Parameters:
- idint
Internal unique identifier.
- setVisibility(visible)¶
Accessor to the object’s visibility state.
- Parameters:
- visiblebool
Visibility flag.
Examples using the class¶
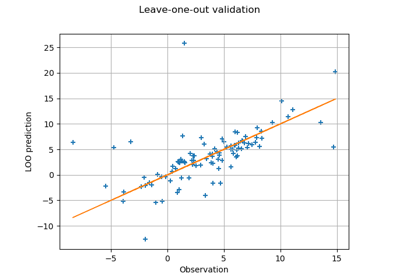
Compute leave-one-out error of a polynomial chaos expansion
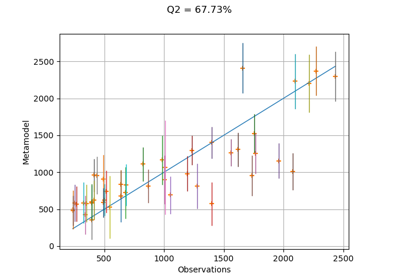
Compute confidence intervals of a regression model from data
 OpenTURNS
OpenTURNS