Note

Go to the end to download the full example code

Create a stationary covariance modelΒΆ

This use case illustrates how the user can define his own stationary covariance model thanks to the object UserDefinedStationaryCovarianceModel defined from:

  • a mesh \mathcal{M} of dimension n defined by the vertices (\underline{\tau}_0,\dots, \underline{\tau}_{N-1}) and the associated simplices,

  • a collection of covariance matrices stored in the object CovarianceMatrixCollection noted \underline{\underline{C}}_0, \dots, \underline{\underline{C}}_{N-1} where \underline{\underline{C}}_k \in \mathcal{M}_{d \times d}(\mathbb{R}) for 0 \leq k \leq N-1

Then we build a stationary covariance function which is a piecewise constant function on \mathcal{D} defined by:

\forall \underline{\tau} \in \mathcal{D}, \, C^{stat}(\underline{\tau}) = \underline{\underline{C}}_k

where k is such that \underline{\tau}_k is the vertex of \mathcal{M} the nearest to \underline{t}.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt

ot.Log.Show(ot.Log.NONE)

We detail the example described in the documentation Create the time grid

t0 = 0.0
dt = 0.5
N = int((20.0 - t0) / dt)
mesh = ot.RegularGrid(t0, dt, N)

# Create the covariance function


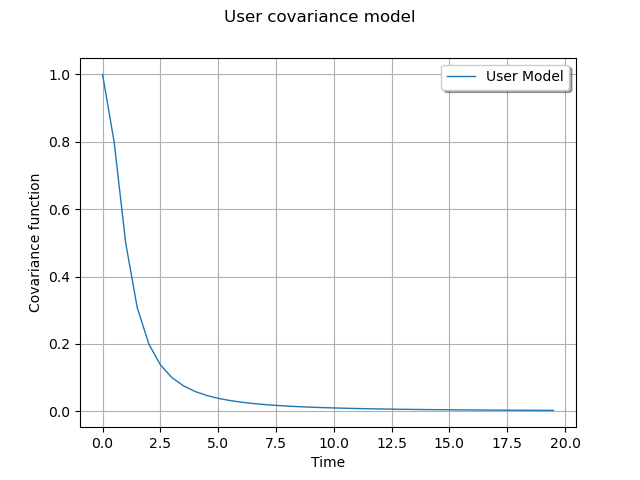
def gamma(tau):
    return 1.0 / (1.0 + tau * tau)


# Create the collection of HermitianMatrix
coll = ot.SquareMatrixCollection()
for k in range(N):
    t = mesh.getValue(k)
    matrix = ot.SquareMatrix([[gamma(t)]])
    coll.add(matrix)

Create the covariance model

covmodel = ot.UserDefinedStationaryCovarianceModel(mesh, coll)

# One vertex of the mesh
tau = 1.5

# Get the covariance function computed at the vertex tau
covmodel(tau)

[[ 0.307692 ]]



Graph of the spectral function

x = ot.Sample(N, 2)
for k in range(N):
    t = mesh.getValue(k)
    x[k, 0] = t
    value = covmodel(t)
    x[k, 1] = value[0, 0]

# Create the curve of the spectral function
curve = ot.Curve(x, "User Model")

# Create the graph
myGraph = ot.Graph("User covariance model", "Time", "Covariance function", True)
myGraph.add(curve)
myGraph.setLegendPosition("upper right")
view = viewer.View(myGraph)
plt.show()
User covariance model