MinimumVolumeClassifier¶

(Source code, png)

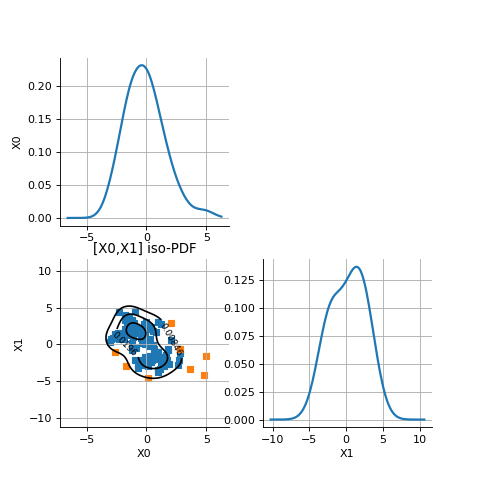
class MinimumVolumeClassifier(*args)¶

Classifier define by a minimum volume level set.

Parameters:

mixtDistDistribution: A distribution.
alphasequence of float, unique and sorted: Confidence levels

Methods

`classify`(*args)	Classify points according to the classifier.
`drawContour`(alpha)	Draw distribution contours.
`drawContourAndSample`(alpha, sample, classes)	Draw distribution contour and classified sample.
`drawSample`(sample, classes)	Draw classified sample.
`getClassName`()	Accessor to the object's name.
`getDimension`()	Accessor to the dimension.
`getDistribution`()	Accessor to the distribution.
`getLevelSet`([j])	LevelSet accessor.
`getName`()	Accessor to the object's name.
`getNumberOfClasses`()	Accessor to the number of classes.
`getThreshold`()	Accessor to the threshold.
`grade`(inP, outC)	Grade points according to the classifier.
`hasName`()	Test if the object is named.
`isParallel`()	Accessor to the parallel flag.
`setName`(name)	Accessor to the object's name.
`setParallel`(flag)	Accessor to the parallel flag.

See also

Classifier

Notes

This implements a mixture classifier which is a particular classifier based on a minimum volume confidence domain.

The minimum volume confidence domain $A^*_{\alpha_i}$ is the set of minimum volume and which measure is at least $\alpha_i$ . It is defined by:

$A^*_{\alpha_i} = \argmin_{A \in \Rset^d\, | \, \mu(A) \geq \alpha_i} \lambda(A)$

where $\lambda$ is the Lebesgue measure on $\Rset^d$ . Under some general conditions on $\mu$ (for example, no flat regions), the set $A^*_{\alpha_i}$ is unique and realises the minimum: $\mu(A^*_{\alpha_i}) = \alpha$ . We show that $A^*_{\alpha_i}$ writes:

$A^*_{\alpha_i} = \{ \vect{x} \in \Rset^d \, | \, p(\vect{x}) \geq p_{\alpha_i} \}$

The classifier proposes 2 classes. The rule to assign a point $\vect{x}$ to a class k is defined as follows: $k = \argmin_i \text{with} p(\vect{x}) > p_{\alpha_i}$

The grade of $\vect{x}$ with respect to the class k is $log p(\vect{x})$ if $\vect{x}$ belongs to class k else $- log p(\vect{x})$ .

Examples

>>> import openturns as ot
>>> R2 = ot.CorrelationMatrix(2)
>>> dists = [ot.Normal([-1.0, 2.0], [1.0]*2, R2), ot.Normal([1.0, -2.0], [1.5]*2, R2)]
>>> mixture = ot.Mixture(dists)
>>> sample = mixture.getSample(1000)
>>> distribution = ot.KernelSmoothing().build(sample)
>>> algo = ot.MinimumVolumeClassifier(distribution, [0.8])
>>> algo.classify(distribution.getMean())
0
>>> algo.classify([100.0]*2)
1
>>> sample = distribution.getSample(100)
>>> graph = algo.drawSample(sample, [0, 1])

__init__(*args)¶

classify(*args)¶

Classify points according to the classifier.

Parameters:

inputsequence of float or 2-d a sequence of float: A point or set of points to classify.

Returns:

clsint or Indices: The class index of the input points, or indices of the classes of each points.

drawContour(alpha)¶

Draw distribution contours.

Parameters:

alphasequence of float: Confidence levels

Returns:

graphGraph: The value of the density function defining the frontier of the domain.

drawContourAndSample(alpha, sample, classes)¶

Draw distribution contour and classified sample.

Parameters:

alphasequence of float: Confidence levels
sampleSample: A sample to classifiy.
classessequence of int: Classes to select

Returns:

graphGraph: The value of the density function defining the frontier of the domain.

drawSample(sample, classes)¶

Draw classified sample.

Parameters:

sampleSample: A sample to classifiy.
classessequence of int: Classes to select

Returns:

graphGraph: The value of the density function defining the frontier of the domain.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getDimension()¶

Accessor to the dimension.

Returns:

dimint: The dimension of the classifier.

getDistribution()¶

Accessor to the distribution.

Returns:

distDistribution: The distribution.

getLevelSet(j=0)¶

LevelSet accessor.

Parameters:

iint: Index

Returns:

levelsetLevelSet: The levelset defining the domain.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getNumberOfClasses()¶

Accessor to the number of classes.

Returns:

n_classesint: The number of classes

getThreshold()¶

Accessor to the threshold.

Returns:

thresholdPoint: The values $p_{\alpha_i}$ of the density function defining the frontier of the domain.

grade(inP, outC)¶

Grade points according to the classifier.

Parameters:

inputPointsequence of float or 2-d a sequence of float: A point or set of points to grade.
kint or sequence of int: The class index, or class indices.

Returns:

gradefloat or Point: Grade or list of grades of each input point with respect to each class index

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

isParallel()¶

Accessor to the parallel flag.

Returns:

flagbool: Logical value telling if the parallel mode has been activated.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setParallel(flag)¶

Accessor to the parallel flag.

Parameters:

flagbool: Logical value telling if the classification and grading are done in parallel.

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

MinimumVolumeClassifier¶