Benchmark the Oakley-O’Hagan test function

import openturns as ot
import otbenchmark as otb
import openturns.viewer as otv

problem = otb.OakleyOHaganSensitivity()
print(problem)

name = Oakley-O'Hagan
distribution = ComposedDistribution(Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), Normal(mu = 0, sigma = 1), IndependentCopula(dimension = 15))
function = class=PythonEvaluation name=OpenTURNSPythonFunction
firstOrderIndices = [0,0,0,0,0,0.02,0.02,0.03,0.05,0.01,0.1,0.14,0.1,0.11,0.12]#15
totalOrderIndices = [0.06,0.06,0.04,0.05,0.02,0.04,0.06,0.08,0.1,0.04,0.15,0.15,0.14,0.14,0.16]#15

distribution = problem.getInputDistribution()
model = problem.getFunction()

Exact first and total order

exact_first_order = problem.getFirstOrderIndices()
print(exact_first_order)

[0,0,0,0,0,0.02,0.02,0.03,0.05,0.01,0.1,0.14,0.1,0.11,0.12]#15

exact_total_order = problem.getTotalOrderIndices()
print(exact_total_order)

[0.06,0.06,0.04,0.05,0.02,0.04,0.06,0.08,0.1,0.04,0.15,0.15,0.14,0.14,0.16]#15

Plot the function

Create X/Y data

ot.RandomGenerator.SetSeed(0)
size = 200
inputDesign = ot.MonteCarloExperiment(distribution, size).generate()
outputDesign = model(inputDesign)

dimension = distribution.getDimension()
nbcolumns = 5
nbrows = int(dimension / nbcolumns)
grid = ot.GridLayout(nbrows, nbcolumns)
inputDescription = distribution.getDescription()
outputDescription = model.getOutputDescription()[0]
index = 0
for i in range(nbrows):
    for j in range(nbcolumns):
        graph = ot.Graph(
            "n=%d" % (size), inputDescription[index], outputDescription, True, ""
        )
        sample = ot.Sample(size, 2)
        sample[:, 0] = inputDesign[:, index]
        sample[:, 1] = outputDesign[:, 0]
        cloud = ot.Cloud(sample)
        graph.add(cloud)
        grid.setGraph(i, j, graph)
        index += 1
_ = otv.View(grid, figure_kw={"figsize": (10.0, 10.0)})

output_distribution = ot.KernelSmoothing().build(outputDesign)
_ = otv.View(output_distribution.drawPDF())

Perform sensitivity analysis

Create X/Y data

ot.RandomGenerator.SetSeed(0)
size = 1000
inputDesign = ot.SobolIndicesExperiment(distribution, size).generate()
outputDesign = model(inputDesign)

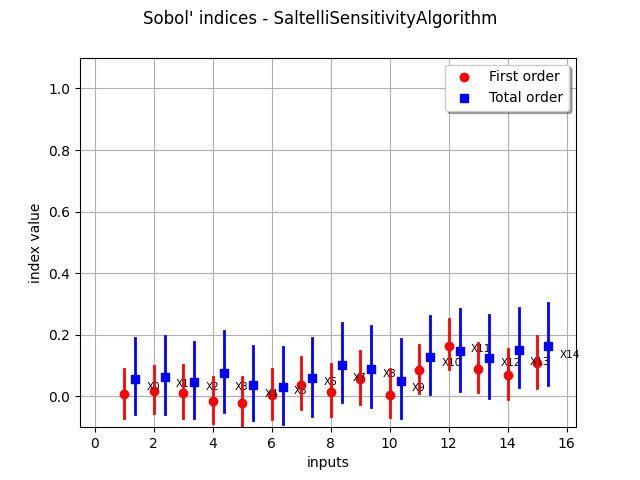
Compute first order indices using the Saltelli estimator

sensitivityAnalysis = ot.SaltelliSensitivityAlgorithm(inputDesign, outputDesign, size)
computed_first_order = sensitivityAnalysis.getFirstOrderIndices()
computed_total_order = sensitivityAnalysis.getTotalOrderIndices()

Compare with exact results

print("Sample size : ", size)
# First order
# Compute absolute error (the LRE cannot be computed,
# because S can be zero)
print("Computed first order = ", computed_first_order)
print("Exact first order = ", exact_first_order)
# Total order
print("Computed total order = ", computed_total_order)
print("Exact total order = ", exact_total_order)

Sample size :  1000
Computed first order =  [-0.0313488,-0.0130586,-0.0203797,-0.0129473,-0.0205151,0.00970655,0.00283849,-0.00230157,0.0261289,-0.0124759,0.109459,0.137281,0.0590927,0.0762443,0.116773]#15
Exact first order =  [0,0,0,0,0,0.02,0.02,0.03,0.05,0.01,0.1,0.14,0.1,0.11,0.12]#15
Computed total order =  [0.0631626,0.0409663,0.0362052,0.0639843,0.0302151,0.0496775,0.0551845,0.08974,0.0999318,0.0331805,0.150836,0.132069,0.14788,0.154901,0.178165]#15
Exact total order =  [0.06,0.06,0.04,0.05,0.02,0.04,0.06,0.08,0.1,0.04,0.15,0.15,0.14,0.14,0.16]#15

_ = otv.View(sensitivityAnalysis.draw())

otv.View.ShowAll()