Convex decomposition

import openturns as ot
import openturns.viewer as otv
import otmeshing

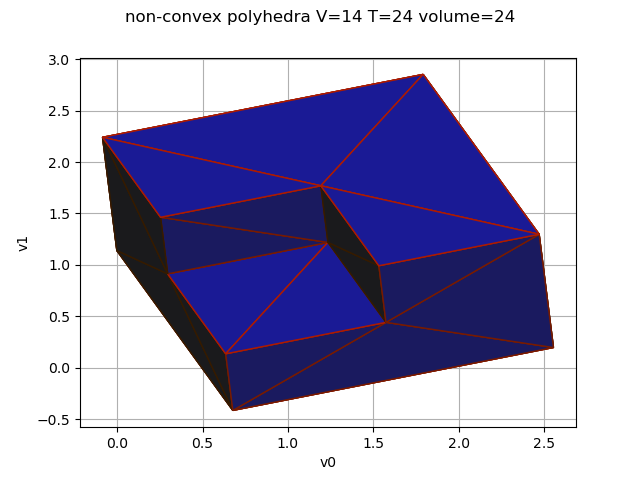
Define a non-convex polyhedra surface mesh: a cube with folded corner

vertices = [
    [0, 0, 0], [2, 0, 0], [2, 2, 0], [0, 2, 0],  # 0–3 bottom
    [0, 0, 2], [2, 0, 2], [0, 2, 2],  # 4–7 top
    [1, 1, 1], [2, 1, 1], [2, 2, 1], [1, 2, 1],  # notch bottom
    [1, 1, 2], [2, 1, 2], [1, 2, 2]]  # notch top
simplices = [
    [0, 1, 5, 5], [0, 5, 4, 4],  # y=0
    [0, 4, 6, 6], [0, 6, 3, 3],  # x=0
    [0, 2, 1, 1], [0, 3, 2, 2],  # z=0
    [10, 9, 2, 2], [10, 2, 3, 3], [10, 3, 6, 6], [10, 6, 13, 13],  # y=2 wall
    [8, 2, 9, 9], [8, 1, 2, 2], [8, 5, 1, 1], [8, 12, 5, 5],  # x=2 wall
    [11, 13, 6, 6], [11, 6, 4, 4], [11, 4, 5, 5], [11, 5, 12, 12],  # z=2 wall
    [8, 7, 12, 12], [7, 11, 12, 12],  # y=1 notch
    [7, 10, 13, 13], [7, 13, 11, 11],  # x=1 notch
    [7, 8, 9, 9], [7, 9, 10, 10]]  # z=1 notch
polyhedra = ot.Mesh(vertices, simplices)

We can check the mesh is not convex

otmeshing.ConvexDecompositionMesher.IsConvex(polyhedra)

False

Draw the polyhedra

shading = True
thetaX, thetaY, thetaZ = 6.1, 3.7, 4.3
drawEdge = True
graph = polyhedra.draw3D(drawEdge, thetaX, thetaY, thetaZ, shading)
V = polyhedra.getVerticesNumber()
T = polyhedra.getSimplicesNumber()
volume = round(polyhedra.getVolume())
graph.setTitle(f"non-convex polyhedra V={V} T={T} volume={volume}")
view = otv.View(graph)

Build the decomposition

mesher = otmeshing.ConvexDecompositionMesher()
decomposition = mesher.build(polyhedra)
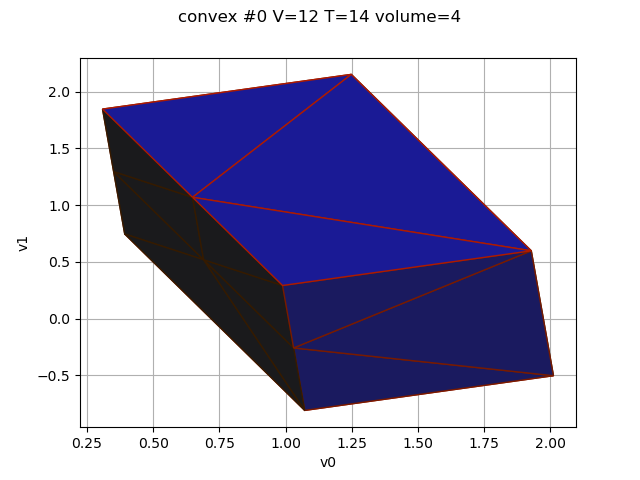
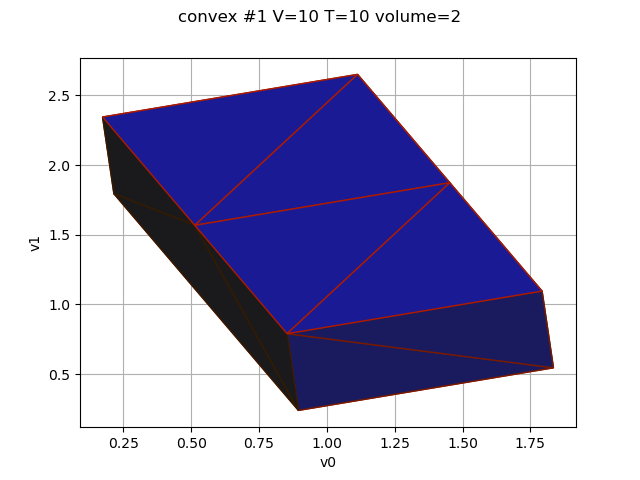
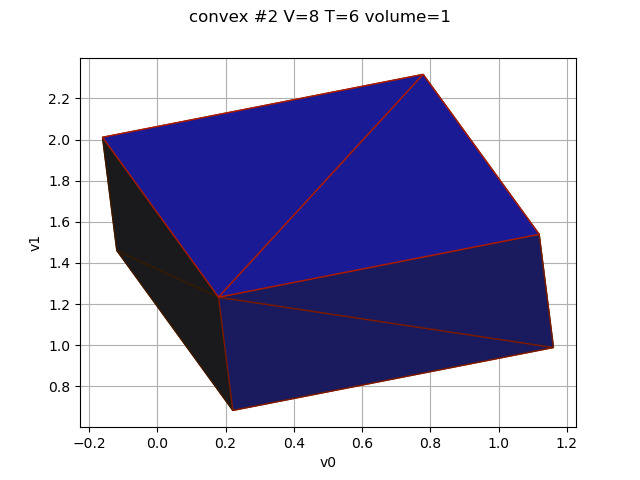
for i, convex in enumerate(decomposition):
    V = convex.getVerticesNumber()
    T = convex.getSimplicesNumber()
    volume = round(convex.getVolume())
    graph = convex.draw3D(drawEdge, thetaX, thetaY, thetaZ, shading)
    graph.setTitle(f"convex #{i} V={V} T={T} volume={volume}")
    view = otv.View(graph)

• 
• 
• 

otv.View.ShowAll()