Note
Go to the end to download the full example code.
Distribution of estimators in linear regression¶
Introduction¶
In this example, we are interested in the distribution of the estimator of the variance
of the observation error in linear regression.
We are also interested in the estimator of the standard deviation of the
observation error.
We show how to use the PythonRandomVector class in order to
perform a study of the sample distribution of these estimators.
In the general linear regression model, the observation error has the
normal distribution
where
is the standard deviation.
We are interested in the estimators of the variance
and the standard deviation
:
the variance of the residuals,
, is estimated from
getResidualsVariance();the standard deviation
is estimated from
getResidualsStandardError().
The asymptotic distribution of these estimators is known (see [vaart2000])
but we want to perform an empirical study, based on simulation.
In order to see the distribution of the estimator, we simulate an observation of the estimator,
and repeat that experiment times, where
is a large integer.
Then we approximate the distribution using
KernelSmoothing.
import openturns as ot
import openturns.viewer as otv
import pylab as pl
The simulation engine¶
The simulation is based on the PythonRandomVector class,
which simulates independent observations of a random vector.
The getRealization() method implements the simulation of the observation
of the estimator.
class SampleEstimatorLinearRegression(ot.PythonRandomVector):
def __init__(
self, sample_size, true_standard_deviation, coefficients, estimator="variance"
):
"""
Create a RandomVector for an estimator from a linear regression model.
Parameters
----------
sample_size : int
The sample size n.
true_standard_deviation : float
The standard deviation of the Gaussian observation error.
coefficients: sequence of p floats
The coefficients of the linear model.
estimator: str
The estimator.
Available estimators are "variance" or "standard-deviation".
"""
super(SampleEstimatorLinearRegression, self).__init__(1)
self.sample_size = sample_size
self.numberOfParameters = coefficients.getDimension()
input_dimension = self.numberOfParameters - 1 # Because of the intercept
centerCoefficient = [0.0] * input_dimension
constantCoefficient = [coefficients[0]]
linearCoefficient = ot.Matrix([coefficients[1:]])
self.linearModel = ot.LinearFunction(
centerCoefficient, constantCoefficient, linearCoefficient
)
self.distribution = ot.Normal(input_dimension)
self.distribution.setDescription(["x%d" % (i) for i in range(input_dimension)])
self.errorDistribution = ot.Normal(0.0, true_standard_deviation)
self.estimator = estimator
# In classical linear regression, the input is deterministic.
# Here, we set it once and for all.
self.input_sample = self.distribution.getSample(self.sample_size)
self.output_sample = self.linearModel(self.input_sample)
def getRealization(self):
errorSample = self.errorDistribution.getSample(self.sample_size)
noisy_output_sample = self.output_sample + errorSample
algo = ot.LinearModelAlgorithm(self.input_sample, noisy_output_sample)
lmResult = algo.getResult()
if self.estimator == "variance":
output = lmResult.getResidualsVariance()
elif self.estimator == "standard-deviation":
lmAnalysis = ot.LinearModelAnalysis(lmResult)
output = lmAnalysis.getResidualsStandardError()
else:
raise ValueError("Unknown estimator %s" % (self.estimator))
return [output]
def plot_sample_by_kernel_smoothing(
sample_size, true_standard_deviation, coefficients, estimator, repetitions_size
):
"""
Plot the estimated distribution of the biased sample variance from a sample
The method uses Kernel Smoothing with default kernel.
Parameters
----------
repetitions_size : int
The number of repetitions of the experiments.
This is the (children) size of the sample of the biased
sample variance
Returns
-------
graph : ot.Graph
The plot of the PDF of the estimated distribution.
"""
myRV = ot.RandomVector(
SampleEstimatorLinearRegression(
sample_size, true_standard_deviation, coefficients, estimator
)
)
sample_estimator = myRV.getSample(repetitions_size)
if estimator == "variance":
sample_estimator.setDescription([r"$\hat{\sigma}^2$"])
elif estimator == "standard-deviation":
sample_estimator.setDescription([r"$\hat{\sigma}$"])
else:
raise ValueError("Unknown estimator %s" % (estimator))
mean_sample_estimator = sample_estimator.computeMean()
graph = ot.KernelSmoothing().build(sample_estimator).drawPDF()
graph.setLegends(["Sample"])
bb = graph.getBoundingBox()
ylb = bb.getLowerBound()[1]
yub = bb.getUpperBound()[1]
curve = ot.Curve([true_standard_deviation**2] * 2, [ylb, yub])
curve.setLegend("Exact")
curve.setLineWidth(2.0)
graph.add(curve)
graph.setTitle(
"Size = %d, True S.D. = %.4f, Mean = %.4f, Rep. = %d"
% (
sample_size,
true_standard_deviation,
mean_sample_estimator[0],
repetitions_size,
)
)
return graph
Distribution of the variance estimator¶
We first consider the estimation of the variance .
In the next cell, we consider a sample size equal to
with
parameters.
We use
repetitions.
repetitions_size = 1000
true_standard_deviation = 0.1
sample_size = 6
coefficients = ot.Point([3.0, 2.0, -1.0])
estimator = "variance"
view = otv.View(
plot_sample_by_kernel_smoothing(
sample_size, true_standard_deviation, coefficients, estimator, repetitions_size
),
figure_kw={"figsize": (6.0, 3.5)},
)
pl.subplots_adjust(bottom=0.25)
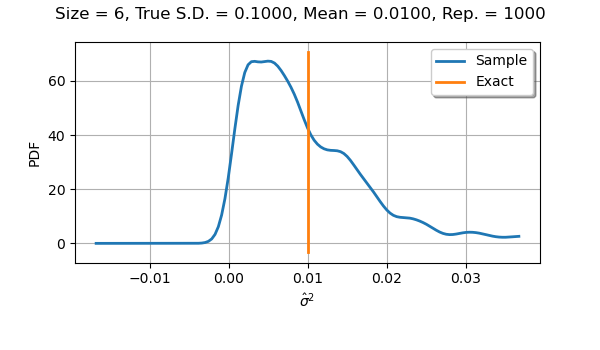
If we use a sample size equal to with
parameters, the distribution is not symmetric.
The mean of the observations of the sample variances remains close to
the true value
.
Then we increase the sample size .
repetitions_size = 1000
true_standard_deviation = 0.1
sample_size = 100
coefficients = ot.Point([3.0, 2.0, -1.0])
view = otv.View(
plot_sample_by_kernel_smoothing(
sample_size, true_standard_deviation, coefficients, estimator, repetitions_size
),
figure_kw={"figsize": (6.0, 3.5)},
)
pl.subplots_adjust(bottom=0.25)
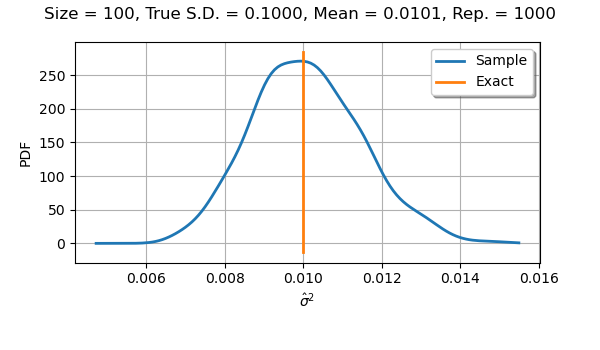
If we use a sample size equal to with
parameters, the distribution is almost symmetric and
almost normal.
Distribution of the standard deviation estimator¶
We now consider the estimation of the standard deviation .
repetitions_size = 1000
true_standard_deviation = 0.1
sample_size = 6
coefficients = ot.Point([3.0, 2.0, -1.0])
estimator = "standard-deviation"
view = otv.View(
plot_sample_by_kernel_smoothing(
sample_size, true_standard_deviation, coefficients, estimator, repetitions_size
),
figure_kw={"figsize": (6.0, 3.5)},
)
pl.subplots_adjust(bottom=0.25)
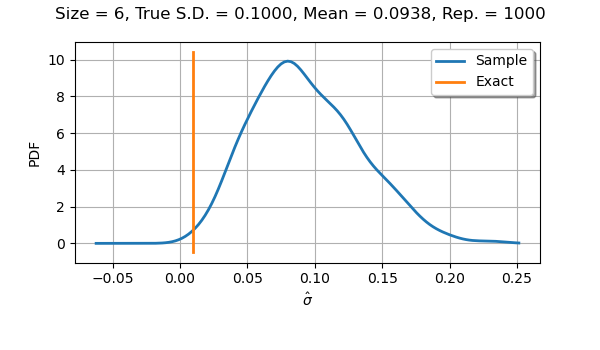
If we use a sample size equal to with
parameters, we see that the distribution is almost symmetric.
We notice a slight bias, since the mean of the observations of the
standard deviation is not as close to the true value 0.1
as we could expect.
repetitions_size = 1000
true_standard_deviation = 0.1
sample_size = 100
coefficients = ot.Point([3.0, 2.0, -1.0])
estimator = "standard-deviation"
view = otv.View(
plot_sample_by_kernel_smoothing(
sample_size, true_standard_deviation, coefficients, estimator, repetitions_size
),
figure_kw={"figsize": (6.0, 3.5)},
)
pl.subplots_adjust(bottom=0.25)
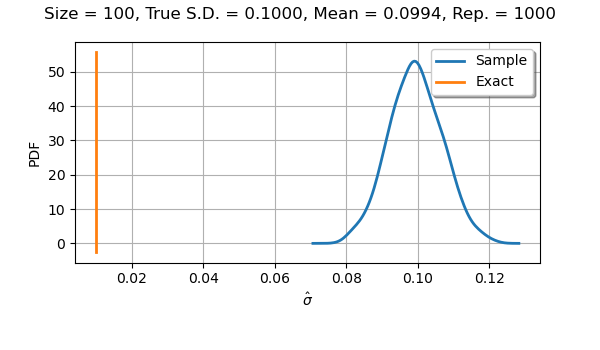
If we use a sample size equal to with
parameters, we see that the distribution is almost normal.
We notice that the bias disappeared.
Total running time of the script: (0 minutes 5.452 seconds)
 OpenTURNS
OpenTURNS