The Chaboche mechanical model

Deterministic model

The Chaboche mechanical law predicts the stress depending on the strain:

\sigma = G(\epsilon,R,C,\gamma) = R + \frac{C}{\gamma} (1-\exp(-\gamma\epsilon))

where:

  • \epsilon is the strain,

  • \sigma is the stress (Pa),

  • R, C, \gamma are the parameters.

The variables have the following distributions and are supposed to be independent.

Random var.

Distribution

R

Lognormal (\mu = 750 MPa, \sigma = 11 MPa)

C

Normal (\mu = 2750 MPa, \sigma = 250 MPa)

\gamma

Normal (\mu = 10, \sigma = 2)

\epsilon

Uniform(a=0, b=0.07).

Thanks to

  • Antoine Dumas, Phimeca

References

    1. Lemaitre and J. L. Chaboche (2002) “Mechanics of solid materials” Cambridge University Press.

API documentation

class ChabocheModel(strainMin=0.0, strainMax=0.07, trueR=750000000.0, trueC=2750000000.0, trueGamma=10.0)

Data class for the Chaboche mechanical model.

Parameters:
strainMinfloat, optional

The minimum value of the strain. The default is 0.0.

strainMaxfloat, optional

The maximum value of the strain. The default is 0.07

trueRfloat, optional

The true value of the R parameter. The default is 750.0e6.

trueCfloat, optional

The true value of the C parameter. The default is 2750.0e6.

trueGammafloat, optional

The true value of the Gamma parameter. The default is 10.0.

Examples

>>> from openturns.usecases import chaboche_model
>>> # Load the Chaboche model
>>> cm = chaboche_model.ChabocheModel()
>>> print(cm.data[:5])
        [ Strain      Stress (Pa) ]
0 : [ 0           7.56e+08    ]
1 : [ 0.0077      7.57e+08    ]
2 : [ 0.0155      7.85e+08    ]
3 : [ 0.0233      8.19e+08    ]
4 : [ 0.0311      8.01e+08    ]
>>> print("Inputs:", cm.model.getInputDescription())
Inputs: [Strain,R,C,Gamma]
>>> print("Outputs:", cm.model.getOutputDescription())
Outputs: [Sigma]
Attributes:
dimThe dimension of the problem

dim=4.

StrainUniform distribution

ot.Uniform(strainMin, strainMax)

RDirac distribution

ot.Dirac(trueR)

CDirac distribution

ot.Dirac(trueC)

GammaDirac distribution

ot.Dirac(trueGamma)

inputDistributionJointDistribution

The joint distribution of the input parameters.

modelPythonFunction

The Chaboche mechanical law. The model has input dimension 4 and output dimension 1. More precisely, we have \vect{X} = (\epsilon, R, C, \gamma) and Y = \sigma.

dataSample of size 10 and dimension 2

A data set which contains noisy observations of the strain (column 0) and the stress (column 1).

Examples based on this use case

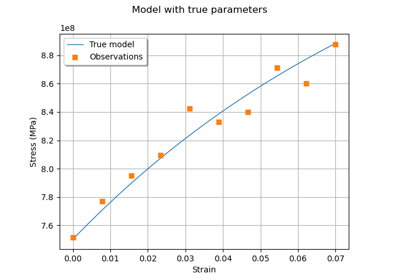
Generate observations of the Chaboche mechanical model

Generate observations of the Chaboche mechanical model

Calibration of the Chaboche mechanical model

Calibration of the Chaboche mechanical model