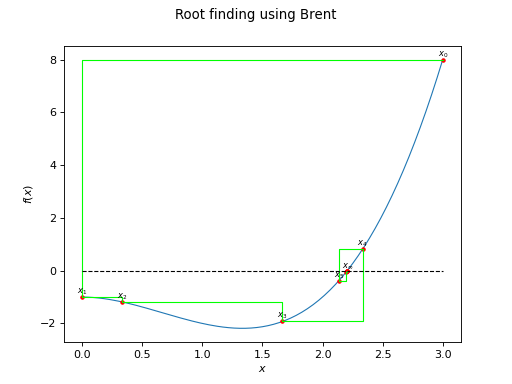
Brent¶

(Source code, png)

class Brent(*args)¶

Brent algorithm solver for 1D non linear equations.

Parameters:

absErrorpositive float, optional: Absolute error: distance between two successive iterates at the end point. Default is $10^{-5}$ .
relErrorpositive float, optional: Relative error: distance between the two last successive iterates with regards to the last iterate. Default is $10^{-5}$ .
resErrorpositive float, optional: Residual error: difference between the last iterate value and the expected value. Default is $10^{-8}$ .
maximumFunctionEvaluationint, optional: The maximum number of evaluations of the function. Default is $100$ .

See also

Solver, Bisection, Secant

Notes

The Brent solver is a mix of Bisection, Secant and inverse quadratic interpolation.

If the function $f$ is continuous, the Brent solver will converge towards a root of the equation $function(x) = value$ in $[infPoint, supPoint]$ . If not, it will converge towards either a root or a discontinuity point of $f$ on $[infPoint, supPoint]$ . Bisection guarantees convergence.

Examples

>>> import openturns as ot
>>> xMin = 0.0
>>> xMax= 3.0
>>> f = ot.MemoizeFunction(ot.SymbolicFunction('x', 'x^3-2*x^2-1'))
>>> solver = ot.Brent()
>>> root = solver.solve(f, 0.0, xMin, xMax)

Methods

`getAbsoluteError`()	Accessor to the absolute error.
`getCallsNumber`()	Accessor to the number of function calls.
`getClassName`()	Accessor to the object's name.
`getMaximumCallsNumber`()	Accessor to the maximum number of function calls.
`getName`()	Accessor to the object's name.
`getRelativeError`()	Accessor to the relative error.
`getResidualError`()	Accessor to the residual error.
`hasName`()	Test if the object is named.
`setAbsoluteError`(absoluteError)	Accessor to the absolute error.
`setMaximumCallsNumber`(maximumFunctionEvaluation)	Accessor to the maximum number of function calls.
`setName`(name)	Accessor to the object's name.
`setRelativeError`(relativeError)	Accessor to the relative error.
`setResidualError`(residualError)	Accessor to the residual error.
`solve`(*args)	Solve an equation.

getMaximumFunctionEvaluation
getUsedFunctionEvaluation
setMaximumFunctionEvaluation

__init__(*args)¶

getAbsoluteError()¶

Accessor to the absolute error.

Returns:

absErrorfloat: The absolute error: distance between two successive iterates at the end point.

getCallsNumber()¶

Accessor to the number of function calls.

Returns:

nEvalint: The number of function calls.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getMaximumCallsNumber()¶

Accessor to the maximum number of function calls.

Returns:

maxEvalint: The maximum number of function calls.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getRelativeError()¶

Accessor to the relative error.

Returns:

relErrorfloat: The relative error: distance between the two last successive iterates with regards to the last iterate.

getResidualError()¶

Accessor to the residual error.

Returns:

resErrorfloat: The residual errors: difference between the last iterate value and the expected value.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

setAbsoluteError(absoluteError)¶

Accessor to the absolute error.

Parameters:

absErrorfloat: The absolute error: distance between two successive iterates at the end point.

setMaximumCallsNumber(maximumFunctionEvaluation)¶

Accessor to the maximum number of function calls.

Parameters:

maxEvalint: The maximum number of function calls.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setRelativeError(relativeError)¶

Accessor to the relative error.

Parameters:

relErrorfloat: The relative error: distance between the two last successive iterates with regards to the last iterate.

setResidualError(residualError)¶

Accessor to the residual error.

Parameters:

resErrorfloat: The residual errors: difference between the last iterate value and the expected value.

solve(*args)¶

Solve an equation.

Parameters:

functionFunction: The function of the equation $function(x) = value$ to be solved in the interval $[infPoint, supPoint]$ .
valuefloat: The value to which the function must be equal.
infPoint, supPointfloat: Lower and upper bounds of the variable $x$ range.
infValue, supValuefloat, optional: The values such that $infValue = function(infPoint)$ , and $supValue = function(supPoint)$ . $infValue$ must be of opposite sign of $supValue$ .

Returns: