Kolmogorov¶
- Kolmogorov(sample, distribution, level=0.05)¶
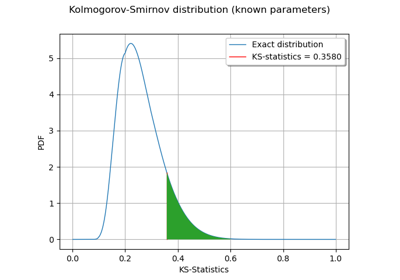
Perform a Kolmogorov goodness-of-fit test for 1-d continuous distributions.
Refer to The Kolmogorov-Smirnov goodness of fit test for continuous data.
- Parameters:
- sample2-d sequence of float
Tested sample.
- model
Distribution. - levelfloat,
, optional (default level = 0.05).
This is the risk
of committing a Type I error, that is an incorrect rejection of a true null hypothesis.
- Returns:
- test_result
TestResult Test result.
- test_result
- Raises:
- TypeError
If the distribution is not continuous or if the sample is multivariate.
Notes
The distribution is supposed to be fully specified, i.e. no parameter has been estimated from the given sample. The implementation of the Kolmogorov cumulative distribution function follows the algorithm described in [simard2011].
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> distribution = ot.Normal() >>> sample = distribution.getSample(30) >>> test_result = ot.FittingTest.Kolmogorov(sample, distribution) >>> test_result class=TestResult name=Unnamed type=Kolmogorov Normal binaryQualityMeasure=true p-value threshold=0.05 p-value=0.970418 statistic=0.0845532 description=[Normal(mu = 0, sigma = 1) vs sample Normal]
We set the level of the Kolmogorov-Smirnov test to 0.01. This parameter value rejects a sample less often than the default value 0.05.
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> distribution = ot.Normal() >>> sample = distribution.getSample(30) >>> level = 0.01 >>> test_result = ot.FittingTest.Kolmogorov(sample, distribution, level)
 OpenTURNS
OpenTURNS