StudentFactory

(Source code, png)

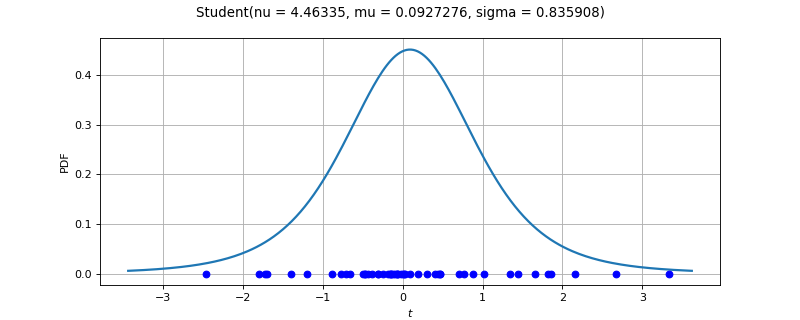
../../_images/openturns-StudentFactory-1.png
class StudentFactory(*args)

Student factory.

See also

DistributionFactory, Student

Notes

Some parameters are estimated by the method of moments and others by the maximum reduced likelihood method:

\begin{align*} \Hat{\mu} = &\Hat{\mu}_x \\ \Hat{\sigma} = &\Hat{\sigma}_x\sqrt{\dfrac{\Hat{\nu}-2}{\Hat{\nu}}} \\ \Hat{R}_{ij} = &\dfrac{2}{\pi}\arcsin(\tau_{ij}) \end{align*}

where \mat{\tau} is the sample Kendall tau matrix and \Hat{\nu} maximizes the reduced likelihood associated to Student with parameters (\Hat{\nu}, \Hat{\mu}, \hat{\sigma}(\Hat{\nu}), \Hat{\mat{R}}).

Methods

build(*args)

Build the distribution.

buildAsStudent(*args)

Estimate the distribution as native distribution.

buildEstimator(*args)

Build the distribution and the parameter distribution.

getBootstrapSize()

Accessor to the bootstrap size.

getClassName()

Accessor to the object's name.

getName()

Accessor to the object's name.

hasName()

Test if the object is named.

setBootstrapSize(bootstrapSize)

Accessor to the bootstrap size.

setName(name)

Accessor to the object's name.
__init__(*args)
build(*args)

Build the distribution.

Available usages:

build()

build(sample)

build(param)

Parameters:
sample2-d sequence of float

Data.

paramsequence of float

The parameters of the distribution.

Returns:
distDistribution

The estimated distribution.

In the first usage, the default native distribution is built.

buildAsStudent(*args)

Estimate the distribution as native distribution.

Available usages:

buildAsStudent()

buildAsStudent(sample)

buildAsStudent(param)

Parameters:
sample2-d sequence of float

Data.

paramsequence of float

The parameters of the Student.

Returns:
distStudent

The estimated distribution as a Student.

In the first usage, the default Student distribution is built.

buildEstimator(*args)

Build the distribution and the parameter distribution.

Parameters:
sample2-d sequence of float

Data.

parametersDistributionParameters

Optional, the parametrization.

Returns:
resDistDistributionFactoryResult

The results.

Notes

According to the way the native parameters of the distribution are estimated, the parameters distribution differs:

  • Moments method: the asymptotic parameters distribution is normal and estimated by Bootstrap on the initial data;

  • Maximum likelihood method with a regular model: the asymptotic parameters distribution is normal and its covariance matrix is the inverse Fisher information matrix;

  • Other methods: the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting (see KernelSmoothing).

If another set of parameters is specified, the native parameters distribution is first estimated and the new distribution is determined from it:

  • if the native parameters distribution is normal and the transformation regular at the estimated parameters values: the asymptotic parameters distribution is normal and its covariance matrix determined from the inverse Fisher information matrix of the native parameters and the transformation;

  • in the other cases, the asymptotic parameters distribution is estimated by Bootstrap on the initial data and kernel fitting.

getBootstrapSize()

Accessor to the bootstrap size.

Returns:
sizeint

Size of the bootstrap.

getClassName()

Accessor to the object’s name.

Returns:
class_namestr

The object class name (object.__class__.__name__).

getName()

Accessor to the object’s name.

Returns:
namestr

The name of the object.

hasName()

Test if the object is named.

Returns:
hasNamebool

True if the name is not empty.

setBootstrapSize(bootstrapSize)

Accessor to the bootstrap size.

Parameters:
sizeint

The size of the bootstrap.

setName(name)

Accessor to the object’s name.

Parameters:
namestr

The name of the object.

Examples using the class

Fit a parametric distribution

Fit a parametric distribution