Strong Maximum Test¶

The Strong Maximum Test is used under the following context: let $\inputRV$ be a probabilistic input vector with joint density probability $\pdf$ , let $\model$ be the limit state function of the model and let $\cD_f = \{\vect{x} \in \Rset^\inputDim \, / \, \model(\vect{x}) \le 0\}$ be an event whose probability $P_f$ is defined as:

(1)¶ $P_f = \int_{{\model(\inputRV) \le 0}} \pdf\, d\vect{x}$

The probability $P_f$ is evaluated with the FORM and SORM methods. These methods use the Nataf isoprobabilistic transformation which maps the probabilistic model in terms of $\inputRV$ onto an equivalent model in terms of $n$ independent standard normal random $\vect{U}$ (refer to Isoprobabilistic transformations). In that new $\vect{u}$ -space, the event has the new expression defined from the transformed limit state function of the model $G$ : $\cD_f = \{\vect{U} \in \Rset^d \, / \, h(\vect{U}) \le 0\}$ .

These analytical methods rely on the assumption that most of the contribution to $P_f$ comes from points located in the vicinity of a particular point $P^*$ , the design point, defined in the $\vect{u}$ -space as the point located on the limit state surface and of maximal likelihood. Given the probabilistic characteristics of the $\vect{u}$ -space, $P^*$ has a geometrical interpretation : it is the point located on the event boundary and at minimal distance from the center of the $\vect{u}$ -space. Thus, the design point $P^*$ is the result of a constrained optimization problem.

Both FORM and SORM methods assume that $P^*$ is unique. One important difficulty comes from the fact that numerical methods involved in the determination of $P^*$ gives no guaranty of a global optimum: the point to which they converge might be a local optimum only. In that case, the contribution of the points in the vicinity of the real design point is not taken into account, and this contribution is the most important one.

Furthermore, even in the case where the global optimum has really been found, there may exist another local optimum $\tilde{P}^*$ with likelihood only slightly inferior to the likelihood of the design point one, which means that it is only slightly further apart from the center of the $\vect{u}$ -space than the design point. Thus, points in the vicinity of $\tilde{P}^*$ may contribute significantly to the probability $P_f$ and are not taken into account in the FORM and SORM approximations.

In both cases, the FORM and SORM approximations are of bad quality because they neglect important contributions to $P_f$ . The Strong Maximum Test helps to evaluate the quality of the design point resulting from the optimization algorithm. It checks whether the design point computed is:

the true design point, which means a global maximum point,
a strong design point, which means that there is no other local maximum located on the event boundary and with likelihood only slightly inferior to the likelihood of the design point one.

This verification is very important in order to give sense to the FORM and SORM approximations.

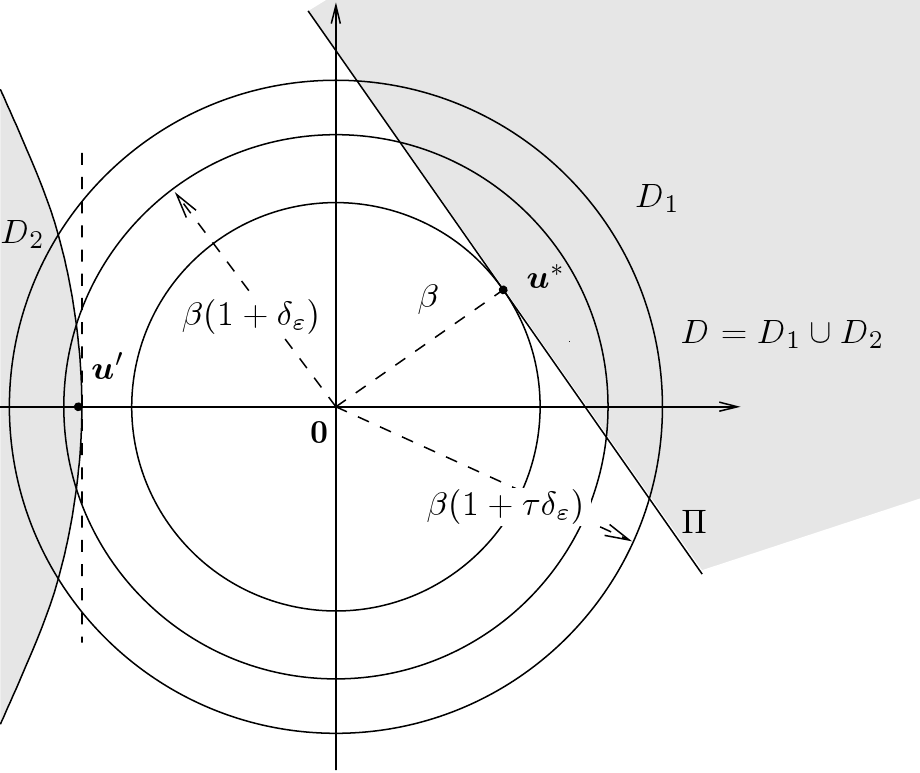
The principle of the Strong Maximum Test relies on the geometrical definition of the design point. The objective is to detect all the points $\tilde{P}^*$ in the ball of radius $R_{\varepsilon} = \beta(1+\delta_{\varepsilon})$ which are potentially the real design point (case of $\tilde{P}_2^*$ ) or whose contribution to $P_f$ is not negligible as regards the approximations Form and SORM (case of $\tilde{P}_1^*$ ). The contribution of a point is considered as negligible when its likelihood in the $\vect{u}$ -space is less than $\varepsilon$ times the likelihood of the design point. The radius $R_{\varepsilon}$ is the distance to the $\vect{u}$ -space center upon which points are considered as negligible $P_f$ .

In order to catch the potential points located on the sphere of radius $R_{\varepsilon}$ (frontier of the zone of prospection), it is necessary to go a little further : this is why the test samples the sphere of radius $R = \beta(1+\tau \delta_{\varepsilon})$ , with $\tau >0$ .

Points on the sampled sphere which are in the vicinity of the design point $P^*$ are less interesting than those verifying the event and located far from the design point : the latter might reveal a potential $\tilde{P}^*$ whose contribution to $P_f$ has to be taken into account. The vicinity of the design point is defined with the angular parameter $\alpha$ as the cone centered on $P^*$ and of half-angle $\alpha$ .

The number $N$ of the simulations sampling the sphere of radius $R$ is determined to ensure that the test detects with a probability greater than $(1 - q)$ any point verifying the event and outside the design point vicinity.

The vicinity of the design point is the arc of the sampled sphere which is inside the half space whose frontier is the linearized limit state function at the Design Point: the vicinity is the arc included in the half space $D_1$ .

../../_images/StrongMaxTest_vicinity.png

The Strong Maximum Test proceeds as follows. The User selects the parameters:

the importance level $\varepsilon$ , where $0 < \varepsilon < 1$ ,
the accuracy level $\tau$ , where $\tau >0$ ,
the confidence level $(1 - q)$ where $0<q<1$ or the number of points $N$ used to sample the sphere. The parameters are deductible from one other.

The Strong Maximum Test will sample the sphere of radius $\beta(1+\tau \delta_{\varepsilon})$ , where $\delta_{\varepsilon} = \sqrt{1 - 2 \frac{\ln(\varepsilon)}{\beta^2}}- 1$ .

The test will detect with probability greater than $(1 - q)$ any point of $\cD_f$ whose contribution to $P_f$ is not negligible (i.e. with density value in the $\vect{u}$ -space greater than $\varepsilon$ times the density value at the design point).

The Strong Maximum Test provides:

set 1: all the points detected on the sampled sphere that are in $\cD_f$ and outside the design point vicinity, with the corresponding value of the limit state function,
set 2: all the points detected on the sampled sphere that are in $\cD_f$ and in the design point vicinity, with the corresponding value of the limit state function,
set 3: all the points detected on the sampled sphere that are outside $\cD_f$ and outside the design point vicinity, with the corresponding value of the limit state function,
set 4: all the points detected on the sampled sphere that are outside $\cD_f$ but in the vicinity of the design point, with the corresponding value of the limit state function.

Points are described by their coordinates in the $\vect{x}$ -space.

The parameter $\tau$ is directly linked to the hypothesis according to which the boundary of the space $\cD_f$ is supposed to be well approximated by a plane near the design point, which is primordial for a FORM approximation of the probability content of $\cD_f$ . Increasing $\tau$ is increasing the area where the approximation FORM is applied.

The parameter $\tau$ also serves as a measure of distance from the design point $P^*$ for a hypothetical local maximum: the larger it is, the further we search for another local maximum. Numerical experiments show that it is recommended to take $\tau \leq 4$ (see the given reference below).

The following table helps to quantify the parameters of the test for a problem of dimension 5.

$\beta_g$	$\varepsilon$	$\tau$	$1-q$	$\delta_{\varepsilon}$	$N$
3.0	0.01	2.0	0.9	$4.224 e^{-1}$	62
3.0	0.01	2.0	0.99	$4.224 e^{-1}$	124
3.0	0.01	4.0	0.9	$4.224 e^{-1}$	15
3.0	0.01	4.0	0.99	$4.224 e^{-1}$	30
3.0	0.1	2.0	0.9	$2.295 e^{-1}$	130
3.0	0.1	2.0	0.99	$2.295 e^{-1}$	260
3.0	0.1	4.0	0.9	$2.295 e^{-1}$	26
3.0	0.1	4.0	0.99	$2.295 e^{-1}$	52
5.0	0.01	2.0	0.9	$1.698 e^{-1}$	198
5.0	0.01	2.0	0.99	$1.698 e^{-1}$	397
5.0	0.01	4.0	0.9	$1.698 e^{-1}$	36
5.0	0.01	4.0	0.99	$1.698 e^{-1}$	72
5.0	0.1	2.0	0.9	$8.821 e^{-2}$	559
5.0	0.1	2.0	0.99	$8.821 e^{-2}$	1118
5.0	0.1	4.0	0.9	$8.821 e^{-2}$	85
5.0	0.1	4.0	0.99	$8.821 e^{-2}$	169

$\beta_g$	$\varepsilon$	$\tau$	$N$	$\delta_{\varepsilon}$	$1-q$
3.0	0.01	2.0	100	$4.224e^{-1}$	0.97
3.0	0.01	2.0	1000	$4.224e^{-1}$	1.0
3.0	0.01	4.0	100	$4.224e^{-1}$	1.0
3.0	0.01	4.0	1000	$4.224e^{-1}$	1.0
3.0	0.1	2.0	100	$2.295e^{-1}$	0.83
3.0	0.1	2.0	1000	$2.295e^{-1}$	1.0
3.0	0.1	4.0	100	$2.295e^{-1}$	1.0
3.0	0.1	4.0	1000	$2.295e^{-1}$	1.0
5.0	0.01	2.0	100	$1.698e^{-1}$	0.69
5.0	0.01	2.0	1000	$1.698e^{-1}$	1.0
5.0	0.01	4.0	100	$1.698e^{-1}$	1.0
5.0	0.01	4.0	1000	$1.698e^{-1}$	1.0
5.0	0.1	2.0	100	$8.821 e^{-2}$	0.34
5.0	0.1	2.0	1000	$8.821 e^{-2}$	0.98
5.0	0.1	4.0	100	$8.821 e^{-2}$	0.93
5.0	0.1	4.0	1000	$8.821 e^{-2}$	0.99

As the Strong Maximum Test involves the computation of $N$ values of the limit state function, which is computationally intensive, it is interesting to have more than just an indication about the quality of $P^*$ . In fact, the test gives some information about the trace of the limit state function on the sphere of radius $\beta(1+\tau \delta_{\varepsilon})$ centered on the origin of the $\vect{u}$ -space. Two cases can be distinguished:

Case 1: set 1 is empty. We are confident on the fact that $P^*$ is a design point verifying the hypothesis according to which most of the contribution of $P_f$ is concentrated in the vicinity of $P^*$ . By using the value of the limit state function on the sample $(\vect{U}_1, \dots, \vect{U}_N)$ , we can check if the limit state function is reasonably linear in the vicinity of $P^*$ , which can validate the second hypothesis of FORM.

If the behavior of the limit state function is not linear, we can decide to use an importance sampling version of the Monte Carlo method to compute the probability of failure. However, the information obtained through the Strong Max Test, according to which $P^*$ is the actual design point, is quite essential : it allows one to construct an effective importance sampling density, e.g. a multidimensional Gaussian distribution centered on $P^*$ .
Case 2: set 1 is not empty. There are two possibilities:
1. We have found some points that suggest that $P^*$ is not a strong maximum, because for some points of the sampled sphere, the value taken by the limit state function is slightly negative;
2. We have found some points that suggest that $P^*$
  is not even the global maximum, because for some points of the sampled sphere, the value taken by the limit state function is very negative. In the first case, we can decide to use an importance sampling version of the Monte Carlo method for computing the probability of failure, but with a mixture of e.g. multidimensional gaussian distributions centered on the $U_i$ in $\cD_f$ (refer to ). In the second case, we can restart the search of the design point by starting at the detected $U_i$ .

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

Strong Maximum Test¶