FORM¶
- class FORM(*args)¶
First Order Reliability Method (FORM).
Refer to FORM.
- Parameters:
- nearestPointAlgorithm
OptimizationAlgorithm Optimization algorithm used to search the design point.
- event
RandomVector Failure event.
- physicalStartingPointsequence of float
Starting point of the optimization algorithm, declared in the physical space.
- nearestPointAlgorithm
Methods
Accessor to the result.
Accessor to the object's name.
getEvent()Accessor to the event of which the probability is calculated.
getName()Accessor to the object's name.
Accessor to the optimization algorithm used to find the design point.
Accessor to the starting point of the optimization algorithm.
Accessor to the result of FORM.
hasName()Test if the object is named.
run()Evaluate the failure probability.
setEvent(event)Accessor to the event of which the probability is calculated.
setName(name)Accessor to the object's name.
setNearestPointAlgorithm(solver)Accessor to the optimization algorithm used to find the design point.
setPhysicalStartingPoint(physicalStartingPoint)Accessor to the starting point of the optimization algorithm.
setResult(formResult)Accessor to the result of FORM.
See also
Notes
See
Analyticalfor the description of the first steps of the FORM analysis.The First Order Reliability Method (FORM) consists in linearizing the limit state function
at the design point, denoted
, which is the point on the limit state surface
that is closest to the origin of the standard space.
Then, the probability
where the limit state surface has been approximated by a linear surface (hyperplane) can be obtained exactly, thanks to the rotation invariance of the standard distribution
:
where
is the Hasofer-Lind reliability index, defined as the distance of the design point
to the origin of the standard space and
the marginal cumulative distribution function of the spherical distributions in the standard space.
The evaluation of the failure probability is stored in the data structure
FORMResultrecoverable with thegetResult()method.Examples
>>> import openturns as ot >>> myFunction = ot.SymbolicFunction(['E', 'F', 'L', 'I'], ['-F*L^3/(3*E*I)']) >>> myDistribution = ot.Normal([50.0, 1.0, 10.0, 5.0], [1.0]*4, ot.IdentityMatrix(4)) >>> vect = ot.RandomVector(myDistribution) >>> output = ot.CompositeRandomVector(myFunction, vect) >>> event = ot.ThresholdEvent(output, ot.Less(), -3.0) >>> # We create an OptimizationAlgorithm algorithm >>> solver = ot.AbdoRackwitz() >>> algo = ot.FORM(solver, event, [50.0, 1.0, 10.0, 5.0]) >>> algo.run() >>> result = algo.getResult()
- __init__(*args)¶
- getAnalyticalResult()¶
Accessor to the result.
- Returns:
- result
AnalyticalResult Result structure which contains the results of the optimisation problem.
- result
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getEvent()¶
Accessor to the event of which the probability is calculated.
- Returns:
- event
RandomVector Event of which the probability is calculated.
- event
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getNearestPointAlgorithm()¶
Accessor to the optimization algorithm used to find the design point.
- Returns:
- algorithm
OptimizationAlgorithm Optimization algorithm used to research the design point.
- algorithm
- getPhysicalStartingPoint()¶
Accessor to the starting point of the optimization algorithm.
- Returns:
- point
Point Starting point of the optimization algorithm, declared in the physical space.
- point
- getResult()¶
Accessor to the result of FORM.
- Returns:
- result
FORMResult Structure containing all the results of the FORM analysis.
- result
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- run()¶
Evaluate the failure probability.
Notes
Evaluate the failure probability and create a
FORMResult, the structure result which is accessible with the methodgetResult().
- setEvent(event)¶
Accessor to the event of which the probability is calculated.
- Parameters:
- event
RandomVector Event of which the probability is calculated.
- event
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setNearestPointAlgorithm(solver)¶
Accessor to the optimization algorithm used to find the design point.
- Parameters:
- algorithm
OptimizationAlgorithm Optimization algorithm used to research the design point.
- algorithm
- setPhysicalStartingPoint(physicalStartingPoint)¶
Accessor to the starting point of the optimization algorithm.
- Parameters:
- pointsequence of float
Starting point of the optimization algorithm, declared in the physical space.
- setResult(formResult)¶
Accessor to the result of FORM.
- Parameters:
- result
FORMResult Structure containing all the results of the FORM analysis.
- result
Examples using the class¶

Use the post-analytical importance sampling algorithm
Use the FORM algorithm in case of several design points

Test the design point with the Strong Maximum Test
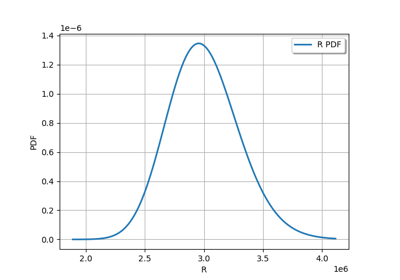
Axial stressed beam : comparing different methods to estimate a probability
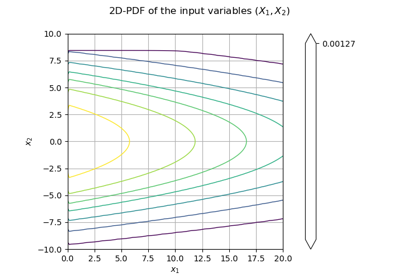
An illustrated example of a FORM probability estimate
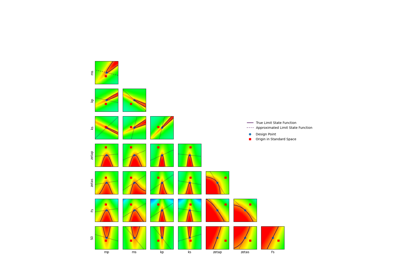
Using the FORM - SORM algorithms on a nonlinear function
 OpenTURNS
OpenTURNS