TaylorExpansionMoments¶
- class TaylorExpansionMoments(*args)¶
Moments approximations from Taylor expansions.
- Parameters:
- limitStateVariable
RandomVector It must be of type Composite, which means it must have been defined with the class
CompositeRandomVector.
- limitStateVariable
Methods
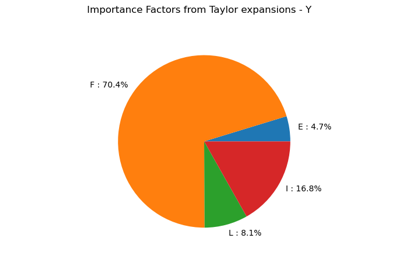
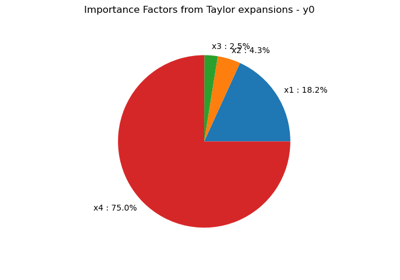
Draw the importance factors.
Accessor to the object's name.
Get the approximation of the covariance matrix.
Get the gradient of the function at the mean point.
Get the hessian of the function.
Get the importance factors.
Get the limit state variable.
Get the first-order approximation of the mean.
Get the second-order approximation of the mean.
getName()Accessor to the object's name.
Get the value of the function at the mean point.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
Notes
Assuming that
has finite first and second order moments and that
is sufficiently smooth, a Taylor expansion of the function
is used to approximate the mean and variance of the random vector
.
Refer to Refer to Taylor Expansion Moments for details on the expressions of the approximations:
the first-order expansion of
yields an approximation of the mean and the variance of
;
the second-order expansion of
yields an approximation of the mean
.
Refer to Taylor Importance Factors for details on the importance factors of each input on the output.
Examples
>>> import openturns as ot >>> ot.RandomGenerator.SetSeed(0) >>> myFunc = ot.SymbolicFunction(['x1', 'x2', 'x3', 'x4'], ... ['(x1*x1+x2^3*x1)/(2*x3*x3+x4^4+1)', 'cos(x2*x2+x4)/(x1*x1+1+x3^4)']) >>> R = ot.CorrelationMatrix(4) >>> for i in range(4): ... R[i, i - 1] = 0.25 >>> distribution = ot.Normal([0.2]*4, [0.1, 0.2, 0.3, 0.4], R) >>> # We create a distribution-based RandomVector >>> X = ot.RandomVector(distribution) >>> # We create a composite RandomVector Y from X and myFunc >>> Y = ot.CompositeRandomVector(myFunc, X) >>> # We create a Taylor expansion method to approximate moments >>> myTaylorExpansionMoments = ot.TaylorExpansionMoments(Y) >>> print(myTaylorExpansionMoments.getMeanFirstOrder()) [0.0384615,0.932544]
- __init__(*args)¶
- drawImportanceFactors()¶
Draw the importance factors.
- Returns:
- graph
Graph Pie graph of the importance factors.
- graph
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getCovariance()¶
Get the approximation of the covariance matrix.
- Returns:
- covariance
CovarianceMatrix Approximation of the covariance matrix from the first-order Taylor expansion.
- covariance
- getGradientAtMean()¶
Get the gradient of the function at the mean point.
- Returns:
- gradient
Matrix Gradient of
at the mean point of the input random vector.
- gradient
- getHessianAtMean()¶
Get the hessian of the function.
- Returns:
- hessian
SymmetricTensor Hessian of the Function which defines the random vector at the mean point of the input random vector.
- hessian
- getImportanceFactors()¶
Get the importance factors.
- Returns:
- factors
Point Importance factors of the inputs : only when randVect is of dimension 1.
- factors
- getLimitStateVariable()¶
Get the limit state variable.
- Returns:
- limitStateVariable
RandomVector The
output random vector.
- limitStateVariable
- getMeanFirstOrder()¶
Get the first-order approximation of the mean.
- Returns:
- mean
Point Approximation of
from the first-order Taylor expansion.
- mean
- getMeanSecondOrder()¶
Get the second-order approximation of the mean.
- Returns:
- mean
Point Approximation of
from the second-order Taylor expansion.
- mean
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
Example of sensitivity analyses on the wing weight model
 OpenTURNS
OpenTURNS