TrendFactory

(Source code, png)

../../_images/TrendFactory.png
class TrendFactory(*args)

Trend estimator.

Refer to Trend computation.

Parameters:
basisSequenceFactoryBasisSequenceFactory

The regression strategy that provides the estimation of the coefficients associated to the best model among the basis functions.

Default is the least angle regression (LARS) method for the choice of sparse models: LARS.

fittingAlgorithmFittingAlgorithm, optional

The fitting algorithm that estimates the empirical error on each sub-basis.

Default is the leave one out strategy: CorrectedLeaveOneOut.

Methods

build(field, basis)

Estimate the trend of a process.

getBasisSequenceFactory()

Accessor to functional basis.

getClassName()

Accessor to the object's name.

getFittingAlgorithm()

Accessor to fitting algorithm basis.

getName()

Accessor to the object's name.

hasName()

Test if the object is named.

setBasisSequenceFactory(basisSequenceFactory)

Accessor to functional basis.

setFittingAlgorithm(fittingAlgorithm)

Accessor to fitting algorithm basis.

setName(name)

Accessor to the object's name.

Notes

A multivariate stochastic process X: \Omega \times \cD \rightarrow \Rset^d of dimension d where \cD \in \Rset^n can write as the sum of a trend function f_{trend}: \Rset^n \rightarrow \Rset^d and a stationary multivariate stochastic process X_{stat}: \Omega \times \cD \rightarrow \Rset^d of dimension d as follows:

X(\omega,\vect{t}) = X_{stat}(\omega,\vect{t}) + f_{trend}(\vect{t})

The TrendFactory enables to identify the trend function f_{trend} from a given field of the process X and then to remove this last one from the initial field. The resulting field is a realization of the process X_{stat}.

We consider the functional basis \cB = (f_1, f_2, \ldots, f_K) with f_j : \Rset^n \longrightarrow \Rset^d. The trend function f_{trend} writes:

f_{trend}(\vect{t}) = \sum_{j=1}^{K} \alpha_j f_j(\vect{t})

The coefficients \alpha_j \in \Rset have to be computed. In the case where the number of available data is of the same order as K, the least square system is ill-posed and a more complex algorithm should be used. Some algorithms combine cross validation techniques and advanced regression strategies, in order to provide the estimation of the coefficients associated to the best model among the basis functions (sparse model). For example, we can use the least angle regression (LARS) method for the choice of sparse models. Then, some fitting algorithms like the leave one out, coupled to the regression strategy, assess the error on the prediction and enable the selection of the best sparse model.

__init__(*args)
build(field, basis)

Estimate the trend of a process.

Available usages:

build(field, basis)

Parameters:
fieldField

One realization of the process.

basisBasis

A collection of functions composing the functional basis.

Returns:
myTrendTransformTrendTransform

The estimated trend function.

Examples

Define a scalar temporal Gaussian process on a mesh of dimension 1:

>>> import openturns as ot
>>> myGrid = ot.RegularGrid(0.0, 1.0, 100)
>>> amplitude=[5.0]
>>> scale=[0.2]
>>> myCovModel=ot.ExponentialModel(scale, amplitude)
>>> myXProcess=ot.GaussianProcess(myCovModel, myGrid)

Create a trend function: f_{trend} : \Rset \mapsto \Rset where f_{trend}(t)=1+2t+t^2:

>>> fTrend = ot.SymbolicFunction(['t'], ['1+2*t+t^2'])
>>> fTemp = ot.TrendTransform(fTrend, myGrid)

Add the trend to the initial process and get a field:

>>> myYProcess = ot.CompositeProcess(fTemp, myXProcess)
>>> myYField = myYProcess.getRealization()

Estimate the trend function from the field:

>>> myBasisSequenceFactory = ot.LARS()
>>> myFittingAlgorithm = ot.KFold()
>>> func1 = ot.SymbolicFunction(['t'], ['1'])
>>> func2 = ot.SymbolicFunction(['t'], ['t'])
>>> func3 = ot.SymbolicFunction(['t'], ['t^2'])
>>> myBasis = ot.Basis([func1, func2, func3])

>>> myTrendFactory = ot.TrendFactory(myBasisSequenceFactory, myFittingAlgorithm)
>>> myTrendTransform =  myTrendFactory.build(myYField, myBasis)

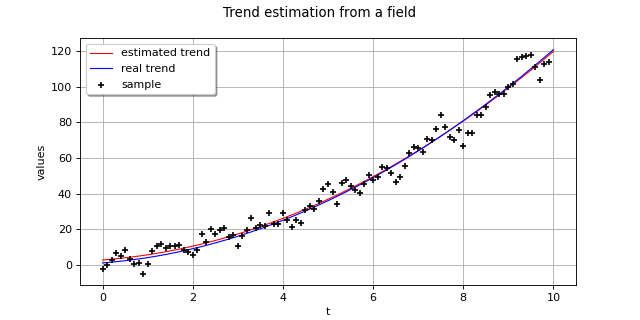
>>> graph = myTrendTransform.getTrendFunction().draw(0.0, 10)
>>> graph.add(fTrend.draw(0.0, 10))
>>> graph.add(ot.Cloud(myYField.getMesh().getVertices(), myYField.getValues()))
>>> graph.setLegends(['estimated trend', 'actual trend', 'sample'])
>>> graph.setLegendPosition('upper left')
>>> graph.setTitle('Trend estimation from a field')
>>> graph.setYTitle('values')
getBasisSequenceFactory()

Accessor to functional basis.

Returns:
myBasisSequenceFactoryBasisSequenceFactory

The functional basis \cB.

getClassName()

Accessor to the object’s name.

Returns:
class_namestr

The object class name (object.__class__.__name__).

getFittingAlgorithm()

Accessor to fitting algorithm basis.

Returns:
myFittingAlgorithmFittingAlgorithm

The fitting algorithm that estimates the empirical error on each sub-basis.

getName()

Accessor to the object’s name.

Returns:
namestr

The name of the object.

hasName()

Test if the object is named.

Returns:
hasNamebool

True if the name is not empty.

setBasisSequenceFactory(basisSequenceFactory)

Accessor to functional basis.

Parameters:
myBasisSequenceFactoryBasisSequenceFactory

The functional basis \cB.

setFittingAlgorithm(fittingAlgorithm)

Accessor to fitting algorithm basis.

Parameters:
myFittingAlgorithmFittingAlgorithm

The fitting algorithm that estimates the empirical error on each sub-basis.

setName(name)

Accessor to the object’s name.

Parameters:
namestr

The name of the object.

Examples using the class

Trend computation

Trend computation