GeneralLinearModelResult¶

class GeneralLinearModelResult(*args)¶

General linear model result.

Parameters:

inputSample, outputSampleSample: The samples $(\vect{x}_k)_{1 \leq k \leq N} \in \Rset^d$ and $(\vect{y}_k)_{1 \leq k \leq N}\in \Rset^p$ .
metaModelFunction: The meta model: $\tilde{\cM}: \Rset^d \rightarrow \Rset^p$ , defined in :eq:metaModel.
residualsPoint: The residual errors.
relativeErrorsPoint: The relative errors.
basisBasis: Functional basis of size $b$ : $(\varphi^l: \Rset^d \rightarrow \Rset^p)$ for each $l \in [1, b]$ . Its size should be equal to zero if the trend is not estimated.
trendCoefsequence of float: The trend coefficients vectors $(\vect{\alpha}^1, \dots, \vect{\alpha}^p)$ stored as a Point.
covarianceModelCovarianceModel: Covariance function of the Gaussian process with its optimized parameters.
optimalLogLikelihoodfloat: The maximum log-likelihood corresponding to the model.

Methods

`getBasis`()	Accessor to the functional basis.
`getClassName`()	Accessor to the object's name.
`getCovarianceModel`()	Accessor to the covariance model.
`getInputSample`()	Accessor to the input sample.
`getMetaModel`()	Accessor to the metamodel.
`getName`()	Accessor to the object's name.
`getNoise`()	Accessor to the Gaussian process.
`getOptimalLogLikelihood`()	Accessor to the optimal log-likelihood of the model.
`getOutputSample`()	Accessor to the output sample.
`getRelativeErrors`()	Accessor to the relative errors.
`getResiduals`()	Accessor to the residuals.
`getTrendCoefficients`()	Accessor to the trend coefficients.
`hasName`()	Test if the object is named.
`setInputSample`(sampleX)	Accessor to the input sample.
`setMetaModel`(metaModel)	Accessor to the metamodel.
`setName`(name)	Accessor to the object's name.
`setOutputSample`(sampleY)	Accessor to the output sample.
`setRelativeErrors`(relativeErrors)	Accessor to the relative errors.
`setResiduals`(residuals)	Accessor to the residuals.

Notes

The structure is usually created by the method run() of a GeneralLinearModelAlgorithm, and obtained thanks to the getResult() method.

The meta model $\tilde{\cM}: \Rset^d \rightarrow \Rset^p$ is defined by:

(1)¶ $\tilde{\cM}(\vect{x}) = \left( \begin{array}{l} \mu_1(\vect{x}) \\ \dots \\ \mu_p(\vect{x}) \end{array} \right)$

where $\mu_l(\vect{x}) = \sum_{j=1}^{b} \alpha_j^l \varphi_j^l(\vect{x})$ and $\varphi_j^l: \Rset^d \rightarrow \Rset$ are the trend functions (the $l-th$ marginal of varphi(x)).

(2)¶ $\tilde{\cM}(\vect{x}) = \left( \begin{array}{l} \mu_1\circ T(\vect{x}) \\ \dots \\ \mu_p\circ T(\vect{x}) \end{array} \right)$

Examples

Create the model $\cM: \Rset \mapsto \Rset$ and the samples:

>>> import openturns as ot
>>> f = ot.SymbolicFunction(['x'],  ['x * sin(x)'])
>>> sampleX = [[1.0], [2.0], [3.0], [4.0], [5.0], [6.0]]
>>> sampleY = f(sampleX)

Create the algorithm:

>>> basis = ot.Basis([ot.SymbolicFunction(['x'], ['x']), ot.SymbolicFunction(['x'], ['x^2'])])
>>> covarianceModel = ot.GeneralizedExponential([2.0], 2.0)
>>> algo = ot.GeneralLinearModelAlgorithm(sampleX, sampleY, covarianceModel, basis)
>>> algo.run()

Get the result:

>>> result = algo.getResult()

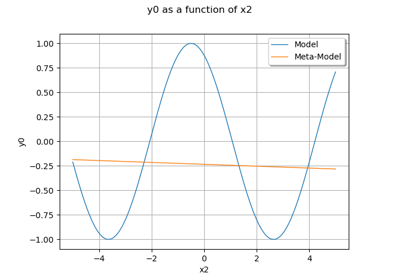
Get the meta model:

>>> metaModel = result.getMetaModel()
>>> graph = metaModel.draw(0.0, 7.0)
>>> cloud = ot.Cloud(sampleX, sampleY)
>>> cloud.setPointStyle('fcircle')
>>> graph = ot.Graph()
>>> graph.add(cloud)
>>> graph.add(f.draw(0.0, 7.0))

__init__(*args)¶

getBasis()¶

Accessor to the functional basis.

Returns:

basisBasis: Functional basis of size $b$ : $(\varphi^l: \Rset^d \rightarrow \Rset^p)$ for each $l \in [1, b]$ .

Notes

If the trend is not estimated, the collection is empty.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getCovarianceModel()¶

Accessor to the covariance model.

Returns:

covModelCovarianceModel: The covariance model of the Gaussian process W.

getInputSample()¶

Accessor to the input sample.

Returns:

inputSampleSample: The input sample.

getMetaModel()¶

Accessor to the metamodel.

Returns:

metaModelFunction: Metamodel.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getNoise()¶

Accessor to the Gaussian process.

Returns:

processProcess: Returns the Gaussian process $W$ with the optimized parameters.

getOptimalLogLikelihood()¶

Accessor to the optimal log-likelihood of the model.

Returns:

optimalLogLikelihoodfloat: The value of the log-likelihood corresponding to the model.

getOutputSample()¶

Accessor to the output sample.

Returns:

outputSampleSample: The output sample.

getRelativeErrors()¶

Accessor to the relative errors.

Returns:

relativeErrorsPoint: The relative errors defined as follows for each output of the model: $\displaystyle \frac{\sum_{i=1}^N (y_i - \hat{y_i})^2}{N \Var{\vect{Y}}}$ with $\vect{Y}$ the vector of the $N$ model’s values $y_i$ and $\hat{y_i}$ the metamodel’s values.

getResiduals()¶

Accessor to the residuals.

Returns:

residualsPoint: The residual values defined as follows for each output of the model: $\displaystyle \frac{\sqrt{\sum_{i=1}^N (y_i - \hat{y_i})^2}}{N}$ with $y_i$ the $N$ model’s values and $\hat{y_i}$ the metamodel’s values.

getTrendCoefficients()¶

Accessor to the trend coefficients.

Returns:

trendCoefPoint: The trend coefficients vectors $(\vect{\alpha}^1, \dots, \vect{\alpha}^p)$ stored as a Point.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

setInputSample(sampleX)¶

Accessor to the input sample.

Parameters:

inputSampleSample: The input sample.

setMetaModel(metaModel)¶

Accessor to the metamodel.

Parameters:

metaModelFunction: Metamodel.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

setOutputSample(sampleY)¶

Accessor to the output sample.

Parameters:

outputSampleSample: The output sample.

setRelativeErrors(relativeErrors)¶

Accessor to the relative errors.

Parameters:

relativeErrorssequence of float: The relative errors defined as follows for each output of the model: $\displaystyle \frac{\sum_{i=1}^N (y_i - \hat{y_i})^2}{N \Var{\vect{Y}}}$ with $\vect{Y}$ the vector of the $N$ model’s values $y_i$ and $\hat{y_i}$ the metamodel’s values.

setResiduals(residuals)¶

Accessor to the residuals.

Parameters:

residualssequence of float: The residual values defined as follows for each output of the model: $\displaystyle \frac{\sqrt{\sum_{i=1}^N (y_i - \hat{y_i})^2}}{N}$ with $y_i$ the $N$ model’s values and $\hat{y_i}$ the metamodel’s values.

Examples using the class¶

Create a general linear model metamodel

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page

GeneralLinearModelResult¶

Examples using the class¶