LinearLeastSquares

class LinearLeastSquares(*args)

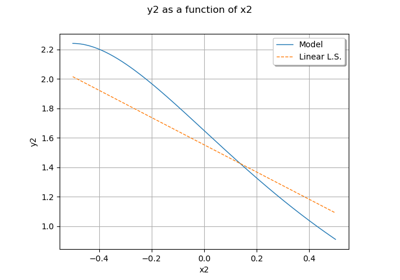
First order polynomial response surface by least squares.

Parameters:
dataIn2-d sequence of float

Input data.

dataOut2-d sequence of float

Output data. If not specified, this sample is computed such as: dataOut = h(dataIn).

Methods

getClassName()

Accessor to the object's name.

getConstant()

Get the constant vector of the approximation.

getDataIn()

Get the input data.

getDataOut()

Get the output data.

getLinear()

Get the linear matrix of the approximation.

getMetaModel()

Get an approximation of the function.

getName()

Accessor to the object's name.

hasName()

Test if the object is named.

run()

Perform the least squares approximation.

setDataOut(dataOut)

Set the output data.

setName(name)

Accessor to the object's name.

See also

QuadraticLeastSquares, LinearTaylor, QuadraticTaylor

Notes

Instead of replacing the model response h(\vect{x}) for a local approximation around a given set \vect{x}_0 of input parameters as in Taylor approximations, one may seek a global approximation of h(\vect{x}) over its whole domain of definition. A common choice to this end is global polynomial approximation.

We consider here a global approximation of the model response using a linear function:

\vect{y} \, \approx \, \widehat{h}(\vect{x}) \, = \, \sum_{j=0}^{n_X} \; a_j \; \psi_j(\vect{x})

where (a_j \, , \, j=0, \cdots,n_X) is a set of unknown coefficients and the family (\psi_j,j=0,\cdots, n_X) gathers the constant monomial 1 and the monomials of degree one x_i. Using the vector notation \vect{a} \, = \, (a_{0} , \cdots , a_{n_X} )^{\textsf{T}} and \vect{\psi}(\vect{x}) \, = \, (\psi_0(\vect{x}), \cdots, \psi_{n_X}(\vect{x}) )^{\textsf{T}}, this rewrites:

\vect{y} \, \approx \, \widehat{h}(\vect{x}) \, = \, \vect{a}^{\textsf{T}} \; \vect{\psi}(\vect{x})

A global approximation of the model response over its whole definition domain is sought. To this end, the coefficients a_j may be computed using a least squares regression approach. In this context, an experimental design \vect{\cX} =(x^{(1)},\cdots,x^{(N)}), i.e. a set of realizations of input parameters is required, as well as the corresponding model evaluations \vect{\cY} =(y^{(1)},\cdots,y^{(N)}).

The following minimization problem has to be solved:

\mbox{Find} \quad \widehat{\vect{a}} \quad \mbox{that minimizes} \quad \cJ(\vect{a}) \, = \, \sum_{i=1}^N \; \left( y^{(i)} \; - \; \vect{a}^{\textsf{T}} \vect{\psi}(\vect{x}^{(i)}) \right)^2

The solution is given by:

\widehat{\vect{a}} \, = \, \left( \vect{\vect{\Psi}}^{\textsf{T}} \vect{\vect{\Psi}} \right)^{-1} \; \vect{\vect{\Psi}}^{\textsf{T}} \; \vect{\cY}

where:

\vect{\vect{\Psi}} \, = \, (\psi_{j}(\vect{x}^{(i)}) \; , \; i=1,\cdots,N \; , \; j = 0,\cdots,n_X)

Examples

>>> import openturns as ot
>>> formulas = ['cos(x1 + x2)', '(x2 + 1) * exp(x1 - 2 * x2)']
>>> f = ot.SymbolicFunction(['x1', 'x2'], formulas)
>>> X  = [[0.5,0.5], [-0.5,-0.5], [-0.5,0.5], [0.5,-0.5]]
>>> X += [[0.25,0.25], [-0.25,-0.25], [-0.25,0.25], [0.25,-0.25]]
>>> Y = f(X)
>>> myLeastSquares = ot.LinearLeastSquares(X, Y)
>>> myLeastSquares.run()
>>> mm = myLeastSquares.getMetaModel()
>>> x = [0.1, 0.1]
>>> y = mm(x)
__init__(*args)
getClassName()

Accessor to the object’s name.

Returns:
class_namestr

The object class name (object.__class__.__name__).

getConstant()

Get the constant vector of the approximation.

Returns:
constantVectorPoint

Constant vector of the approximation, equal to a_0.

getDataIn()

Get the input data.

Returns:
dataInSample

Input data.

getDataOut()

Get the output data.

Returns:
dataOutSample

Output data. If not specified in the constructor, the sample is computed such as: dataOut = h(dataIn).

getLinear()

Get the linear matrix of the approximation.

Returns:
linearMatrixMatrix

Linear matrix of the approximation of the function h.

getMetaModel()

Get an approximation of the function.

Returns:
approximationFunction

An approximation of the function h by Linear Least Squares.

getName()

Accessor to the object’s name.

Returns:
namestr

The name of the object.

hasName()

Test if the object is named.

Returns:
hasNamebool

True if the name is not empty.

run()

Perform the least squares approximation.

setDataOut(dataOut)

Set the output data.

Parameters:
dataOut2-d sequence of float

Output data.

setName(name)

Accessor to the object’s name.

Parameters:
namestr

The name of the object.

Examples using the class

Create a linear least squares model

Create a linear least squares model

Over-fitting and model selection

Over-fitting and model selection

Use the Smolyak quadrature

Use the Smolyak quadrature

Calibration without observed inputs

Calibration without observed inputs