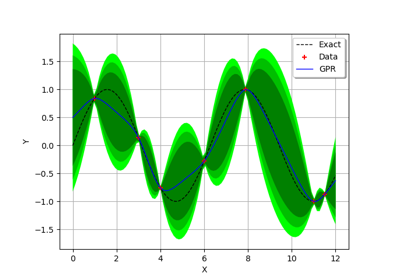
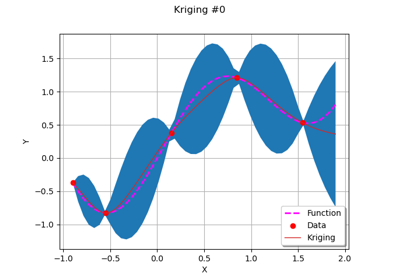
GaussianProcessRegression¶
(Source code, png)
- class GaussianProcessRegression(*args)¶
Gaussian process regression algorithm.
Warning
This class is experimental and likely to be modified in future releases. To use it, import the
openturns.experimentalsubmodule.Refer to Kriging.
- Available constructors:
GaussianProcessRegression(gprFitterResult)
GaussianProcessRegression(inputSample, outputSample, covarianceModel, trendFunction)
- Parameters:
- gprFitterResult
GaussianProcessFitterResult Result class
- inputSample, outputSample2-d sequence of float
The samples
and
upon which the meta-model is built.
- covarianceModel
CovarianceModel - covarianceModel
CovarianceModel Covariance model used for the underlying Gaussian process assumption.
- trendFunction
Function A trend function
- gprFitterResult
Methods
BuildDistribution(inputSample)Recover the distribution, with metamodel performance in mind.
Accessor to the object's name.
Accessor to the joint probability density function of the physical input vector.
Accessor to the input sample.
getName()Accessor to the object's name.
Accessor to the output sample.
Get the results of the metamodel computation.
Return the weights of the input sample.
hasName()Test if the object is named.
run()Compute the response surface.
setDistribution(distribution)Accessor to the joint probability density function of the physical input vector.
setName(name)Accessor to the object's name.
Notes
We suppose we have a sample
where
for all k, with
the model. The class allows making a gaussian process interpolating on the input samples.
Within the first constructor, we suppose all gaussian process parameters (the trend coefficients
, the scale
and the amplitude
) already calibrated and the objective is to condionning this process (the gaussian process to become interpolating over the dataset)
Within the second constructor, we assume covariance model already calibrated. A gaussian process is fitted using
GaussianProcessFitterand the sampleis considered as the trace of a this gaussian process
on
.
The Gaussian process
is defined by:
(1)¶
where:
with
and
the trend functions.
is a Gaussian process of dimension p with zero mean and covariance function
(see
CovarianceModelfor the notations).The Gaussian Process Regression meta model
is defined by:
where
is the condition
for each
.
(1) writes:
where
is a matrix in
and
.
Examples
Create the model
and the samples:
>>> import openturns as ot >>> import openturns.experimental as otexp >>> g = ot.SymbolicFunction(['x'], ['x * sin(x)']) >>> sampleX = [[1.0], [2.0], [3.0], [4.0], [5.0], [6.0], [7.0], [8.0]] >>> sampleY = g(sampleX)
Create the algorithm:
>>> basis = ot.Basis([ot.SymbolicFunction(['x'], ['x']), ot.SymbolicFunction(['x'], ['x^2'])]) >>> covarianceModel = ot.SquaredExponential([1.0]) >>> covarianceModel.setActiveParameter([]) >>> fit_algo = otexp.GaussianProcessFitter(sampleX, sampleY, covarianceModel, basis) >>> fit_algo.run()
Get the resulting meta model:
>>> fit_result = fit_algo.getResult() >>> algo = otexp.GaussianProcessRegression(fit_result) >>> algo.run() >>> result = algo.getResult() >>> metamodel = result.getMetaModel()
- __init__(*args)¶
- static BuildDistribution(inputSample)¶
Recover the distribution, with metamodel performance in mind.
For each marginal, find the best 1-d continuous parametric model else fallback to the use of a nonparametric one.
The selection is done as follow:
We start with a list of all parametric models (all factories)
For each model, we estimate its parameters if feasible.
We check then if model is valid, ie if its Kolmogorov score exceeds a threshold fixed in the MetaModelAlgorithm-PValueThreshold ResourceMap key. Default value is 5%
We sort all valid models and return the one with the optimal criterion.
For the last step, the criterion might be BIC, AIC or AICC. The specification of the criterion is done through the MetaModelAlgorithm-ModelSelectionCriterion ResourceMap key. Default value is fixed to BIC. Note that if there is no valid candidate, we estimate a non-parametric model (
KernelSmoothingorHistogram). The MetaModelAlgorithm-NonParametricModel ResourceMap key allows selecting the preferred one. Default value is HistogramOne each marginal is estimated, we use the Spearman independence test on each component pair to decide whether an independent copula. In case of non independence, we rely on a
NormalCopula.- Parameters:
- sample
Sample Input sample.
- sample
- Returns:
- distribution
Distribution Input distribution.
- distribution
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getDistribution()¶
Accessor to the joint probability density function of the physical input vector.
- Returns:
- distribution
Distribution Joint probability density function of the physical input vector.
- distribution
- getInputSample()¶
Accessor to the input sample.
- Returns:
- inputSample
Sample Input sample of a model evaluated apart.
- inputSample
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getOutputSample()¶
Accessor to the output sample.
- Returns:
- outputSample
Sample Output sample of a model evaluated apart.
- outputSample
- getResult()¶
Get the results of the metamodel computation.
- Returns:
- result
GaussianProcessRegressionResult Structure containing all the results obtained after computation and created by the method
run().
- result
- getWeights()¶
Return the weights of the input sample.
- Returns:
- weightssequence of float
The weights of the points in the input sample.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- run()¶
Compute the response surface.
Notes
It computes the kriging response surface and creates a
GaussianProcessRegressionResultstructure containing all the results.
- setDistribution(distribution)¶
Accessor to the joint probability density function of the physical input vector.
- Parameters:
- distribution
Distribution Joint probability density function of the physical input vector.
- distribution
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
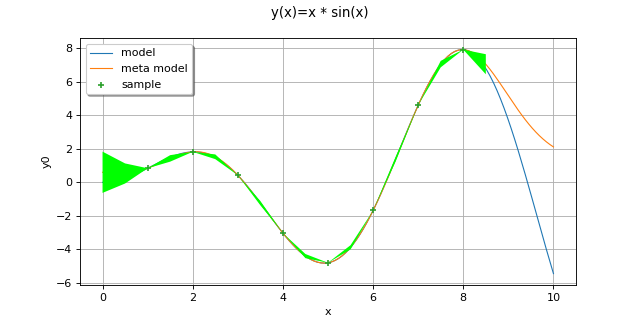
Gaussian Process Regression : cantilever beam model
 OpenTURNS
OpenTURNS