Perturbation Law Indices¶
It is required to first build a POD object based on the Kriging metamodel or on the polynomial chaos in order to compute the PLI. It also can be used only if the input parameters dimension is greater than 2 (without counting the defect).
[1]:
# import relevant module
import openturns as ot
import otpod
import numpy as np
# enable display figure in notebook
try:
%matplotlib inline
except:
pass
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/sklearn/ensemble/weight_boosting.py:29: DeprecationWarning: numpy.core.umath_tests is an internal NumPy module and should not be imported. It will be removed in a future NumPy release.
from numpy.core.umath_tests import inner1d
Generate data¶
[2]:
inputSample = ot.Sample(
[[4.59626812e+00, 7.46143339e-02, 1.02231538e+00, 8.60042277e+01],
[4.14315790e+00, 4.20801346e-02, 1.05874908e+00, 2.65757364e+01],
[4.76735111e+00, 3.72414824e-02, 1.05730385e+00, 5.76058433e+01],
[4.82811977e+00, 2.49997658e-02, 1.06954641e+00, 2.54461380e+01],
[4.48961094e+00, 3.74562922e-02, 1.04943946e+00, 6.19483646e+00],
[5.05605334e+00, 4.87599783e-02, 1.06520409e+00, 3.39024904e+00],
[5.69679328e+00, 7.74915877e-02, 1.04099514e+00, 6.50990466e+01],
[5.10193991e+00, 4.35520544e-02, 1.02502536e+00, 5.51492592e+01],
[4.04791970e+00, 2.38565932e-02, 1.01906882e+00, 2.07875350e+01],
[4.66238956e+00, 5.49901237e-02, 1.02427200e+00, 1.45661275e+01],
[4.86634219e+00, 6.04693570e-02, 1.08199374e+00, 1.05104730e+00],
[4.13519347e+00, 4.45225831e-02, 1.01900124e+00, 5.10117047e+01],
[4.92541940e+00, 7.87692335e-02, 9.91868726e-01, 8.32302238e+01],
[4.70722074e+00, 6.51799251e-02, 1.10608515e+00, 3.30181002e+01],
[4.29040932e+00, 1.75426222e-02, 9.75678838e-01, 2.28186756e+01],
[4.89291400e+00, 2.34997929e-02, 1.07669835e+00, 5.38926138e+01],
[4.44653744e+00, 7.63175936e-02, 1.06979154e+00, 5.19109415e+01],
[3.99977452e+00, 5.80430585e-02, 1.01850716e+00, 7.61988190e+01],
[3.95491570e+00, 1.09302814e-02, 1.03687664e+00, 6.09981789e+01],
[5.16424368e+00, 2.69026464e-02, 1.06673711e+00, 2.88708887e+01],
[5.30491620e+00, 4.53802273e-02, 1.06254792e+00, 3.03856837e+01],
[4.92809155e+00, 1.20616369e-02, 1.00700410e+00, 7.02512744e+00],
[4.68373805e+00, 6.26028935e-02, 1.05152117e+00, 4.81271603e+01],
[5.32381954e+00, 4.33013582e-02, 9.90522007e-01, 6.56015973e+01],
[4.35455857e+00, 1.23814619e-02, 1.01810539e+00, 1.10769534e+01]])
signals = ot.Sample(
[[ 37.305445], [ 35.466919], [ 43.187991], [ 45.305165], [ 40.121222], [ 44.609524],
[ 45.14552 ], [ 44.80595 ], [ 35.414039], [ 39.851778], [ 42.046049], [ 34.73469 ],
[ 39.339349], [ 40.384559], [ 38.718623], [ 46.189709], [ 36.155737], [ 31.768369],
[ 35.384313], [ 47.914584], [ 46.758537], [ 46.564428], [ 39.698493], [ 45.636588],
[ 40.643948]])
[3]:
# signal detection threshold
detection = 38.
Build POD with Kriging model¶
Running the Kriging based POD¶
[4]:
krigingPOD = otpod.KrigingPOD(inputSample, signals, detection)
# we can change all simulation size parameters as we are not interested in having an accurate POD curve
krigingPOD.setSamplingSize(200)
krigingPOD.setSimulationSize(50)
krigingPOD.run()
Start optimizing covariance model parameters...
Kriging optimizer completed
kriging validation Q2 (>0.9): 1.0000
Computing POD per defect: [==================================================] 100.00% Done
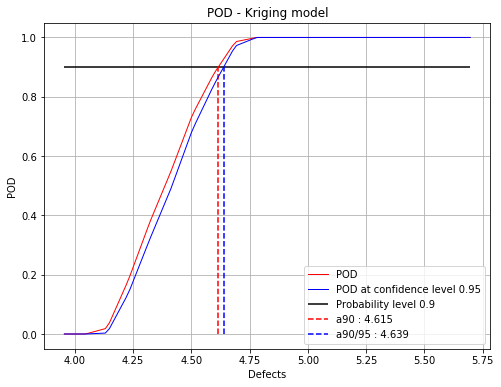
Show POD graphs¶
[5]:
fig, ax = krigingPOD.drawPOD(probabilityLevel=0.9, confidenceLevel=0.95,
name='figure/PODKriging.png')
# The figure is saved in PODPolyChaos.png
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
Build POD with polynomial chaos model¶
Running the chaos based POD¶
[6]:
chaosPOD = otpod.PolynomialChaosPOD(inputSample, signals, detection)
# we can change all simulation size parameters as we are not interested in having an accurate POD curve
chaosPOD.setSamplingSize(200)
chaosPOD.setSimulationSize(50)
chaosPOD.run()
Start build polynomial chaos model...
Polynomial chaos model completed
Polynomial chaos validation R2 (>0.8) : 0.9999
Polynomial chaos validation Q2 (>0.8) : 0.9987
Computing POD per defect: [==================================================] 100.00% Done
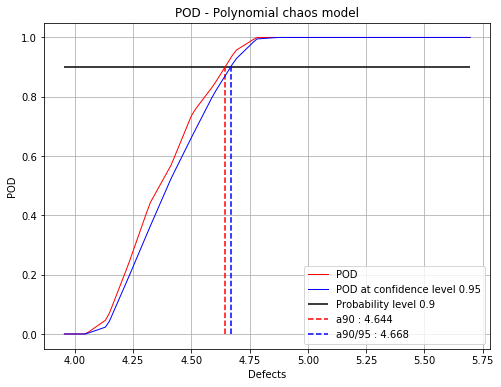
Show POD graphs¶
[7]:
fig, ax = chaosPOD.drawPOD(probabilityLevel=0.9, confidenceLevel=0.95,
name='figure/PODChaos.png')
# The figure is saved in PODPolyChaos.png
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
Run the sensitivity analysis¶
The sensitivity analysis can only be performed with POD computed with a kriging metamodel or a polynomial chaos.
The PLI are computed for the defect sizes defined in the POD study. However, if the probability estimate for a defect size is less than 1e-3 or greater than 0.999, then the indices are not computed.
The PLI can be computed either with perturbed mean or a perturbed variance. Two dedicated classes exists for each case.
Mean perturbation¶
For the mean perturbation, it is possible to change the type of the mean shifting. If sigmaScaled = False, the given delta values are the new marginal means. If sigmaScaled = True, then \(newMean = mean + sigma \times delta\), where sigma is the standard deviation of each marginals.
It is adviced to set the sigmaScaled parameter to True when the input distribution are not equal.
with a Kriging POD¶
[8]:
# the delta values
deltas = np.linspace(-1, 1, 6)
# sigma scaled is activated because the input distributions are not the same
pliMean = otpod.PLIMean(krigingPOD, deltas, sigmaScaled=True)
pliMean.run()
WARNING:root:The indices were estimated only for the following defect: 4.14, 4.23, 4.32, 4.41, 4.50, 4.60, 4.69, because the probability estimate is too small or too big for other defect values.
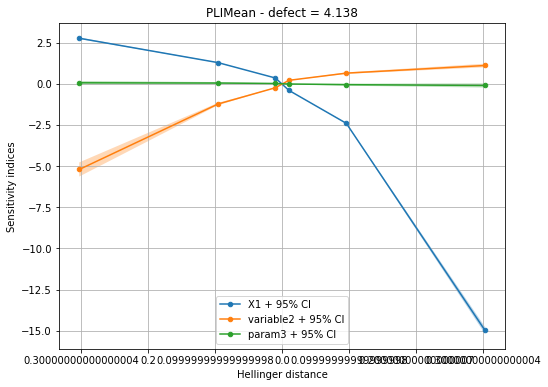
Draw the figure with given labels¶
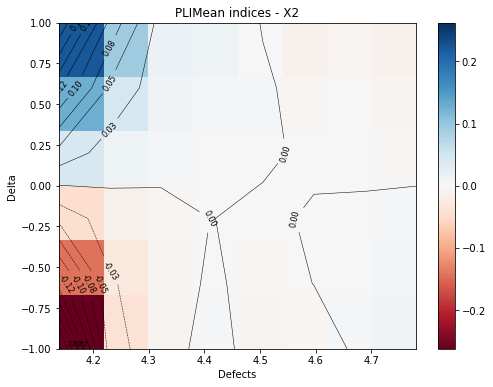
The indices can be displayed either for a specific defect size. In this case, indices for all margins are plotted in the same figure. You can choose to display the indices with respect to the Hellinger distance (default case) in order to compare in the same scale the indices.
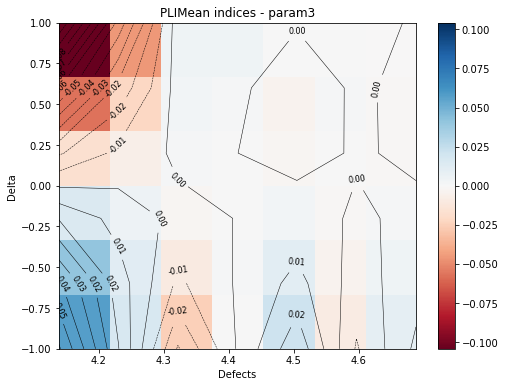
The second graph is a 2d contour plot where the indices for a given margin are plotted with respect to the defect size and the delta values. It enables you to compare the indices depending of the defect size.
[9]:
label = ['X1', 'variable2', 'param3']
[10]:
idefect = 2
fig, ax = pliMean.drawIndices(idefect, confidenceLevel=0.95,
label=label, hellinger=True)
ax.legend(loc='lower center')
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
[11]:
marginal = 2
fig, ax = pliMean.drawContourIndices(marginal, label[marginal])
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
Get the numerical results¶
The PLI values can be obtained thanks to the method getIndices. You can to get:
all indices values
indices for a specific marginal
indices for a specific delta value
indices for a specific defect size
a combination of above values
The nan values corresponds to the defect sizes for which the indices cannot be computed because the probability estimate is too small or too large.
[12]:
print('Indices for marginal 1: ')
print(pliMean.getIndices(marginal=1))
Indices for marginal 1:
[[ nan nan -5.20484953 -0.46784362 -0.23294571 -0.14515493
-0.1235924 -0.08908541 -0.05218406 nan nan nan
nan nan nan nan nan nan
nan nan]
[ nan nan -1.23231505 -0.23064471 -0.12821335 -0.08116785
-0.06974791 -0.05172207 -0.02538093 nan nan nan
nan nan nan nan nan nan
nan nan]
[ nan nan -0.24367882 -0.06513973 -0.03950675 -0.02547104
-0.02179865 -0.01680401 -0.00708865 nan nan nan
nan nan nan nan nan nan
nan nan]
[ nan nan 0.20573065 0.05971306 0.03811938 0.02472888
0.02087097 0.01672381 0.00604371 nan nan nan
nan nan nan nan nan nan
nan nan]
[ nan nan 0.64276482 0.17388364 0.11452088 0.07408223
0.06100422 0.05098839 0.01555555 nan nan nan
nan nan nan nan nan nan
nan nan]
[ nan nan 1.10647782 0.27723651 0.18990485 0.12399895
0.09843456 0.08696171 0.0226057 nan nan nan
nan nan nan nan nan nan
nan nan]]
[13]:
print('Indices for defect 4: ')
print(pliMean.getIndices(idefect=4))
Indices for defect 4:
[[ 1.10336807e+00 -2.32945706e-01 -2.48287972e-02]
[ 6.51182636e-01 -1.28213346e-01 -9.51075386e-03]
[ 2.09833716e-01 -3.95067466e-02 -2.13429231e-03]
[-2.50473569e-01 3.81193815e-02 1.45062730e-03]
[-1.29172764e+00 1.14520879e-01 3.04535446e-03]
[-5.73347022e+00 1.89904848e-01 4.63723691e-03]]
PLI object for a specific defect size¶
From the base PLI object computed for each defect size, you can have access to more results :
the confidence interval
the perturbed probability estimate
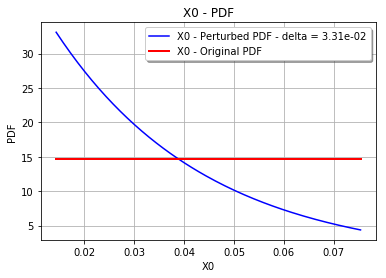
draw the perturbed marginal density
[14]:
# get PLI object for the 3rd defect
pliMeanDefect3 = pliMean.getPLIObject(3)
print("Perturbed probability estimate : ")
print(pliMeanDefect3.getPerturbedProbabilityEstimate())
fig, ax = pliMeanDefect3.drawMarginal1DPDF(marginal=0, idelta=1)
fig.show()
Perturbed probability estimate :
[[0.58159571 0.13891125 0.20724209]
[0.4005364 0.16568551 0.20637717]
[0.26164943 0.19143028 0.20490247]
[0.15302838 0.21607549 0.20270131]
[0.07134159 0.23935487 0.19959424]
[0.01858485 0.26042852 0.19508161]]
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
with polynomial chaos¶
[15]:
# the delta values
deltas = np.linspace(-1, 1, 6)
# sigma scaled is activated because the input distributions are not the same
pliMean = otpod.PLIMean(chaosPOD, deltas, sigmaScaled=True)
pliMean.run()
WARNING:root:The indices were estimated only for the following defect: 4.14, 4.23, 4.32, 4.41, 4.50, 4.60, 4.69, 4.78, because the probability estimate is too small or too big for other defect values.
[16]:
marginal = 2
fig, ax = pliMean.drawContourIndices(marginal)
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
Variance perturbation¶
For the variance perturbation, the delta values must be greater than 0. The delta values corresponds to:
the new variance if coefScaled = False
\(newCov = delta + cov\) if covScaled = True, this increases the coefficient of variation by delta. The new variance is computed such that the mean does not change.
It is also possible to define the delta values independently for each margin.
[17]:
# the delta values
deltas = np.linspace(-0.02, 0.02, 3)
# with coef scaled
pliVar = otpod.PLIVariance(krigingPOD, deltas, covScaled=True)
pliVar.run()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/otpod-0.3-py3.6.egg/otpod/_pli.py:689: RuntimeWarning: overflow encountered in exp
WARNING:root:The indices were estimated only for the following defect: 4.14, 4.23, 4.32, 4.41, 4.50, 4.60, 4.69, because the probability estimate is too small or too big for other defect values.
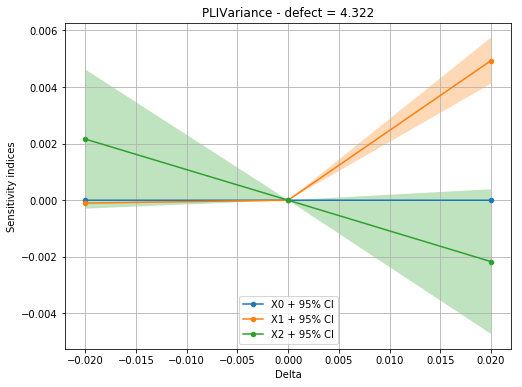
With the Hellinger distance, we can see that the perturbed variance is not equivalent for all margins.
[18]:
idefect = 4
fig, ax = pliVar.drawIndices(idefect, confidenceLevel=0.95,
hellinger=False)
ax.legend(loc='lower center')
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
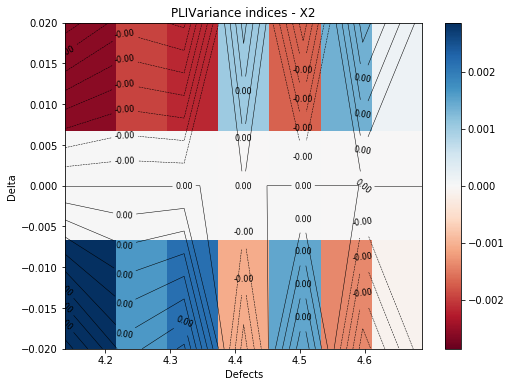
[19]:
marginal = 2
fig, ax = pliVar.drawContourIndices(marginal)
fig.show()
/calcul/home/dumas/anaconda/lib/python3.6/site-packages/matplotlib/figure.py:459: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
[ ]:
 otpod
otpod