Calibration of the deflection of a tube¶

Description¶

We consider the deflection of a tube under a vertical stress.

The parameters of the model are:

F : the strength,
L : the length of the tube,
a : position of the force,
D : external diameter of the tube,
d : internal diameter of the tube,
E : Young modulus.

The following figure presents the internal and external diameter of the tube:

The area moment of inertia of the cross section about the neutral axis of a round tube (i.e. perpendicular to the section) with external and internal diameters $D$ and $d$ are:

$I = \frac{\pi (D^4-d^4)}{32}.$

The vertical deflection at point $x=a$ is:

$g_1(X) = - F \frac{a^2 (L-a)^2}{3 E L I},$

where $X=(F,L,a,D,d,E)$ . The angle of the tube at the left end is:

$g_2(X) = - F \frac{b (L^2-b^2)}{6 E L I},$

and the angle of the tube at the right end is:

$g_3(X) = F \frac{a (L^2-a^2)}{6 E L I}.$

The following table presents the distributions of the random variables. These variables are assumed to be independent.

Variable	Distribution
F	Normal(1,0.1)
L	Normal(1.5,0.01)
a	Uniform(0.7,1.2)
D	Triangular(0.75,0.8,0.85)
d	Triangular(0.09,0.1,0.11)
E	Normal(200000,2000)

References¶

Deflection of beams by Russ Elliott. http://www.clag.org.uk/beam.html
https://upload.wikimedia.org/wikipedia/commons/f/ff/Simple_beam_with_offset_load.svg
https://en.wikipedia.org/wiki/Deflection_(engineering)
https://mechanicalc.com/reference/beam-deflection-tables
https://en.wikipedia.org/wiki/Second_moment_of_area
Shigley’s Mechanical Engineering Design (9th Edition), Richard G. Budynas, J. Keith Nisbettn, McGraw Hill (2011)
Mechanics of Materials (7th Edition), James M. Gere, Barry J. Goodno, Cengage Learning (2009)
Statics and Mechanics of Materials (5th Edition), Ferdinand Beer, E. Russell Johnston, Jr., John DeWolf, David Mazurek. Mc Graw Hill (2011) Chapter 15: deflection of beams.

Create a calibration problem¶

[1]:

import openturns as ot

We use the variable names De for the external diameter and di for the internal diameter because the symbolic function engine is not case sensitive, hence the variable names D and d would not be distiguished.

[2]:

inputsvars=["F","L","a","De","di","E"]
formula = "var I:=pi_*(De^4-di^4)/32; var b:=L-a; g1:=-F*a^2*(L-a)^2/(3*E*L*I); g2:=-F*b*(L^2-b^2)/(6*E*L*I); g3:=F*a*(L^2-a^2)/(6*E*L*I)"
g = ot.SymbolicFunction(inputsvars,["g1","g2","g3"],formula)
g.setOutputDescription(["Deflection","Left angle","Right angle"])

[3]:

XF=ot.Normal(1,0.1)
XE=ot.Normal(200000,2000)
XF.setDescription(["Force"])
XE.setDescription(["Young Modulus"])

[4]:

XL = ot.Dirac(1.5)
Xa = ot.Dirac(1.0)
XD = ot.Dirac(0.8)
Xd = ot.Dirac(0.1)
XL.setDescription(["Longueur"])
Xa.setDescription(["Location"])
XD.setDescription(["External diameter"])
Xd.setDescription(["Internal diameter"])

[5]:

inputDistribution = ot.ComposedDistribution([XF,XL,Xa,XD,Xd,XE])

[6]:

sampleSize = 100
inputSample = inputDistribution.getSample(sampleSize)
inputSample[0:5]

[6]:

	Force	Longueur	Location	External diameter	Internal diameter	Young Modulus
0	1.0608201651218765	1.5	1.0	0.8	0.1	196966.07036307675
1	0.8733826897783343	1.5	1.0	0.8	0.1	197401.2408213367
2	0.9561734380039586	1.5	1.0	0.8	0.1	200460.74487807832
3	1.1205478200828576	1.5	1.0	0.8	0.1	193805.25155946863
4	0.7818614765383486	1.5	1.0	0.8	0.1	200026.45999395067

[7]:

outputDeflection = g(inputSample)
outputDeflection[0:5]

[7]:

	Deflection	Left angle	Right angle
0	-7.442589066378747e-06	-1.4885178132757494e-05	1.8606472665946867e-05
1	-6.114041697475519e-06	-1.2228083394951039e-05	1.52851042436888e-05
2	-6.591451026631792e-06	-1.3182902053263584e-05	1.647862756657948e-05
3	-7.98984857356334e-06	-1.597969714712668e-05	1.997462143390835e-05
4	-5.401520898870577e-06	-1.0803041797741154e-05	1.3503802247176442e-05

[8]:

observationNoiseSigma = [0.1e-6,0.05e-5,0.05e-5]
observationNoiseCovariance = ot.CovarianceMatrix(3)
for i in range(3):
    observationNoiseCovariance[i,i] = observationNoiseSigma[i]**2

[9]:

noiseSigma = ot.Normal([0.,0.,0.],observationNoiseCovariance)
sampleObservationNoise = noiseSigma.getSample(sampleSize)
observedOutput = outputDeflection + sampleObservationNoise
observedOutput[0:5]

[9]:

	Deflection	Left angle	Right angle
0	-7.356762209314677e-06	-1.5338461089948315e-05	1.814806773342329e-05
1	-5.997719622988609e-06	-1.2077124238651994e-05	1.553026987801388e-05
2	-6.543908569160418e-06	-1.3577254181436902e-05	1.614390297308445e-05
3	-8.003641369111095e-06	-1.646546275829769e-05	1.9380702536539273e-05
4	-5.258700570801308e-06	-1.1097656728695641e-05	1.2637714263644793e-05

[10]:

observedInput = ot.Sample(sampleSize,2)
observedInput[:,0] = inputSample[:,0] # F
observedInput[:,1] = inputSample[:,5] # E
observedInput.setDescription(["Force","Young Modulus"])
observedInput[0:5]

[10]:

	Force	Young Modulus
0	1.0608201651218765	196966.07036307675
1	0.8733826897783343	197401.2408213367
2	0.9561734380039586	200460.74487807832
3	1.1205478200828576	193805.25155946863
4	0.7818614765383486	200026.45999395067

[11]:

fullSample = ot.Sample(sampleSize,5)
fullSample[:,0:2] = observedInput
fullSample[:,2:5] = observedOutput
fullSample.setDescription(["Force","Young","Deflection","Left Angle","Right Angle"])
fullSample[0:5]

[11]:

	Force	Young	Deflection	Left Angle	Right Angle
0	1.0608201651218765	196966.07036307675	-7.356762209314677e-06	-1.5338461089948315e-05	1.814806773342329e-05
1	0.8733826897783343	197401.2408213367	-5.997719622988609e-06	-1.2077124238651994e-05	1.553026987801388e-05
2	0.9561734380039586	200460.74487807832	-6.543908569160418e-06	-1.3577254181436902e-05	1.614390297308445e-05
3	1.1205478200828576	193805.25155946863	-8.003641369111095e-06	-1.646546275829769e-05	1.9380702536539273e-05
4	0.7818614765383486	200026.45999395067	-5.258700570801308e-06	-1.1097656728695641e-05	1.2637714263644793e-05

[12]:

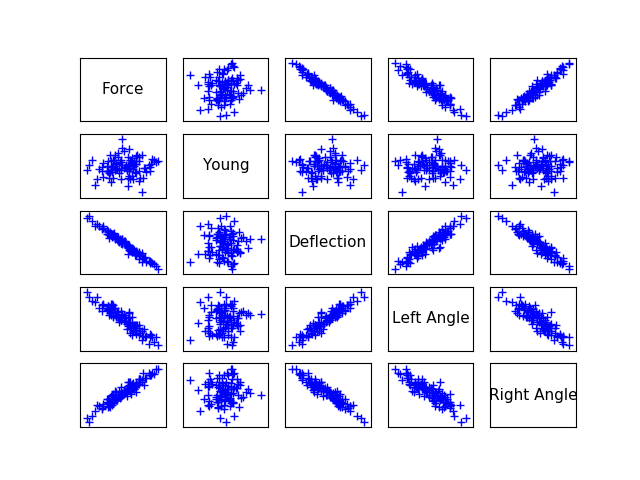
ot.Pairs(fullSample)

[12]:

../../_images/examples_calibration_calibration_deflection_tube_16_0.png

Setting up the calibration¶

[13]:

XL = 1.4 # Exact : 1.5
Xa = 1.2 # Exact : 1.0
XD = 0.7 # Exact : 0.8
Xd = 0.2 # Exact : 0.1
thetaPrior = ot.Point([XL,Xa,XD,Xd])

[14]:

sigmaXL = 0.1 * XL
sigmaXa = 0.1 * Xa
sigmaXD = 0.1 * XD
sigmaXd = 0.1 * Xd
parameterCovariance = ot.CovarianceMatrix(4)
parameterCovariance[0,0] = sigmaXL**2
parameterCovariance[1,1] = sigmaXa**2
parameterCovariance[2,2] = sigmaXD**2
parameterCovariance[3,3] = sigmaXd**2
parameterCovariance

[14]:

[[ 0.0196 0 0 0 ]
[ 0 0.0144 0 0 ]
[ 0 0 0.0049 0 ]
[ 0 0 0 0.0004 ]]

[15]:

calibratedIndices = [1,2,3,4]
calibrationFunction = ot.ParametricFunction(g, calibratedIndices, thetaPrior)

[16]:

sigmaObservation = [0.2e-6,0.03e-5,0.03e-5] # Exact : 0.1e-6

[17]:

errorCovariance = ot.CovarianceMatrix(3)
errorCovariance[0,0] = sigmaObservation[0]**2
errorCovariance[1,1] = sigmaObservation[1]**2
errorCovariance[2,2] = sigmaObservation[2]**2

[18]:

calibrationFunction.setParameter(thetaPrior)
predictedOutput = calibrationFunction(observedInput)
predictedOutput[0:5]

[18]:

	Deflection	Left angle	Right angle
0	-3.154534354474193e-06	-1.0515114514913978e-05	1.7087061086735213e-05
1	-2.591430805511134e-06	-8.638102685037113e-06	1.4036916863185308e-05
2	-2.79378029928786e-06	-9.312600997626203e-06	1.5132976621142579e-05
3	-3.3864897803118274e-06	-1.1288299267706095e-05	1.8343486310022407e-05
4	-2.2894295372118615e-06	-7.631431790706208e-06	1.2401076659897585e-05

A visualisation class¶

[19]:

"""
A graphics class to analyze the results of calibration.
"""

import pylab as pl
import openturns as ot
import openturns.viewer as otv

class CalibrationAnalysis:
    def __init__(self,calibrationResult,model,inputObservations,outputObservations):
        """
        Plots the prior and posterior distribution of the calibrated parameter theta.

        Parameters
        ----------
        calibrationResult : :class:`~openturns.calibrationResult`
            The result of a calibration.

        model : 2-d sequence of float
            The function to calibrate.

        inputObservations : :class:`~openturns.Sample`
            The sample of input values of the model linked to the observations.

        outputObservations : 2-d sequence of float
            The sample of output values of the model linked to the observations.
        """
        self.model = model
        self.outputAtPrior = None
        self.outputAtPosterior = None
        self.calibrationResult = calibrationResult
        self.observationColor = "blue"
        self.priorColor = "red"
        self.posteriorColor = "green"
        self.inputObservations = inputObservations
        self.outputObservations = outputObservations
        self.unitlength = 6 # inch
        # Compute yAtPrior
        meanPrior = calibrationResult.getParameterPrior().getMean()
        model.setParameter(meanPrior)
        self.outputAtPrior=model(inputObservations)
        # Compute yAtPosterior
        meanPosterior = calibrationResult.getParameterPosterior().getMean()
        model.setParameter(meanPosterior)
        self.outputAtPosterior=model(inputObservations)
        return None

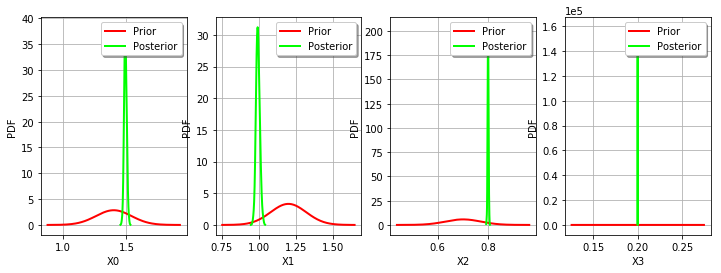
    def drawParameterDistributions(self):
        """
        Plots the prior and posterior distribution of the calibrated parameter theta.
        """
        thetaPrior = self.calibrationResult.getParameterPrior()
        thetaDescription = thetaPrior.getDescription()
        thetaPosterior = self.calibrationResult.getParameterPosterior()
        thetaDim = thetaPosterior.getDimension()
        fig = pl.figure(figsize=(12, 4))
        for i in range(thetaDim):
            graph = ot.Graph("",thetaDescription[i],"PDF",True,"topright")
            # Prior distribution
            thetaPrior_i = thetaPrior.getMarginal(i)
            priorPDF = thetaPrior_i.drawPDF()
            priorPDF.setColors([self.priorColor])
            priorPDF.setLegends(["Prior"])
            graph.add(priorPDF)
            # Posterior distribution
            thetaPosterior_i = thetaPosterior.getMarginal(i)
            postPDF = thetaPosterior_i.drawPDF()
            postPDF.setColors([self.posteriorColor])
            postPDF.setLegends(["Posterior"])
            graph.add(postPDF)
            '''
            If the prior is a Dirac, set the vertical axis bounds to the posterior.
            Otherwise, the Dirac set to [0,1], where the 1 can be much larger
            than the maximum PDF of the posterior.
            '''
            if (thetaPrior_i.getName()=="Dirac"):
                # The vertical (PDF) bounds of the posterior
                postbb = postPDF.getBoundingBox()
                pdf_upper = postbb.getUpperBound()[1]
                pdf_lower = postbb.getLowerBound()[1]
                # Set these bounds to the graph
                bb = graph.getBoundingBox()
                graph_upper = bb.getUpperBound()
                graph_upper[1] = pdf_upper
                bb.setUpperBound(graph_upper)
                graph_lower = bb.getLowerBound()
                graph_lower[1] = pdf_lower
                bb.setLowerBound(graph_lower)
                graph.setBoundingBox(bb)
            # Add it to the graphics
            ax = fig.add_subplot(1, thetaDim, i+1)
            _ = otv.View(graph, figure=fig, axes=[ax])
        return fig

    def drawObservationsVsPredictions(self):
        """
        Plots the output of the model depending
        on the output observations before and after calibration.
        """

        ySize = self.outputObservations.getSize()
        yDim = self.outputObservations.getDimension()
        graph = ot.Graph("","Observations","Predictions",True,"topleft")
        # Plot the diagonal
        if (yDim==1):
            graph = self._drawObservationsVsPredictions1Dimension(self.outputObservations,self.outputAtPrior,self.outputAtPosterior)
        elif (ySize==1):
            outputObservations = ot.Sample(self.outputObservations[0],1)
            outputAtPrior = ot.Sample(self.outputAtPrior[0],1)
            outputAtPosterior = ot.Sample(self.outputAtPosterior[0],1)
            graph = self._drawObservationsVsPredictions1Dimension(outputObservations,outputAtPrior,outputAtPosterior)
        else:
            fig = pl.figure(figsize=(self.unitlength*yDim, self.unitlength))
            for i in range(yDim):
                outputObservations = self.outputObservations[:,i]
                outputAtPrior = self.outputAtPrior[:,i]
                outputAtPosterior = self.outputAtPosterior[:,i]
                graph = self._drawObservationsVsPredictions1Dimension(outputObservations,outputAtPrior,outputAtPosterior)
                ax = fig.add_subplot(1, yDim, i+1)
                _ = otv.View(graph, figure=fig, axes=[ax])

        return graph

    def _drawObservationsVsPredictions1Dimension(self,outputObservations,outputAtPrior,outputAtPosterior):
        """
        Plots the output of the model depending
        on the output observations before and after calibration.
        Can manage only 1D samples.
        """
        yDim = outputObservations.getDimension()
        ydescription = outputObservations.getDescription()
        xlabel = "%s Observations" % (ydescription[0])
        ylabel = "%s Predictions" % (ydescription[0])
        graph = ot.Graph("",xlabel,ylabel,True,"topleft")
        # Plot the diagonal
        if (yDim==1):
            curve = ot.Curve(outputObservations, outputObservations)
            curve.setColor(self.observationColor)
            graph.add(curve)
        else:
            raise TypeError('Output observations are not 1D.')
        # Plot the predictions before
        yPriorDim = outputAtPrior.getDimension()
        if (yPriorDim==1):
            cloud = ot.Cloud(outputObservations, outputAtPrior)
            cloud.setColor(self.priorColor)
            cloud.setLegend("Prior")
            graph.add(cloud)
        else:
            raise TypeError('Output prior predictions are not 1D.')
        # Plot the predictions after
        yPosteriorDim = outputAtPosterior.getDimension()
        if (yPosteriorDim==1):
            cloud = ot.Cloud(outputObservations, outputAtPosterior)
            cloud.setColor(self.posteriorColor)
            cloud.setLegend("Posterior")
            graph.add(cloud)
        else:
            raise TypeError('Output posterior predictions are not 1D.')
        return graph

    def drawResiduals(self):
        """
        Plot the distribution of the residuals and
        the distribution of the observation errors.
        """
        ySize = self.outputObservations.getSize()
        yDim = self.outputObservations.getDimension()
        yPriorSize = self.outputAtPrior.getSize()
        yPriorDim = self.outputAtPrior.getDimension()
        if (yDim==1):
            observationsError = self.calibrationResult.getObservationsError()
            graph = self._drawResiduals1Dimension(self.outputObservations,self.outputAtPrior,self.outputAtPosterior,observationsError)
        elif (ySize==1):
            outputObservations = ot.Sample(self.outputObservations[0],1)
            outputAtPrior = ot.Sample(self.outputAtPrior[0],1)
            outputAtPosterior = ot.Sample(self.outputAtPosterior[0],1)
            observationsError = self.calibrationResult.getObservationsError()
            # In this case, we cannot draw observationsError ; just
            # pass the required input argument, but it is not actually used.
            graph = self._drawResiduals1Dimension(outputObservations,outputAtPrior,outputAtPosterior,observationsError)
        else:
            observationsError = self.calibrationResult.getObservationsError()
            fig = pl.figure(figsize=(self.unitlength*yDim, self.unitlength))
            for i in range(yDim):
                outputObservations = self.outputObservations[:,i]
                outputAtPrior = self.outputAtPrior[:,i]
                outputAtPosterior = self.outputAtPosterior[:,i]
                observationsErrorYi = observationsError.getMarginal(i)
                graph = self._drawResiduals1Dimension(outputObservations,outputAtPrior,outputAtPosterior,observationsErrorYi)
                ax = fig.add_subplot(1, yDim, i+1)
                _ = otv.View(graph, figure=fig, axes=[ax])
        return graph

    def _drawResiduals1Dimension(self,outputObservations,outputAtPrior,outputAtPosterior,observationsError):
        """
        Plot the distribution of the residuals and
        the distribution of the observation errors.
        Can manage only 1D samples.
        """
        ydescription = outputObservations.getDescription()
        xlabel = "%s Residuals" % (ydescription[0])
        graph = ot.Graph("Residuals analysis",xlabel,"Probability distribution function",True,"topright")
        yDim = outputObservations.getDimension()
        yPriorDim = outputAtPrior.getDimension()
        yPosteriorDim = outputAtPrior.getDimension()
        if (yDim==1) and (yPriorDim==1) :
            posteriorResiduals = outputObservations - outputAtPrior
            kernel = ot.KernelSmoothing()
            fittedDist = kernel.build(posteriorResiduals)
            residualPDF = fittedDist.drawPDF()
            residualPDF.setColors([self.priorColor])
            residualPDF.setLegends(["Prior"])
            graph.add(residualPDF)
        else:
            raise TypeError('Output prior observations are not 1D.')
        if (yDim==1) and (yPosteriorDim==1) :
            posteriorResiduals = outputObservations - outputAtPosterior
            kernel = ot.KernelSmoothing()
            fittedDist = kernel.build(posteriorResiduals)
            residualPDF = fittedDist.drawPDF()
            residualPDF.setColors([self.posteriorColor])
            residualPDF.setLegends(["Posterior"])
            graph.add(residualPDF)
        else:
            raise TypeError('Output posterior observations are not 1D.')
        # Plot the distribution of the observation errors
        if (observationsError.getDimension()==1):
            # In the other case, we just do not plot
            obserrgraph = observationsError.drawPDF()
            obserrgraph.setColors([self.observationColor])
            obserrgraph.setLegends(["Observation errors"])
            graph.add(obserrgraph)
        return graph

    def drawObservationsVsInputs(self):
        """
        Plots the observed output of the model depending
        on the observed input before and after calibration.
        """
        xSize = self.inputObservations.getSize()
        ySize = self.outputObservations.getSize()
        xDim = self.inputObservations.getDimension()
        yDim = self.outputObservations.getDimension()
        xdescription = self.inputObservations.getDescription()
        ydescription = self.outputObservations.getDescription()
        # Observations
        if (xDim==1) and (yDim==1):
            graph = self._drawObservationsVsInputs1Dimension(self.inputObservations,self.outputObservations,self.outputAtPrior,self.outputAtPosterior)
        elif (xSize==1) and (ySize==1):
            inputObservations = ot.Sample(self.inputObservations[0],1)
            outputObservations = ot.Sample(self.outputObservations[0],1)
            outputAtPrior = ot.Sample(self.outputAtPrior[0],1)
            outputAtPosterior = ot.Sample(self.outputAtPosterior[0],1)
            graph = self._drawObservationsVsInputs1Dimension(inputObservations,outputObservations,outputAtPrior,outputAtPosterior)
        else:
            fig = pl.figure(figsize=(xDim*self.unitlength, yDim*self.unitlength))
            for i in range(xDim):
                for j in range(yDim):
                    k = xDim * j + i
                    inputObservations = self.inputObservations[:,i]
                    outputObservations = self.outputObservations[:,j]
                    outputAtPrior = self.outputAtPrior[:,j]
                    outputAtPosterior = self.outputAtPosterior[:,j]
                    graph = self._drawObservationsVsInputs1Dimension(inputObservations,outputObservations,outputAtPrior,outputAtPosterior)
                    ax = fig.add_subplot(yDim, xDim, k+1)
                    _ = otv.View(graph, figure=fig, axes=[ax])
        return graph

    def _drawObservationsVsInputs1Dimension(self,inputObservations,outputObservations,outputAtPrior,outputAtPosterior):
        """
        Plots the observed output of the model depending
        on the observed input before and after calibration.
        Can manage only 1D samples.
        """
        xDim = inputObservations.getDimension()
        if (xDim!=1):
            raise TypeError('Input observations are not 1D.')
        yDim = outputObservations.getDimension()
        xdescription = inputObservations.getDescription()
        ydescription = outputObservations.getDescription()
        graph = ot.Graph("",xdescription[0],ydescription[0],True,"topright")
        # Observations
        if (yDim==1):
            cloud = ot.Cloud(inputObservations,outputObservations)
            cloud.setColor(self.observationColor)
            cloud.setLegend("Observations")
            graph.add(cloud)
        else:
            raise TypeError('Output observations are not 1D.')
        # Model outputs before calibration
        yPriorDim = outputAtPrior.getDimension()
        if (yPriorDim==1):
            cloud = ot.Cloud(inputObservations,outputAtPrior)
            cloud.setColor(self.priorColor)
            cloud.setLegend("Prior")
            graph.add(cloud)
        else:
            raise TypeError('Output prior predictions are not 1D.')
        # Model outputs after calibration
        yPosteriorDim = outputAtPosterior.getDimension()
        if (yPosteriorDim==1):
            cloud = ot.Cloud(inputObservations,outputAtPosterior)
            cloud.setColor(self.posteriorColor)
            cloud.setLegend("Posterior")
            graph.add(cloud)
        else:
            raise TypeError('Output posterior predictions are not 1D.')
        return graph

Calibration with gaussian non linear least squares¶

[20]:

algo = ot.GaussianNonLinearCalibration(calibrationFunction, observedInput, observedOutput, thetaPrior, parameterCovariance, errorCovariance)

[21]:

algo.run()

[22]:

calibrationResult = algo.getResult()

Analysis of the results¶

[23]:

thetaMAP = calibrationResult.getParameterMAP()
thetaMAP

[23]:

[1.49042,0.991571,0.798252,0.199874]

Compute a 95% confidence interval for each marginal.

[24]:

thetaPosterior = calibrationResult.getParameterPosterior()
alpha = 0.95
dim = thetaPosterior.getDimension()
for i in range(dim):
    print(thetaPosterior.getMarginal(i).computeBilateralConfidenceInterval(alpha))

[1.4721, 1.514]
[0.969123, 1.02096]
[0.794538, 0.802743]
[0.199868, 0.199879]

[25]:

mypcr = CalibrationAnalysis(calibrationResult,calibrationFunction, observedInput, observedOutput)

[26]:

_ = mypcr.drawObservationsVsInputs()

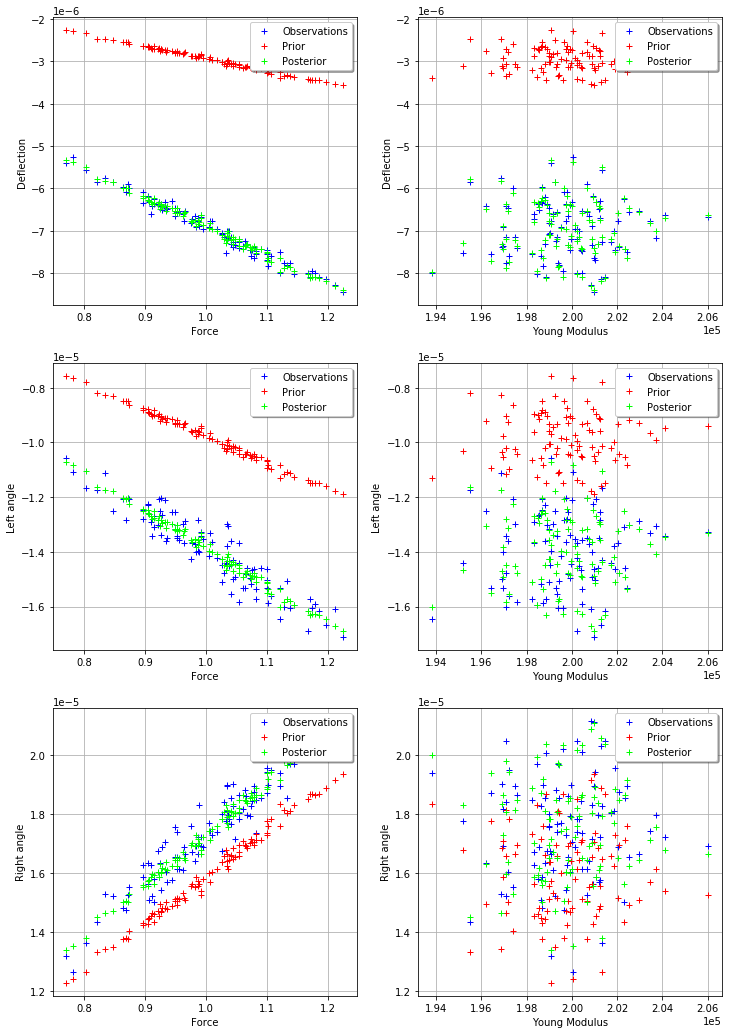
../../_images/examples_calibration_calibration_deflection_tube_35_0.png

[27]:

_ = mypcr.drawObservationsVsPredictions()

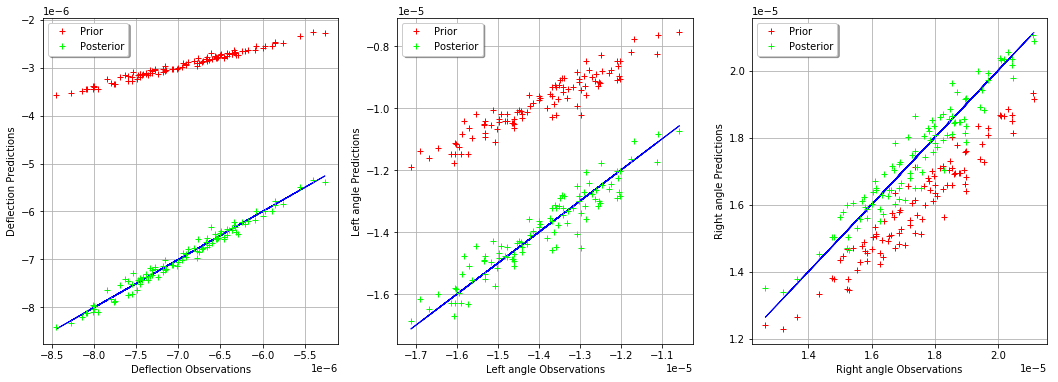
../../_images/examples_calibration_calibration_deflection_tube_36_0.png

[28]:

_ = mypcr.drawResiduals()

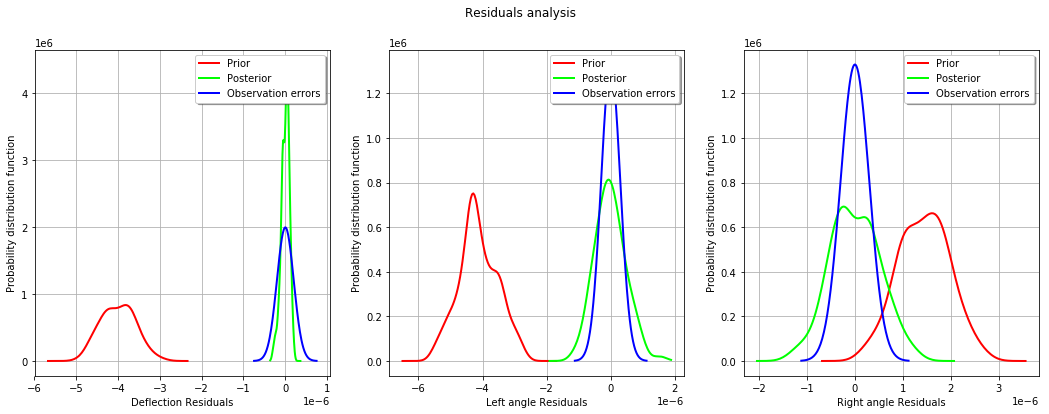
../../_images/examples_calibration_calibration_deflection_tube_37_0.png

[29]:

_ = mypcr.drawParameterDistributions()

../../_images/examples_calibration_calibration_deflection_tube_38_0.png

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Table of Contents

Previous topic

Next topic

This Page