Correlation analysis on samples

In this example we are going to estimate the correlation between an output sample Y and the corresponding inputs using various estimators:

  • Pearson coefficients

  • Spearman coefficients

  • PCC: Partial Correlation Coefficients

  • PRCC: Partial Rank Correlation Coefficient

  • SRC: Standard Regression Coefficients

  • SRRC: Standard Rank Regression Coefficient

[1]:

from __future__ import print_function
import openturns as ot

To illustrate the usage of the method mentionned above, we define a set of X/Y data using the ususal Ishigami use-case.

[2]:

# Create X/Y data
ot.RandomGenerator.SetSeed(0)
formula = ['X3+sin(pi_*X1)+7*sin(X2)*sin(pi_*X2)+' + \
           '1.2*((pi_*X3)*(pi_*X2))*sin(pi_*X1)']
input_names = ['X1', 'X2', 'X3']
model = ot.SymbolicFunction(input_names, formula)
distribution = ot.ComposedDistribution([ot.Uniform(-1.0, 1.0)] * 3, \
                                        ot.IndependentCopula(3))
size = 100
inputDesign = ot.SobolIndicesExperiment(distribution, size, True).generate()
outputDesign = model(inputDesign)

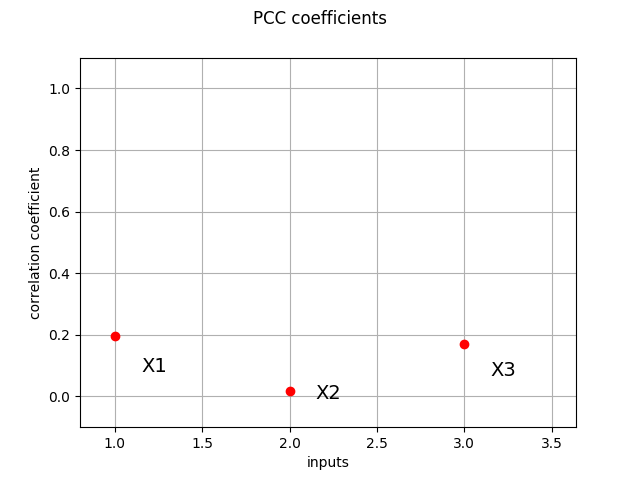
PCC coefficients

We compute here PCC coefficients using the CorrelationAnalysis

[3]:

pcc_indices = ot.CorrelationAnalysis.PCC(inputDesign, outputDesign)
print(pcc_indices)

[0.195052,0.0183082,0.171376]

[4]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(pcc_indices, input_names, "PCC coefficients")

[4]:
../../_images/examples_data_analysis_sample_correlation_8_0.png

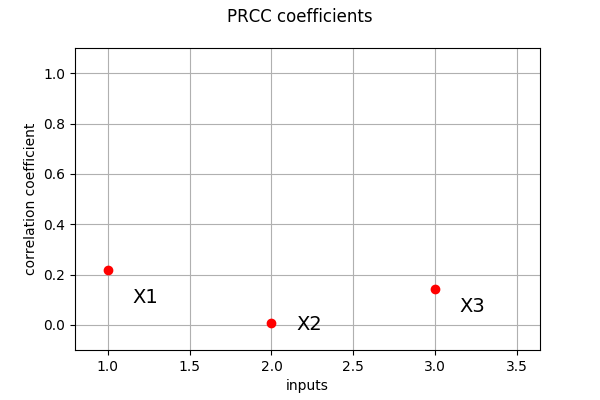
PRCC coefficients

We compute here PRCC coefficients using the CorrelationAnalysis

[5]:

prcc_indices = ot.CorrelationAnalysis.PRCC(inputDesign, outputDesign)
print(prcc_indices)

[0.218657,0.00540221,0.14355]

[6]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(prcc_indices, input_names, "PRCC coefficients")

[6]:
../../_images/examples_data_analysis_sample_correlation_11_0.png

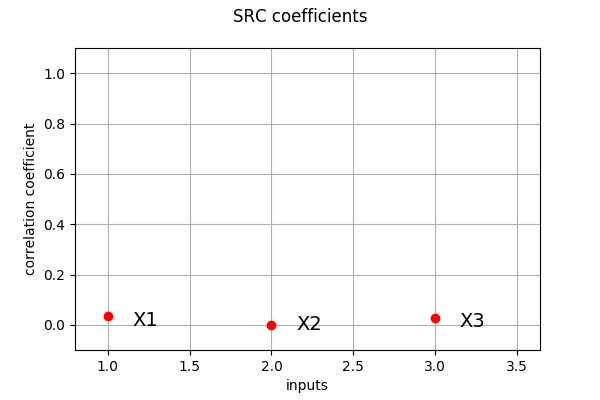
SRC coefficients

We compute here SRC coefficients using the CorrelationAnalysis

[7]:

src_indices = ot.CorrelationAnalysis.SRC(inputDesign, outputDesign)
print(src_indices)

[0.0369391,0.000313641,0.0282987]

[8]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(src_indices, input_names, 'SRC coefficients')

[8]:
../../_images/examples_data_analysis_sample_correlation_14_0.png

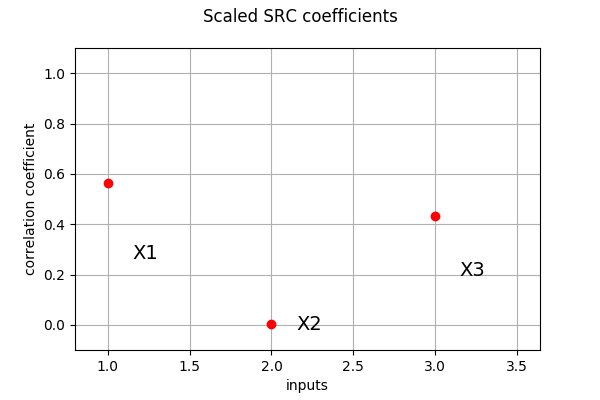
Case where coefficients sum to 1 :

[9]:

scale_src_indices = ot.CorrelationAnalysis.SRC(inputDesign, outputDesign, True)
print(scale_src_indices)

[0.563513,0.00478466,0.431703]

And its associated graph:

[10]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(scale_src_indices, input_names, 'Scaled SRC coefficients')

[10]:
../../_images/examples_data_analysis_sample_correlation_18_0.png

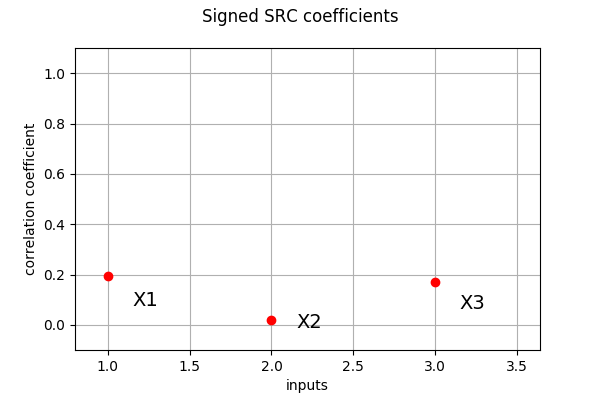
Finally, using signed src: we get the trend importance :

[11]:

signed_src_indices = ot.CorrelationAnalysis.SignedSRC(inputDesign, outputDesign)
print(signed_src_indices)

[0.192195,0.0177099,0.168222]

and its graph :

[12]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(signed_src_indices, input_names, 'Signed SRC coefficients')

[12]:
../../_images/examples_data_analysis_sample_correlation_22_0.png

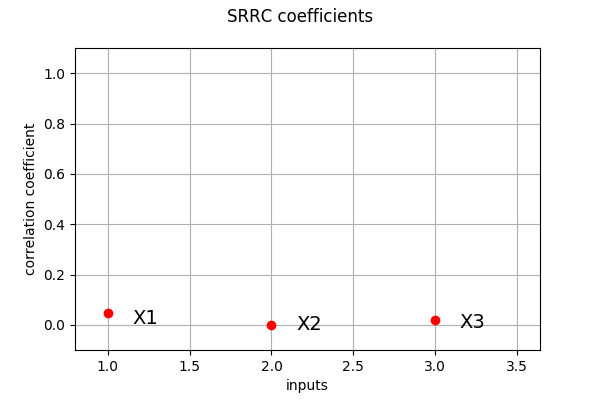
SRRC coefficients

We compute here SRRC coefficients using the CorrelationAnalysis

[13]:

srrc_indices = ot.CorrelationAnalysis.SRRC(inputDesign, outputDesign)
print(srrc_indices)

[0.0468524,2.72779e-05,0.0196627]

[14]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(srrc_indices, input_names, 'SRRC coefficients')

[14]:
../../_images/examples_data_analysis_sample_correlation_26_0.png

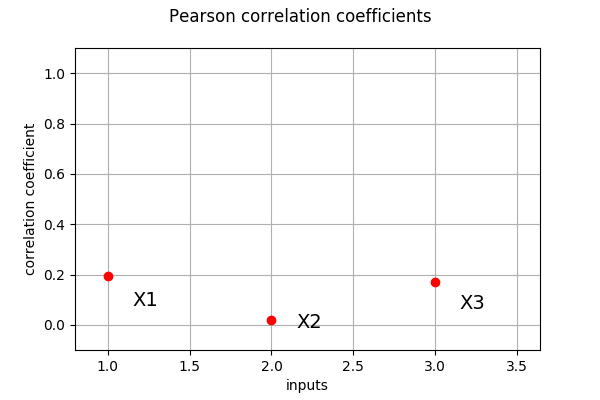
Pearson coefficients

We compute here the Pearson \rho coefficients using the CorrelationAnalysis

[15]:

pearson_correlation = ot.CorrelationAnalysis.PearsonCorrelation(inputDesign, outputDesign)
print(pearson_correlation)

[0.194078,0.0210564,0.171476]

[16]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(pearson_correlation,
                                                     input_names,
                                                     "Pearson correlation coefficients")

[16]:
../../_images/examples_data_analysis_sample_correlation_29_0.png

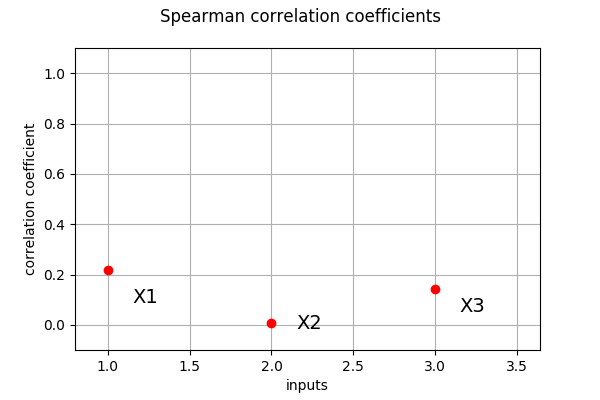
Spearman coefficients

We compute here the Pearson \rho_s coefficients using the CorrelationAnalysis

[17]:

spearman_correlation = ot.CorrelationAnalysis.SpearmanCorrelation(inputDesign, outputDesign)
print(spearman_correlation)

[0.218318,0.00733303,0.143473]

[18]:

ot.SobolIndicesAlgorithm.DrawCorrelationCoefficients(spearman_correlation,
                                                     input_names,
                                                     "Spearman correlation coefficients")

[18]:
../../_images/examples_data_analysis_sample_correlation_32_0.png