Create a discrete Markov chain processΒΆ

This example details first how to create and manipulate a discrete Markov chain.

A discrete Markov chain X: \Omega \times \mathcal{D} \rightarrow E, where E = [\![ 0,...,p-1]\!] is a process where \mathcal{D}=\mathbb{R} discretized on the time grid (t_k)_{k \geq 0} such that:

\begin{aligned} \forall k > 0,\: \mathbb{P} ( X_{t_k} \> | \> X_{t_0},...X_{t_{k-1}} ) = \mathbb{P} ( X_{t_k} \> | \> X_{t_{k-1}} ) \end{aligned}

The transition matrix of the process \mathcal{M} = (m_{i,j}) can be defined such that:

\begin{aligned} \forall t_k \in \mathcal{D}, \forall i,j < p , \> m_{i+1,j+1} = \mathbb{P} (X_{t_{k+1}} = j \> | \> X_{t_{k}} = i) \end{aligned}

The library proposes to model it through the object DiscreteMarkovChain defined thanks to the origin X_{t_0} (which can be either deterministic or uncertain), the transition matrix \mathcal{M} and the time grid.

[1]:

from __future__ import print_function
import openturns as ot

[2]:

# Define the origin
origin = ot.Dirac(0.0)

[3]:

# Define the transition matrix
transition = ot.SquareMatrix([[0.1, 0.3, 0.6], [0.7, 0.1, 0.2], [0.5, 0.3, 0.2]])

[4]:

# Define an 1-d mesh
tgrid = ot.RegularGrid(0.0, 1.0, 50)

[5]:

# Markov chain definition and realization
process = ot.DiscreteMarkovChain(origin, transition, tgrid)
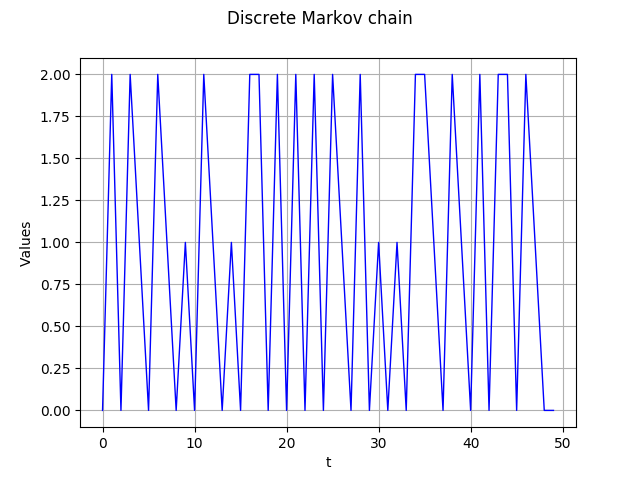
real = process.getRealization()
graph = real.drawMarginal(0)
graph.setTitle('Discrete Markov chain')
graph

[5]:
../../_images/examples_probabilistic_modeling_discrete_markov_chain_process_6_0.png 
[6]:

# Get several realizations
process.setTimeGrid(ot.RegularGrid(0.0,1.0,20))
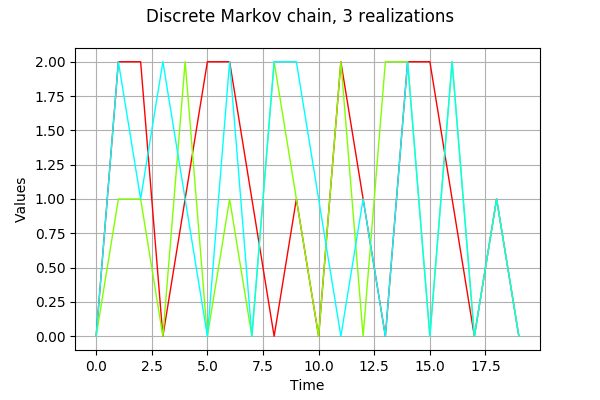
reals = process.getSample(3)
graph = reals.drawMarginal(0)
graph.setTitle('Discrete Markov chain, 3 realizations')
graph

[6]:
../../_images/examples_probabilistic_modeling_discrete_markov_chain_process_7_0.png 
[7]:

# Markov chain future 10 steps
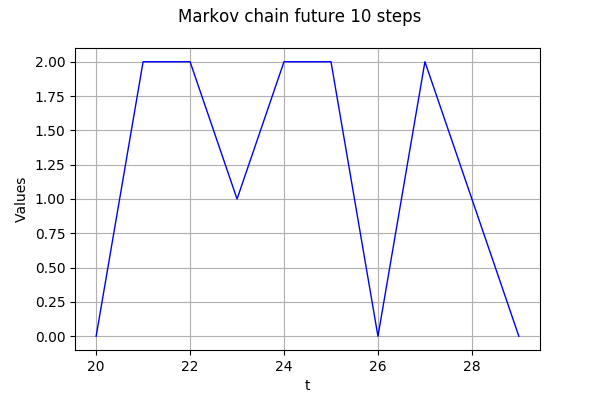
future = process.getFuture(10)
graph = future.drawMarginal(0)
graph.setTitle('Markov chain future 10 steps')
graph

[7]:
../../_images/examples_probabilistic_modeling_discrete_markov_chain_process_8_0.png 
[8]:

# Markov chain 3 different futures
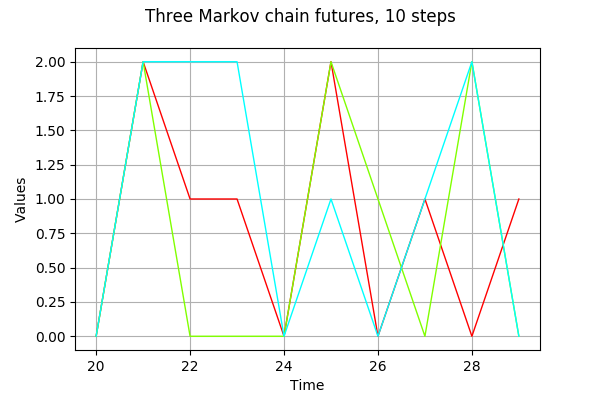
futures = process.getFuture(10,3)
graph = futures.drawMarginal(0)
graph.setTitle('Three Markov chain futures, 10 steps')
graph

[8]:
../../_images/examples_probabilistic_modeling_discrete_markov_chain_process_9_0.png