Field manipulationΒΆ

The objective here is to create and manipulate a field. A field is the agregation of a mesh \mathcal{M} of a domain \mathcal{D} \in \mathbb{R}^n and a sample of values in \mathbb{R}^d associated to each vertex of the mesh.

We note (\underline{t}_0, \dots, \underline{t}_{N-1}) the vertices of \mathcal{M} and (\underline{x}_0, \dots, \underline{x}_{N-1}) the associated values in \mathbb{R}^d.

A field is stored in the Field object that stores the mesh and the values at each vertex of the mesh. It can be built from a mesh and values or as a realization of a stochastic process.

[2]:

from __future__ import print_function
import openturns as ot
import math as m

[4]:

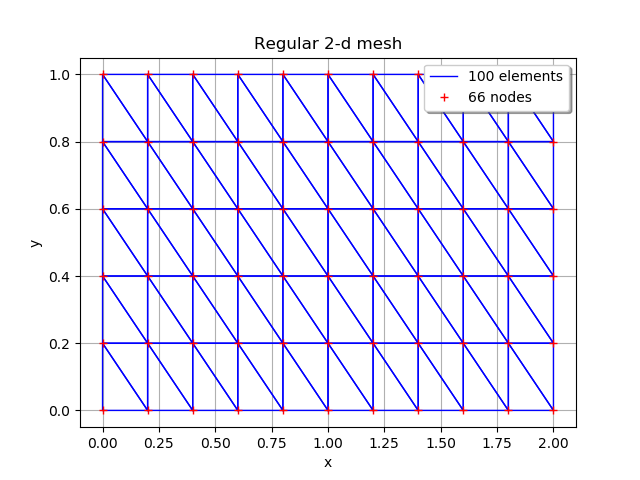
# First, define a regular 2-d mesh
discretization = [10, 5]
mesher = ot.IntervalMesher(discretization)
lowerBound = [0.0, 0.0]
upperBound = [2.0, 1.0]
interval = ot.Interval(lowerBound, upperBound)
mesh = mesher.build(interval)
graph = mesh.draw()
graph.setTitle('Regular 2-d mesh')
graph

[4]:
../../_images/examples_probabilistic_modeling_field_manipulation_3_0.png 
[37]:

# Create a field as a realization of a process
amplitude = [1.0]
scale = [0.2]*2
myCovModel = ot.ExponentialModel(scale, amplitude)
myProcess = ot.GaussianProcess(myCovModel, mesh)
field = myProcess.getRealization()

[6]:

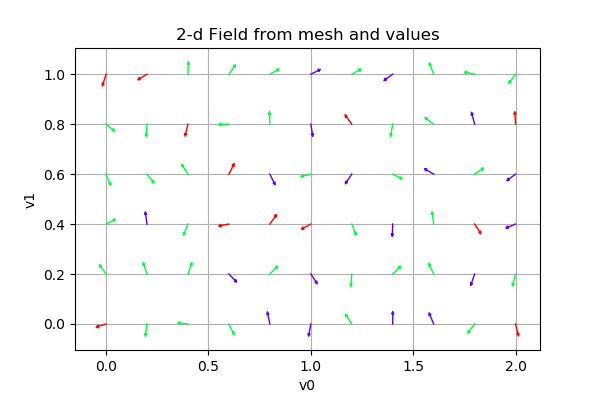
# Create a field from a mesh and some values
values = ot.Normal([0.0]*2, [1.0]*2, ot.CorrelationMatrix(2)).getSample(len(mesh.getVertices()))
for i in range(len(values)):
    x = values[i]
    values[i] = 0.05 * x / x.norm()
field = ot.Field(mesh, values)
graph = field.draw()
graph.setTitle('Field on 2-d mesh and 2-d values')
graph

[6]:
../../_images/examples_probabilistic_modeling_field_manipulation_5_0.png 
[39]:

# Compute the input mean of the field
field.getInputMean()

[39]:

[-0.000900458,0.00189042]

[7]:

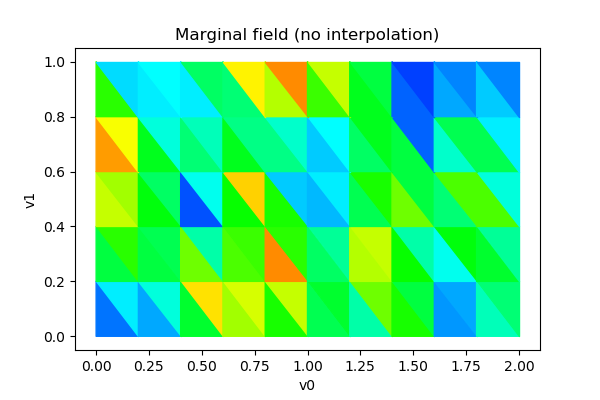
# Draw the field without interpolation
graph = field.drawMarginal(0, False)
graph.setTitle('Marginal field (no interpolation)')
graph

[7]:
../../_images/examples_probabilistic_modeling_field_manipulation_7_0.png 
[8]:

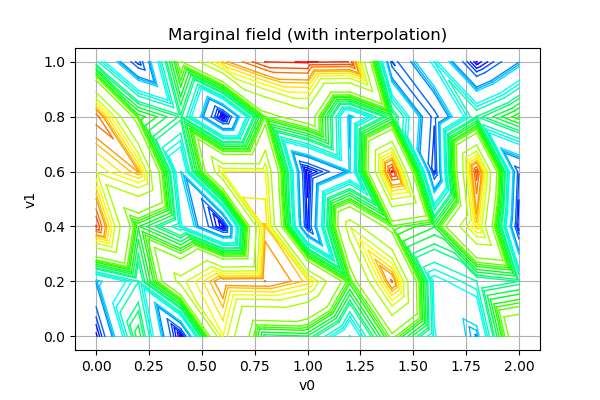
# Draw the field with interpolation
graph = field.drawMarginal(0)
graph.setTitle('Marginal field (with interpolation)')
graph

[8]:
../../_images/examples_probabilistic_modeling_field_manipulation_8_0.png 
[9]:

# Deform the mesh from the field according to the values of the field
# The dimension of the mesh (ie of its vertices) must be the same as the dimension of the field (ie its values)
graph = field.asDeformedMesh().draw()
graph.setTitle('Deformed 2-d mesh')
graph

[9]:
../../_images/examples_probabilistic_modeling_field_manipulation_9_0.png 
[43]:

# Export to the VTK format
field.exportToVTKFile('field.vtk')
with open('field.vtk') as f:
    print(f.read()[:100])

# vtk DataFile Version 3.0
Unnamed
ASCII

DATASET UNSTRUCTURED_GRID
POINTS 66 float
0 0 0.0
0.2 0 0.