Process sample manipulation¶

The objective here is to create and manipulate a process sample. A process sample is a collection of fields which share the same mesh $\mathcal{M} \in \mathbb{R}^n$ .

A process sample can be obtained as $K$ realizations of a multivariate stochastic process $X: \Omega \times \mathcal{D} \rightarrow \mathbb{R}^d$ of dimension $d$ where $\mathcal{D} \in \mathbb{R}^n$ , when the realizations are discretized on the same mesh $\mathcal{M}$ of $\mathcal{D}$ . The values $(\underline{x}_0^k, \dots, \underline{x}_{N-1}^k)$ of the field $k$ are defined by:

$\forall i \in [0, N-1],\quad \underline{x}_i= X(\omega_k)(\underline{t}_i)$

[1]:

from __future__ import print_function
import openturns as ot
import math as m

[2]:

# First, define a regular 2-d mesh
discretization = [10, 5]
mesher = ot.IntervalMesher(discretization)
lowerBound = [0.0, 0.0]
upperBound = [2.0, 1.0]
interval = ot.Interval(lowerBound, upperBound)
mesh = mesher.build(interval)
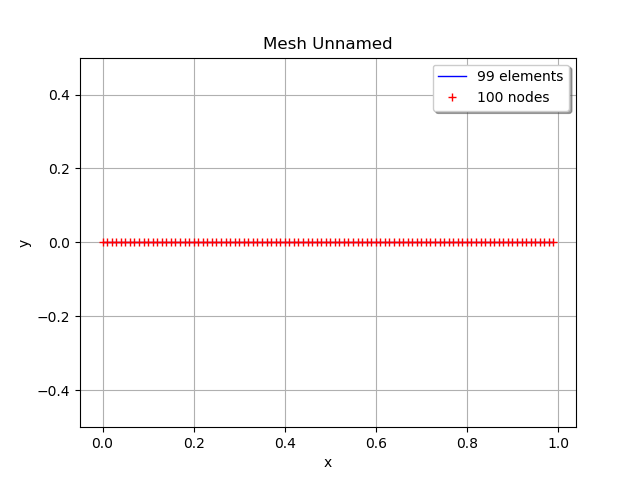
mesh = ot.RegularGrid(0.0, 0.01, 100)
mesh.draw()

[2]:

../../_images/examples_probabilistic_modeling_processsample_manipulation_3_0.png

[3]:

# Allocate a process sample from a field
field = ot.Field()
sampleSize = 10
processSample = ot.ProcessSample(sampleSize, field)
#field.draw()

[15]:

# Create a process sample as realizations of a process
amplitude = [1.0]
scale = [0.2]*1
myCovModel = ot.ExponentialModel(scale, amplitude)
myProcess = ot.GaussianProcess(myCovModel, mesh)
processSample = myProcess.getSample(10)
processSample

[15]:

	t	y0	y0	...	y0	y0	y0
0	0.0	0.18204541662690635	-1.9381887884569047	...	-0.17827621751302086	-0.8225806445605942	0.7555020790891768
1	0.01	0.31693036986975576	-1.6727632838457833	...	-0.6557971110034336	-1.3143923162468978	0.7809459682373394
2	0.02	-0.44012297353381524	-1.8623743139269542	...	-0.6239095486778223	-0.959565076673792	0.740321342937527
...
97	0.97	-0.6348332648437064	0.19979696937503139	...	0.5099518482393706	0.8228505966698729	-1.3885352250532688
98	0.98	-0.830884927448569	-0.07076214982000062	...	0.17679717950155305	1.1805712215667847	-1.559283525482597
99	0.99	-0.7149431051217253	-0.15180096995420744	...	0.13847251025362597	0.7868992309515256	-1.26374605653812

[16]:

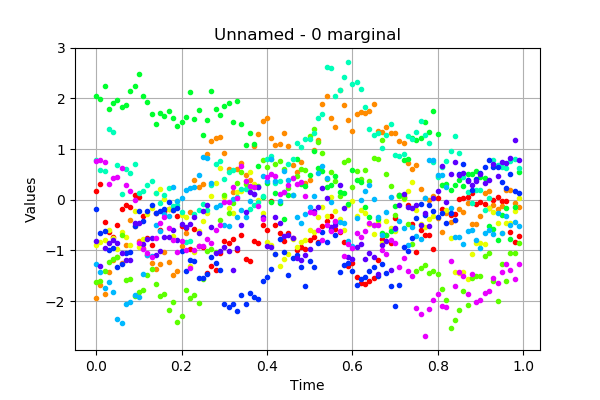
# draw the sample, without interpolation
processSample.drawMarginal(0, False)

[16]:

../../_images/examples_probabilistic_modeling_processsample_manipulation_6_0.png

[6]:

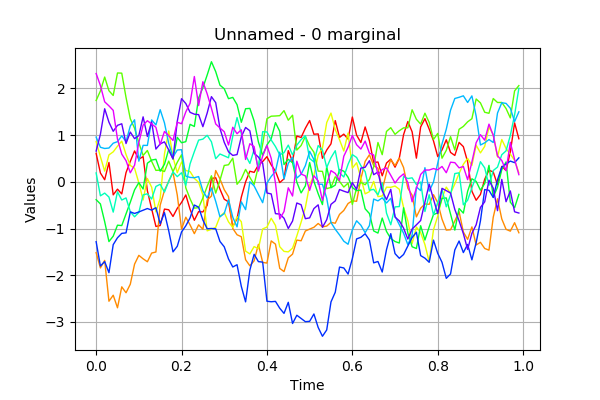
# draw the sample, with interpolation
processSample.drawMarginal(0)

[6]:

../../_images/examples_probabilistic_modeling_processsample_manipulation_7_0.png

[25]:

# Compute the  mean of the process sample
# The result is a field
processSample.computeMean().drawMarginal()

[25]:

	t	y0
0	0.0	-0.2943685746826114
1	0.01	-0.3836675736212855
2	0.02	-0.4280622850739695
3	0.03	-0.38786041728633364
4	0.04	-0.37331752910520494
5	0.05	-0.5147909233972611
6	0.06	-0.4990751669835663
7	0.07	-0.4844038072635097
8	0.08	-0.44069316329972524
9	0.09	-0.24562945712217443
10	0.1	-0.4360868114431804
11	0.11	-0.5328131982827301
12	0.12	-0.4530084660381663
13	0.13	-0.469488376730809
14	0.14	-0.4099617571583579
15	0.15	-0.41990258383255175
16	0.16	-0.291982250584867
17	0.17	-0.3472438491341311
18	0.18	-0.4307719777025618
19	0.19	-0.4828868416664276
20	0.2	-0.5009938406556245
21	0.21	-0.5287747437704691
22	0.22	-0.5957688046485139
23	0.23	-0.40890131390074846
24	0.24	-0.43919452174339774
25	0.25	-0.32379377991846203
26	0.26	-0.19765842954339363
27	0.27	-0.08005206806781928
28	0.28	-0.1390422692790659
29	0.29	-0.011020136448015317
30	0.3	-0.09936335164839094
31	0.31	-0.1935607279056349
32	0.32	-0.20013265916565423
33	0.33	-0.13621884003313167
34	0.34	0.05506396229023293
35	0.35000000000000003	-0.09539426910322614
36	0.36	-0.03046087360049773
37	0.37	0.0358260135077053
38	0.38	-0.02468276317222061
39	0.39	-0.013365079629840827
40	0.4	0.03290530988704926
41	0.41000000000000003	0.09236541265760771
42	0.42	0.008829469357724084
43	0.43	-0.09340391384573817
44	0.44	-0.13022772024938606
45	0.45	-0.11444680788475761
46	0.46	-0.09004564385484443
47	0.47000000000000003	-0.12388845592594633
48	0.48	-0.16908921527982224
49	0.49	-0.23621628297977046
50	0.5	-0.06065877670252251
51	0.51	0.15528900551076183
52	0.52	0.2328522538070708
53	0.53	0.38654325208534185
54	0.54	0.3719318987324228
55	0.55	0.30069502196152453
56	0.56	0.14691883310326911
57	0.5700000000000001	0.1356408550242861
58	0.58	0.07342708661426188
59	0.59	-0.04955297156102289
60	0.6	-0.12172614517980676
61	0.61	-0.05160754498887156
62	0.62	-0.0326774321303532
63	0.63	-0.10668989467443205
64	0.64	-0.15389564561876834
65	0.65	-0.1683840141746808
66	0.66	-0.2358727277844425
67	0.67	-0.2620766456348528
68	0.68	-0.21696536899768884
69	0.6900000000000001	-0.2766349569202509
70	0.7000000000000001	-0.3277948769345407
71	0.71	-0.11736641238444333
72	0.72	0.03680554556822604
73	0.73	-0.1050711014114763
74	0.74	-0.09345092092056338
75	0.75	-0.2765450332422619
76	0.76	-0.3061677367336552
77	0.77	-0.2916400674250887
78	0.78	-0.20597732277551606
79	0.79	-0.15078081190766138
80	0.8	-0.10821960357679204
81	0.81	-0.2546565466130999
82	0.8200000000000001	-0.3989215477491268
83	0.8300000000000001	-0.40253088009985927
84	0.84	-0.5033336522498485
85	0.85	-0.3624046970598575
86	0.86	-0.38363163356005403
87	0.87	-0.4717094074313799
88	0.88	-0.40878538884724347
89	0.89	-0.41833995736628043
90	0.9	-0.3960998494956141
91	0.91	-0.32091340592646284
92	0.92	-0.29185318206573546
93	0.93	-0.2622038632209989
94	0.9400000000000001	-0.347362634575315
95	0.9500000000000001	-0.27233704267043973
96	0.96	-0.205486021227324
97	0.97	-0.25127382136745563
98	0.98	-0.2135784229919815
99	0.99	-0.13558674450100697

[28]:

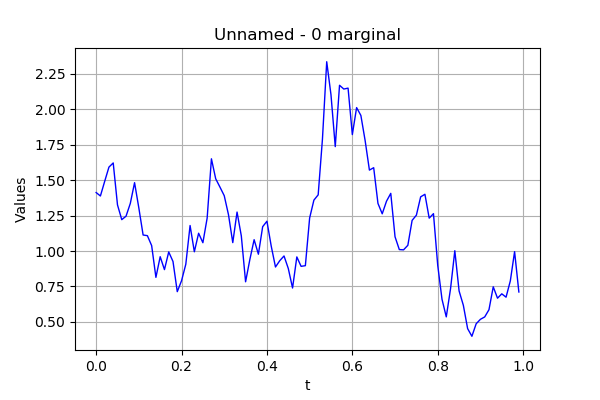
# Draw the quantile field
processSample.computeQuantilePerComponent(0.9).drawMarginal(0)

[28]:

../../_images/examples_probabilistic_modeling_processsample_manipulation_9_0.png

[9]:

# Draw the field with interpolation
processSample.drawMarginal(0)

[9]:

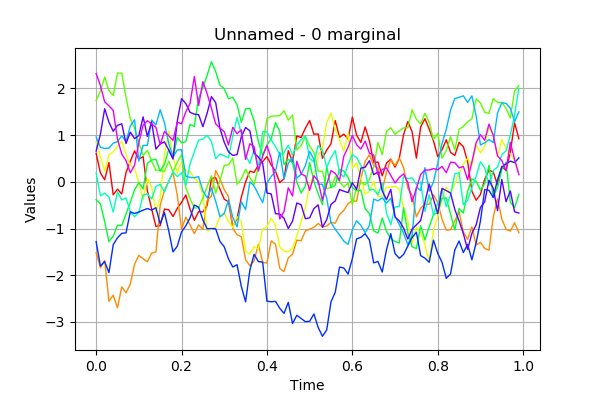
../../_images/examples_probabilistic_modeling_processsample_manipulation_10_0.png

[14]:

processSample

[14]:

	t	y0	y0	...	y0	y0	y0
0	0.0	0.6082016512190991	-1.516964818462452	...	-1.2821033321246131	0.6568188192757204	2.317326540891351
1	0.01	0.18794474534061273	-1.8438198135158375	...	-1.8030765583212214	1.0172101063830876	2.059358992840717
2	0.02	0.043580495738500424	-1.6828293725405234	...	-1.7080610865121886	1.5627428556309622	1.7116099850802056
...
97	0.97	0.6379059880860732	-1.0567978231908535	...	0.44255181856888176	-0.1960842696600071	0.844559444932037
98	0.98	1.2606816514276786	-0.875918616720255	...	0.40963620442024967	-0.6427201575800423	0.47588466080317865
99	0.99	0.9210737505271945	-1.0911123174517658	...	0.5118762676358366	-0.6688705497737476	0.15237663260626474

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

Process sample manipulation¶