Estimate a probability with FORM

In this example we estimate a failure probability with the FORM algorithm on the cantilever beam example. More precisely, we show how to use the associated results:

  • the design point in both physical and standard space,

  • the probability estimation according to the FORM approximation, and the following SORM ones: Tvedt, Hohen-Bichler and Breitung,

  • the Hasofer reliability index and the generalized ones evaluated from the Breitung, Tvedt and Hohen-Bichler approximations,

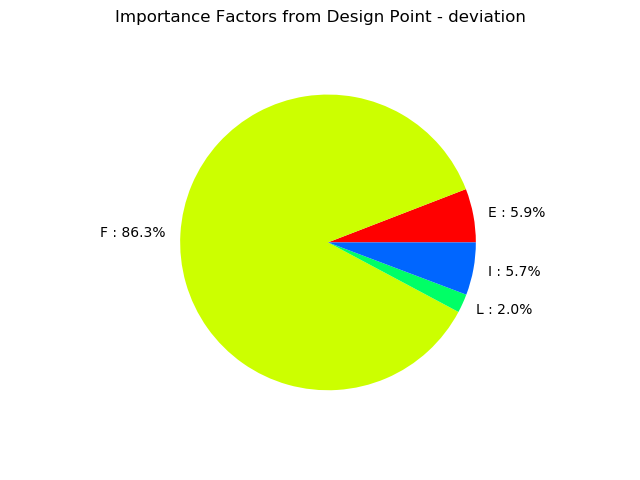
  • the importance factors defined as the normalized director factors of the design point in the U-space

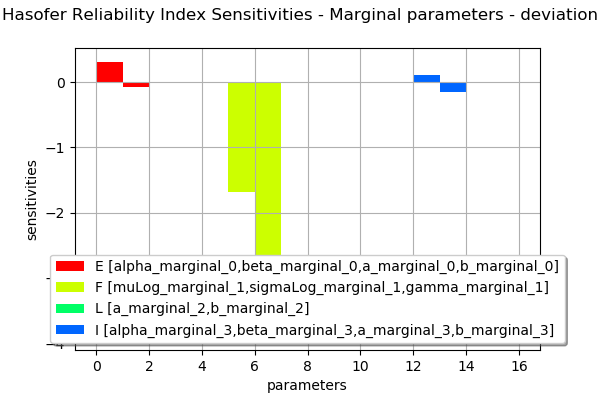
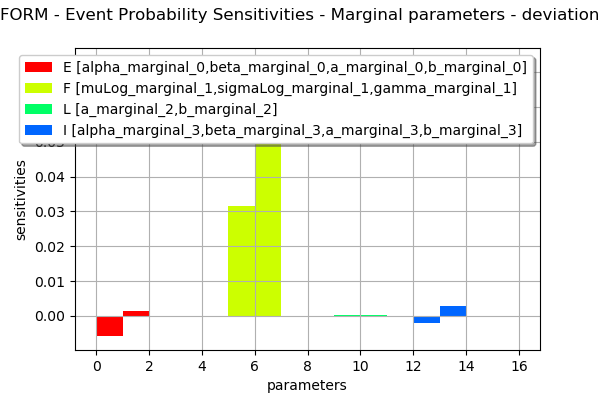
  • the sensitivity factors of the Hasofer reliability index and the FORM probability.

  • the coordinates of the mean point in the standard event space.

The coordinates of the mean point in the standard event space is:

\frac{1}{E_1(-\beta)}\int_{\beta}^{\infty} u_1 p_1(u_1)du_1

where E_1 is the spheric univariate distribution of the standard space and \beta is the reliability index.

Introduction

Let us consider the analytical example of a cantilever beam with Young modulus E, length L and section modulus I.

One end of the cantilever beam is built in a wall and we apply a concentrated bending load F at the other end of the beam, resulting in a deviation:

d = \frac{FL^3}{3EI}

Failure occurs when the beam deviation is too large:

d \ge 30 (cm)

Four independent random variables are considered:

  • E: Young’s modulus [Pa]

  • F: load [N]

  • L: length [m]

  • I: section [m^4]

Stochastic model (simplified model, no units):

  • E ~ Beta(0.93, 2.27, 2.8e7, 4.8e7)

  • F ~ LogNormal(30000, 9000, 15000)

  • L ~ Uniform(250, 260)

  • I ~ Beta(2.5, 1.5, 3.1e2, 4.5e2)

[1]:

from __future__ import print_function
import openturns as ot

Create the marginal distributions of the parameters.

[2]:

dist_E = ot.Beta(0.93, 2.27, 2.8e7, 4.8e7)
dist_F = ot.LogNormalMuSigma(30000, 9000, 15000).getDistribution()
dist_L = ot.Uniform(250, 260)
dist_I = ot.Beta(2.5, 1.5, 3.1e2, 4.5e2)
marginals = [dist_E, dist_F, dist_L, dist_I]

Create the Copula.

[3]:

RS = ot.CorrelationMatrix(4)
RS[2, 3] = -0.2
# Evaluate the correlation matrix of the Normal copula from RS
R = ot.NormalCopula.GetCorrelationFromSpearmanCorrelation(RS)
# Create the Normal copula parametrized by R
copula = ot.NormalCopula(R)

Create the joint probability distribution.

[4]:

distribution = ot.ComposedDistribution(marginals, copula)
distribution.setDescription(['E', 'F', 'L', 'I'])

[5]:

# create the model
model = ot.SymbolicFunction(['E', 'F', 'L', 'I'], ['F*L^3/(3*E*I)'])

Create the event whose probability we want to estimate.

[6]:

vect = ot.RandomVector(distribution)
G = ot.CompositeRandomVector(model, vect)
event = ot.ThresholdEvent(G, ot.Greater(), 30.0)
event.setName("deviation")

[7]:

# Define a solver
optimAlgo = ot.Cobyla()
optimAlgo.setMaximumEvaluationNumber(1000)
optimAlgo.setMaximumAbsoluteError(1.0e-10)
optimAlgo.setMaximumRelativeError(1.0e-10)
optimAlgo.setMaximumResidualError(1.0e-10)
optimAlgo.setMaximumConstraintError(1.0e-10)

[8]:

# Run FORM
algo = ot.FORM(optimAlgo, event, distribution.getMean())
algo.run()
result = algo.getResult()

[9]:

# Probability
result.getEventProbability()

[9]:

0.0067098042649005735

[10]:

# Hasofer reliability index
result.getHasoferReliabilityIndex()

[10]:

2.472435078752308

Design point in the standard U* space.

[11]:

result.getStandardSpaceDesignPoint()

[11]:

[-0.602386,2.31056,0.355794,-0.533677]

Design point in the physical X space.

[12]:

result.getPhysicalSpaceDesignPoint()

[12]:

[3.03272e+07,61318.5,256.39,378.635]

[13]:

# Importance factors
result.drawImportanceFactors()

[13]:
../../_images/examples_reliability_sensitivity_estimate_probability_form_21_0.png 
[14]:

marginalSensitivity, otherSensitivity = result.drawHasoferReliabilityIndexSensitivity()
marginalSensitivity.setLegendPosition('bottom')
marginalSensitivity

[14]:
../../_images/examples_reliability_sensitivity_estimate_probability_form_22_0.png 
[15]:

marginalSensitivity, otherSensitivity = result.drawEventProbabilitySensitivity()
marginalSensitivity

[15]:
../../_images/examples_reliability_sensitivity_estimate_probability_form_23_0.png 
[16]:

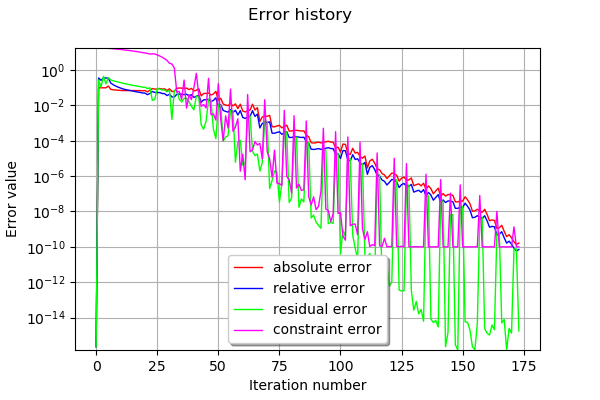
# Error history
optimResult = result.getOptimizationResult()
graphErrors = optimResult.drawErrorHistory()
graphErrors.setLegendPosition('bottom')
graphErrors.setYMargin(0.0)
graphErrors

[16]:
../../_images/examples_reliability_sensitivity_estimate_probability_form_24_0.png 
[17]:

# Get additional results with SORM
algo = ot.SORM(optimAlgo, event, distribution.getMean())
algo.run()
sorm_result = algo.getResult()

[18]:

# Reliability index with Breitung approximation
sorm_result.getGeneralisedReliabilityIndexBreitung()

[18]:

2.5438690625805234

[19]:

# ... with HohenBichler approximation
sorm_result.getGeneralisedReliabilityIndexHohenBichler()

[19]:

2.551468857018457

[20]:

# .. with Tvedt approximation
sorm_result.getGeneralisedReliabilityIndexTvedt()

[20]:

2.5536673927473093

[21]:

# SORM probability of the event with Breitung approximation
sorm_result.getEventProbabilityBreitung()

[21]:

0.005481608620853352

[22]:

# ... with HohenBichler approximation
sorm_result.getEventProbabilityHohenBichler()

[22]:

0.005363495526287012

[23]:

# ... with Tvedt approximation
sorm_result.getEventProbabilityTvedt()

[23]:

0.005329751365065747