SobolIndicesAlgorithm¶

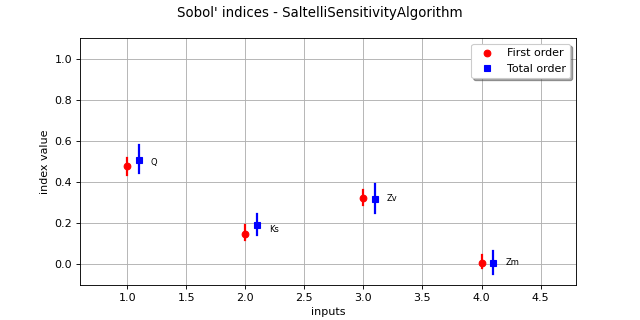
class SobolIndicesAlgorithm(*args)¶

Sensitivity analysis.

Notes

This method is concerned with analyzing the influence the random vector $\vect{X} = \left( X^1, \ldots, X^{n_X} \right)$ has on a random variable $Y^k$ which is being studied for uncertainty (see also [sobol1993]).

Here we attempt to evaluate the part of variance of $Y^k$ due to the different components $X^i$ .

We denote G the physical model such as $\vect{Y}=G(\vect{X})$ . Let us consider first the case where $\vect{Y}$ is of dimension 1.

The objective here is to develop the variability of the random variable $\vect{Y}$ as function of $\vect{X} = \left( X^1, \ldots, X^{n_X} \right)$ . Using the Hoeffding decomposition, we got:

$\Var{\vect{Y}} = \sum_{i=1}^{n_X} V_i + \sum_{i<j} V_{i,j} + \sum_{i<k<j} V_{i,j,k} + \cdots + V_{1,2,..,n_X}$

where :

$V_i = \Var{\Expect{ Y \vert X_i}}$ and $V_{i,j} = \Var{\Expect{ Y \vert X_i, X_j}} - V_i - V_j$ . Using the previous decomposition, it follows that sensitivity indices are defined as follow:

$\begin{array}{ccc} S_i & = & \frac{V_i}{\Var{\vect{Y}}} \\ S_{i,j} & = & \frac{V_{i,j}}{\Var{\vect{Y}}} \end{array}$

$(S_i)$ are the first order sensitivity indices and measure the impact of $X_i$ in the variance $\Var{\vect{Y}}$ , $(S_{i,j})$ are the second order sensitivity indices and measure the impact of the interaction of $X_i$ and $X_j$ in the variance $\Var{\vect{Y}}$ .

When $n_X >> 1$ , we use total sensitivity indices $ST_i$ , which is defined as the sum of all indices that count the i-th variable:

$ST_i = 1 - \frac{V_{-i}}{\Var{\vect{Y}}} = \frac{VT_i}{\Var{\vect{Y}}}, \forall\ i\in(1,2,...,n_X)$

where $V_{-i}$ is the part of variance of $\Var{\vect{Y}}$ that do not countain the i-th variable.

In practice, to estimate these quantities, Sobol proposes to use numerical methods that rely on the two independent realizations of the random vector $\vect{X}$ . If we consider A and B two independent samples (of size n) of the previous random vector:

$A = \left( \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1, n_X} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, n_X} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{1,2} & \cdots & a_{n, n_X} \end{array} \right), \ B = \left( \begin{array}{cccc} b_{1,1} & b_{1,2} & \cdots & b_{1, n_X} \\ b_{2,1} & b_{2,2} & \cdots & b_{2, n_X} \\ \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & b_{1,2} & \cdots & b_{n, n_X} \end{array} \right)$

Each line is a realization of the random vector. The purpose is to mix these two samples to get an estimate of the sensitivities.

Sobol method require respectively $C^i$ and $D^{i,j}$ sample designs for the evaluation of first order (respectively second order) sensitivity indices. These are defined as hereafter:

$C^i = \left( \begin{array}{cccccc} b_{1,1} & b_{1,2} & \cdots & a_{1,i} & \cdots & b_{1, n_X} \\ b_{2,1} & b_{2,2} & \cdots & a_{2,i} & \cdots & b_{2, n_X} \\ \vdots & \vdots & & \vdots & \ddots & \vdots \\ b_{n,1} & b_{1,2} & \cdots & a_{n,i} & \cdots & b_{n, n_X} \end{array} \right), \ D^{i,j} = \left( \begin{array}{cccccccc} b_{1,1} & b_{1,2} & \cdots & a_{1,i} & \cdots & a_{1,j} & \cdots & b_{1, n_X} \\ b_{2,1} & b_{2,2} & \cdots & a_{2,i} & \cdots & a_{2,j} & \cdots & b_{2, n_X} \\ \vdots & \vdots & & \vdots & & \vdots & \ddots & \vdots \\ b_{n,1} & b_{n,2} & \cdots & a_{n,i} & \cdots & a_{n,j} & \cdots & b_{n, n_X} \\ \end{array} \right)$

It follows that $V_{i}$ and $V_{i,j}$ terms are defined as follow:

$\begin{array}{ccc} V_i & = & \frac{1}{n} \sum_{k=1}^{n} G(A_k) G(C_k) - G_0^2 \\ V_{i,j} & = & \frac{1}{n} \sum_{k=1}^{n} G(A_k) G(D_k) - V_i - V_j - G_0^2 \\ G_0 & = & \frac{1}{n} \sum_{k=1}^{n} G(A_k) \end{array}$

The implemented second order indices use this formula.

The major methods (Saltelli, Jansen, Mauntz-Kucherenko, Martinez) use the $E^i$ matrix to compute the indices (first order and total order). This matrix is defined as follows:

$E^i = \left( \begin{array}{cccccc} a_{1,1} & a_{1,2} & \cdots & b_{1,i} & \cdots & a_{1, n_X} \\ a_{2,1} & a_{2,2} & \cdots & b_{2,i} & \cdots & a_{2, n_X} \\ \vdots & \vdots & & \vdots & \ddots & \vdots \\ a_{n,1} & a_{1,2} & \cdots & b_{n,i} & \cdots & a_{n, n_X} \end{array} \right)$

The formulas for the evaluation of the indices are given in each class documentation:

SaltelliSensitivityAlgorithm for the Saltelli method,
JansenSensitivityAlgorithm for the Jansen method,
MauntzKucherenkoSensitivityAlgorithm for the Mauntz-Kucherenko method,
MartinezSensitivityAlgorithm for the Martinez method

For multivariate outputs (see [gamboa2013]), aggregate indices can be computed thanks to the getAggregatedFirstOrderIndices and getAggregatedTotalOrderIndices. Such indices write as follow:

$\begin{array}{ccc} S_i & = & \frac{ \sum_{k=1}^{q} V_{i}^{(k)} }{ \sum_{k=1}^{q} \Var{Y_k} } \\ S_{i,j} & = & \frac{ \sum_{k=1}^{q} V_{i,j}^{(k)} }{ \sum_{k=1}^{q} \Var{Y_k} } \\ ST_i & = & \frac{ \sum_{k=1}^{q} VT_{i}^{(k)} }{ \sum_{k=1}^{q} \Var{Y_k} } \end{array}$

Aggregated second order indices have not been implemented.

Note finally that the distribution of indices can be computed for first and total order thanks to the getFirstOrderIndicesDistribution() and getTotalOrderIndicesDistribution() methods.

This can be done either by bootstrap or using an asymptotic estimator, this behavior can be changed using setUseAsymptoticDistribution(). Its value in initialized by the SobolIndicesAlgorithm-DefaultUseAsymptoticDistribution resourcemap key.

For the bootstrap method the size is set by setBootstrapSize() values and initialized by SobolIndicesAlgorithm-DefaultBootstrapSize resourcemap key.

The asymptotic estimator of the variance are computed using the [janon2014] delta method, in the technical report [pmfre01116].

The corresponding confidence interval is also provided using getFirstOrderIndicesInterval() and getTotalOrderIndicesInterval(). The confidence level is set by setConfidenceLevel and is initialized by the SobolIndicesAlgorithm-DefaultConfidenceLevel resourcemap key.

Also note that for numerical stability reasons the outputs are centered before indices estimation:

$Y_k = Y_k - \Eset(Y_k)$

Methods

`DrawImportanceFactors`(\*args)	Draw the importance factors.
`DrawSobolIndices`(inputDescription, …)	Draw the Sobol’ indices.
`draw`(self, \*args)	Draw sensitivity indices.
`getAggregatedFirstOrderIndices`(self)	Get the evaluation of aggregated first order Sobol indices.
`getAggregatedTotalOrderIndices`(self)	Get the evaluation of aggregated total order Sobol indices.
`getBootstrapSize`(self)	Get the number of bootstrap sampling size.
`getClassName`(self)	Accessor to the object’s name.
`getConfidenceLevel`(self)	Get the confidence interval level for confidence intervals.
`getFirstOrderIndices`(self[, marginalIndex])	Get first order Sobol indices.
`getFirstOrderIndicesDistribution`(self)	Get the distribution of the aggregated first order Sobol indices.
`getFirstOrderIndicesInterval`(self)	Get interval for the aggregated first order Sobol indices.
`getId`(self)	Accessor to the object’s id.
`getImplementation`(self)	Accessor to the underlying implementation.
`getName`(self)	Accessor to the object’s name.
`getSecondOrderIndices`(self[, marginalIndex])	Get second order Sobol indices.
`getTotalOrderIndices`(self[, marginalIndex])	Get total order Sobol indices.
`getTotalOrderIndicesDistribution`(self)	Get the distribution of the aggregated total order Sobol indices.
`getTotalOrderIndicesInterval`(self)	Get interval for the aggregated total order Sobol indices.
`getUseAsymptoticDistribution`(self)	Select asymptotic or bootstrap confidence intervals.
`setBootstrapSize`(self, bootstrapSize)	Set the number of bootstrap sampling size.
`setConfidenceLevel`(self, confidenceLevel)	Set the confidence interval level for confidence intervals.
`setName`(self, name)	Accessor to the object’s name.
`setUseAsymptoticDistribution`(self, …)	Select asymptotic or bootstrap confidence intervals.

DrawCorrelationCoefficients
setDesign

__init__(self, \*args)¶: Initialize self. See help(type(self)) for accurate signature.

static DrawImportanceFactors(\*args)¶

Draw the importance factors.

Available usages:

DrawImportanceFactors(importanceFactors, title=’Importance Factors’)

DrawImportanceFactors(values, names, title=’Importance Factors’)

Parameters

importanceFactorsPointWithDescription: Sequence containing the importance factors with a description for each component. The descriptions are used to build labels for the created Pie. If they are not mentioned, default labels will be used.
valuessequence of float: Importance factors.
namessequence of str: Variables’ names used to build labels for the created Pie.
titlestr: Title of the graph.

Returns

GraphGraph: A graph containing a Pie of the importance factors of the variables.

static DrawSobolIndices(inputDescription, firstOrderIndices, secondOrderIndices)¶

Draw the Sobol’ indices.

Parameters

inputDescriptionsequence of str: Variable names
firstOrderIndicessequence of float: First order indices values
totalOrderIndicessequence of float: Total order indices values

Returns

GraphGraph: For each variable, draws first and total indices

draw(self, \*args)¶

Draw sensitivity indices.

Usage:

draw()

draw(marginalIndex)

With the first usage, draw the aggregated first and total order indices. With the second usage, draw the first and total order indices of a specific marginal in case of vectorial output

Parameters

marginalIndex: int: marginal of interest (case of second usage)

Returns

GraphGraph: A graph containing the aggregated first and total order indices.

Notes

If number of bootstrap sampling is not 0, and confidence level associated > 0, the graph includes confidence interval plots in the first usage.

getAggregatedFirstOrderIndices(self)¶

Get the evaluation of aggregated first order Sobol indices.

Returns

indicesPoint: Sequence containing aggregated first order Sobol indices.

getAggregatedTotalOrderIndices(self)¶

Get the evaluation of aggregated total order Sobol indices.

Returns

indicesPoint: Sequence containing aggregated total order Sobol indices.

getBootstrapSize(self)¶

Get the number of bootstrap sampling size.

Returns

bootstrapSizeint: Number of bootsrap sampling

getClassName(self)¶

Accessor to the object’s name.

Returns

class_namestr: The object class name (object.__class__.__name__).

getConfidenceLevel(self)¶

Get the confidence interval level for confidence intervals.

Returns

confidenceLevelfloat: Confidence level for confidence intervals

getFirstOrderIndices(self, marginalIndex=0)¶

Get first order Sobol indices.

Parameters

iint, optional: Index of the marginal of the function, equals to $0$ by default.

Returns

indicesPoint: Sequence containing first order Sobol indices.

getFirstOrderIndicesDistribution(self)¶

Get the distribution of the aggregated first order Sobol indices.

Returns

distributionDistribution: Distribution for first order Sobol indices for each component.

getFirstOrderIndicesInterval(self)¶

Get interval for the aggregated first order Sobol indices.

Returns

intervalInterval: Interval for first order Sobol indices for each component. Computed marginal by marginal (not from the joint distribution).

getId(self)¶

Accessor to the object’s id.

Returns

idint: Internal unique identifier.

getImplementation(self)¶

Accessor to the underlying implementation.

Returns

implImplementation: The implementation class.

getName(self)¶

Accessor to the object’s name.

Returns

namestr: The name of the object.

getSecondOrderIndices(self, marginalIndex=0)¶

Get second order Sobol indices.

Parameters

iint, optional: Index of the marginal of the function, equals to $0$ by default.

Returns

indicesSymmetricMatrix: Tensor containing second order Sobol indices.

getTotalOrderIndices(self, marginalIndex=0)¶

Get total order Sobol indices.

Parameters

iint, optional: Index of the marginal of the function, equals to $0$ by default.

Returns

indicesPoint: Sequence containing total order Sobol indices.

getTotalOrderIndicesDistribution(self)¶

Get the distribution of the aggregated total order Sobol indices.

Returns

distributionDistribution: Distribution for total order Sobol indices for each component.

getTotalOrderIndicesInterval(self)¶

Get interval for the aggregated total order Sobol indices.

Returns

intervalInterval: Interval for total order Sobol indices for each component. Computed marginal by marginal (not from the joint distribution).

getUseAsymptoticDistribution(self)¶

Select asymptotic or bootstrap confidence intervals.

Returns

useAsymptoticDistributionbool: Whether to use bootstrap or asymptotic intervals

setBootstrapSize(self, bootstrapSize)¶

Set the number of bootstrap sampling size.

Default value is 0.

Parameters

bootstrapSizeint: Number of bootsrap sampling

setConfidenceLevel(self, confidenceLevel)¶

Set the confidence interval level for confidence intervals.

Parameters

confidenceLevelfloat: Confidence level for confidence intervals

setName(self, name)¶

Accessor to the object’s name.

Parameters

namestr: The name of the object.

setUseAsymptoticDistribution(self, useAsymptoticDistribution)¶

Select asymptotic or bootstrap confidence intervals.

Default value is set by the SobolIndicesAlgorithm-DefaultUseAsymptoticDistribution key.

Parameters

useAsymptoticDistributionbool: Whether to use bootstrap or asymptotic intervals

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

SobolIndicesAlgorithm¶