VisualTest_DrawCDFplot

(Source code, png, hires.png, pdf)

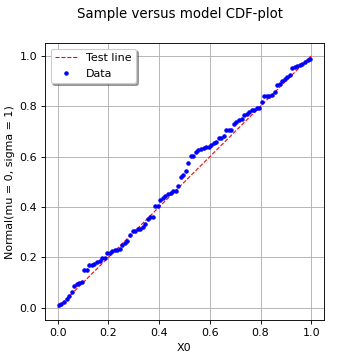
../../_images/VisualTest_DrawCDFplot.png
VisualTest_DrawCDFplot(\*args)

Draw a CDF-plot.

Refer to Using QQ-plot to compare two samples.

Available usages:

VisualTest.DrawCDFplot(sample1, sample2)

VisualTest.DrawCDFplot(sample1, distribution);

Parameters
sample1, sample22-d sequences of float

Tested samples.

ditributionDistribution

Tested model.

Returns
graphclass:~openturns.Graph

The graph object

Notes

The CDF-plot is a visual fitting test for univariate distributions. It opposes the normalized sample ranks to those of the tested quantity (either a distribution or another sample) by plotting the following points cloud:

\left(\dfrac{i+1/2}{m}, F(x^{(i)}) \right), \quad i = 1, \ldots, m

where F denotes either the CDF function of the tested distribution or the empirical CDF of the second tested sample.

If the given sample fits to the tested distribution or sample, then the points should be close to be aligned (up to the uncertainty associated with the estimation of the empirical probabilities) with the first bissector whose equation reads:

y = x, \quad x \in [0,1]

Examples

>>> import openturns as ot
>>> from openturns.viewer import View

Generate a random sample from a Normal distribution:

>>> ot.RandomGenerator.SetSeed(0)
>>> distribution = ot.WeibullMin(2.0, 0.5)
>>> sample = distribution.getSample(30)
>>> sample.setDescription(['Sample'])

Draw a CDF-plot against a given (inferred) distribution:

>>> tested_distribution = ot.WeibullMinFactory().build(sample)
>>> CDF_plot = ot.VisualTest.DrawCDFplot(sample, tested_distribution)
>>> View(CDF_plot).show()

Draw a two-sample CDF-plot:

>>> another_sample = distribution.getSample(50)
>>> another_sample.setDescription(['Another sample'])
>>> CDF_plot = ot.VisualTest.DrawCDFplot(sample, another_sample)
>>> View(CDF_plot).show()