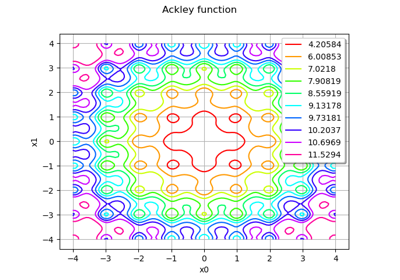
The Ackley test case

Introduction

The Ackley test case is a real function defined in dimension d where d is an integer.

The Ackley function is defined by the equation:

f(\mathbf{x}) = -a \exp\left(-b\sqrt{\frac{1}{d}\sum_{i=1}^d}x_i^2\right)-\exp\left(\frac{1}{d}\sum_{i=1}^d \cos(c x_i)\right)+a+\exp(1)

for any \mathbf{x} \in [-15,15]^d. However, we consider the smaller interval [-4,4]^d in this example, for visual purposes.

We use the dimension d=2 with the parameters a=20, b=0.2, c=2\pi.

The solution is

\mathbf{x}^\star=(0,0,...,0)

where

f_{min} = f(\mathbf{x}^\star) = 0.

References

  • Adorio, E. P., & Diliman, U. P. MVF - Multivariate Test Functions Library in C for Unconstrained Global Optimization (2005). Retrieved June 2013, from http://http://www.geocities.ws/eadorio/mvf.pdf.

  • Molga, M., & Smutnicki, C. Test functions for optimization needs (2005). Retrieved June 2013, from http://www.zsd.ict.pwr.wroc.pl/files/docs/functions.pdf.

  • Back, T. (1996). Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms. Oxford University Press on Demand.

Load the use case

We can load this classical model from the use cases module as follows :

>>> from openturns.usecases import ackley_function as ackley_function
>>> # Load the Ackley model
>>> am = ackley_function.AckleyModel()

API documentation

See AckleyModel.

Examples based on this use case