TensorApproximationAlgorithm

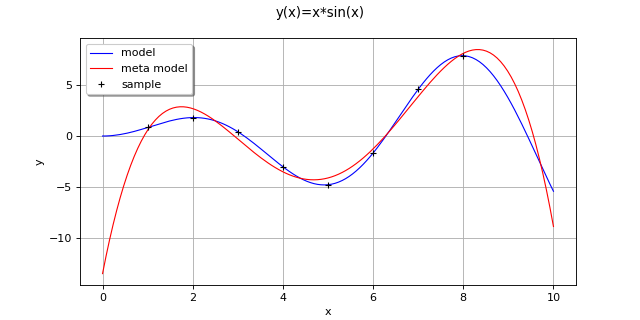
(Source code, png, hires.png, pdf)

../../../_images/TensorApproximationAlgorithm.png
class TensorApproximationAlgorithm(*args)

Tensor approximation algorithm.

Available constructors:

TensorApproximationAlgorithm(inputSample, outputSample, distribution, functionFactory, nk)

Parameters
inputSample, outputSample2-d sequence of float

The input random variables \vect{X}=(X_1, \dots, X_{n_X})^T and the output samples \vect{Y} of a model evaluated apart.

distributionDistribution

Joint probability density function f_{\vect{X}}(\vect{x}) of the physical input vector \vect{X}.

functionFactoryOrthogonalProductFunctionFactory

The basis factory.

degreessequence of int

The size of the basis for each component Of size equal to the input dimension.

maxRankint, optional (default=1)

The maximum rank

See also

FunctionalChaosAlgorithm, KrigingAlgorithm

Notes

TensorApproximationAlgorithm allows to perform a low-rank approximation in the canonical tensor format (refer to [rai2015] for other tensor formats and more details).

The canonical tensor approximation of rank 1 reads:

f(X_1, \dots, X_d) = \prod_{j=1}^d v_j^{(1)} (x_j)

The available alternating least-squares algorithm consists in successive approximations of the coefficients in the basis of the j-th component:

v_j^{(i)} (x_j) = \sum_{k=1}^{n_j} \beta_{j,k}^{(i)} \phi_{j,k} (x_j)

The full canonical tensor approximation of rank m reads:

f(X_1, \dots, X_d) = \sum_{i=1}^m \prod_{j=1}^d v_j^{(i)} (x_j)

The decomposition algorithm can be tweaked using the key TensorApproximationAlgorithm-DecompositionMethod.

Examples

>>> import openturns as ot
>>> dim = 1
>>> f = ot.SymbolicFunction(['x'], ['x*sin(x)'])
>>> uniform = ot.Uniform(0.0, 10.0)
>>> distribution = ot.ComposedDistribution([uniform]*dim)
>>> factoryCollection = [ot.OrthogonalUniVariateFunctionFamily(ot.OrthogonalUniVariatePolynomialFunctionFactory(ot.StandardDistributionPolynomialFactory(uniform)))] * dim
>>> functionFactory = ot.OrthogonalProductFunctionFactory(factoryCollection)
>>> size = 10
>>> sampleX = [[1.0], [2.0], [3.0], [4.0], [5.0], [6.0], [7.0], [8.0]]
>>> sampleY = f(sampleX)
>>> nk = [5] * dim
>>> maxRank = 1
>>> algo = ot.TensorApproximationAlgorithm(sampleX, sampleY, distribution, functionFactory, nk, maxRank)
>>> algo.run()

Get the resulting meta model:

result = algo.getResult() metamodel = result.getMetaModel()

Methods

BuildDistribution(inputSample)

Recover the distribution, with metamodel performance in mind.

getClassName()

Accessor to the object’s name.

getDistribution()

Accessor to the joint probability density function of the physical input vector.

getId()

Accessor to the object’s id.

getInputSample()

Accessor to the input sample.

getMaximumAlternatingLeastSquaresIteration()

Maximum ALS algorithm iteration accessor.

getMaximumRadiusError()

Maximum radius error accessor.

getMaximumResidualError()

Maximum residual error accessor.

getName()

Accessor to the object’s name.

getOutputSample()

Accessor to the output sample.

getResult()

Result accessor.

getShadowedId()

Accessor to the object’s shadowed id.

getVisibility()

Accessor to the object’s visibility state.

hasName()

Test if the object is named.

hasVisibleName()

Test if the object has a distinguishable name.

run()

Compute the response surface.

setDistribution(distribution)

Accessor to the joint probability density function of the physical input vector.

setMaximumAlternatingLeastSquaresIteration(…)

Maximum ALS algorithm iteration accessor.

setMaximumRadiusError(maximumRadiusError)

Maximum radius error accessor.

setMaximumResidualError(maximumResidualError)

Maximum residual error accessor.

setName(name)

Accessor to the object’s name.

setShadowedId(id)

Accessor to the object’s shadowed id.

setVisibility(visible)

Accessor to the object’s visibility state.
__init__(*args)

Initialize self. See help(type(self)) for accurate signature.

static BuildDistribution(inputSample)

Recover the distribution, with metamodel performance in mind.

For each marginal, find the best 1-d continuous parametric model else fallback to the use of a nonparametric one.

The selection is done as follow:

  • We start with a list of all parametric models (all factories)

  • For each model, we estimate its parameters if feasible.

  • We check then if model is valid, ie if its Kolmogorov score exceeds a threshold fixed in the MetaModelAlgorithm-PValueThreshold ResourceMap key. Default value is 5%

  • We sort all valid models and return the one with the optimal criterion.

For the last step, the criterion might be BIC, AIC or AICC. The specification of the criterion is done through the MetaModelAlgorithm-ModelSelectionCriterion ResourceMap key. Default value is fixed to BIC. Note that if there is no valid candidate, we estimate a non-parametric model (KernelSmoothing or Histogram). The MetaModelAlgorithm-NonParametricModel ResourceMap key allows selecting the preferred one. Default value is Histogram

One each marginal is estimated, we use the Spearman independence test on each component pair to decide whether an independent copula. In case of non independence, we rely on a NormalCopula.

Parameters
sampleSample

Input sample.

Returns
distributionDistribution

Input distribution.

getClassName()

Accessor to the object’s name.

Returns
class_namestr

The object class name (object.__class__.__name__).

getDistribution()

Accessor to the joint probability density function of the physical input vector.

Returns
distributionDistribution

Joint probability density function of the physical input vector.

getId()

Accessor to the object’s id.

Returns
idint

Internal unique identifier.

getInputSample()

Accessor to the input sample.

Returns
inputSampleSample

Input sample of a model evaluated apart.

getMaximumAlternatingLeastSquaresIteration()

Maximum ALS algorithm iteration accessor.

Returns
maxALSIterationint

The maximum number of iterations for the alternating least-squares algorithm used for the rank-1 approximation.

getMaximumRadiusError()

Maximum radius error accessor.

Returns
maxRadiusErrorfloat

Convergence criterion on the radius during alternating least-squares algorithm used for the rank-1 approximation.

getMaximumResidualError()

Maximum residual error accessor.

Returns
maxResErrfloat

Convergence criterion on the residual during alternating least-squares algorithm used for the rank-1 approximation.

getName()

Accessor to the object’s name.

Returns
namestr

The name of the object.

getOutputSample()

Accessor to the output sample.

Returns
outputSampleSample

Output sample of a model evaluated apart.

getResult()

Result accessor.

Returns
resultTensorApproximationResult

The result of the approximation.

getShadowedId()

Accessor to the object’s shadowed id.

Returns
idint

Internal unique identifier.

getVisibility()

Accessor to the object’s visibility state.

Returns
visiblebool

Visibility flag.

hasName()

Test if the object is named.

Returns
hasNamebool

True if the name is not empty.

hasVisibleName()

Test if the object has a distinguishable name.

Returns
hasVisibleNamebool

True if the name is not empty and not the default one.

run()

Compute the response surface.

setDistribution(distribution)

Accessor to the joint probability density function of the physical input vector.

Parameters
distributionDistribution

Joint probability density function of the physical input vector.

setMaximumAlternatingLeastSquaresIteration(maximumAlternatingLeastSquaresIteration)

Maximum ALS algorithm iteration accessor.

Parameters
maxALSIterationint

The maximum number of iterations for the alternating least-squares algorithm used for the rank-1 approximation.

setMaximumRadiusError(maximumRadiusError)

Maximum radius error accessor.

Parameters
maxRadiusErrorfloat

Convergence criterion on the radius during alternating least-squares algorithm used for the rank-1 approximation.

setMaximumResidualError(maximumResidualError)

Maximum residual error accessor.

Parameters
maxResErrfloat

Convergence criterion on the residual during alternating least-squares algorithm used for the rank-1 approximation.

setName(name)

Accessor to the object’s name.

Parameters
namestr

The name of the object.

setShadowedId(id)

Accessor to the object’s shadowed id.

Parameters
idint

Internal unique identifier.

setVisibility(visible)

Accessor to the object’s visibility state.

Parameters
visiblebool

Visibility flag.