Create an extreme value distribution

Abstract

In this example we show how to define extreme values distributions.

from __future__ import print_function
import openturns as ot
import openturns.viewer as otv
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

The generalized extreme value distribution (GEV)

The GeneralizedExtremeValue distribution is a family of continuous probability distributions that combine the Gumbel, Frechet and WeibullMax distribution, all extreme value distribution.

We define a generalized extreme value distribution with parameters , and

myDistribution = ot.GeneralizedExtremeValue(0.0, 1.0, 0.0)

The GeneralizedExtremeValue class acts as a proxy class. We can get the actual distribution (Weibull, Frechet or Gumbel) with the getActualDistribution method :

print(myDistribution.getActualDistribution())

Out:

Gumbel(beta = 1, gamma = 0)

For the chosen parameters it is a Gumbel distribution with parameters and .

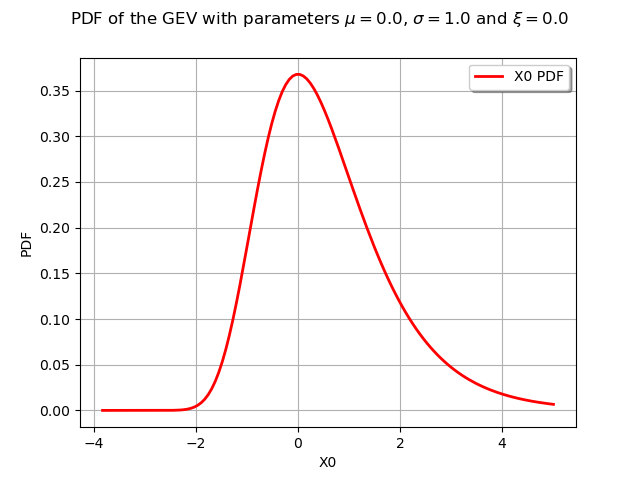
We draw its PDF and CDF :

graphPDF = myDistribution.drawPDF()
graphPDF.setTitle(r"PDF of the GEV with parameters $\mu = 0.0$, $\sigma = 1.0$ and $\xi = 0.0$ ")
view = otv.View(graphPDF)

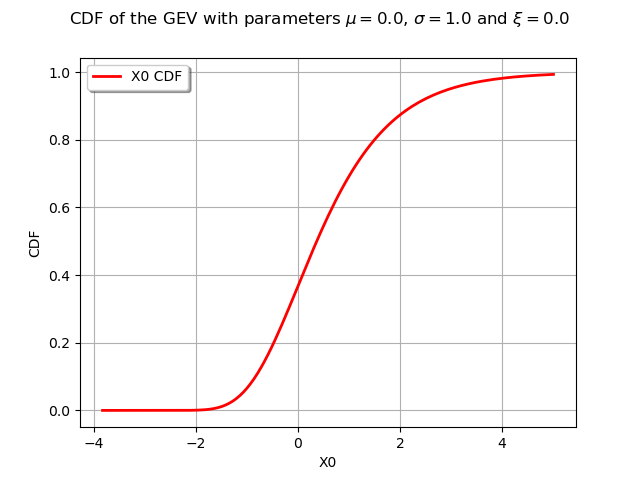
graphCDF = myDistribution.drawCDF()
graphCDF.setTitle(r"CDF of the GEV with parameters $\mu = 0.0$, $\sigma = 1.0$ and $\xi = 0.0$ ")
view = otv.View(graphCDF)

• 
• 

The Generalized Pareto Distribution (GPD)

In this paragraph we turn to the definition of a GeneralizedPareto distribution. For instance we build a generalized Pareto distribution with parameters , and :

myGPD = ot.GeneralizedPareto(1.0, 0.0, 0.0)

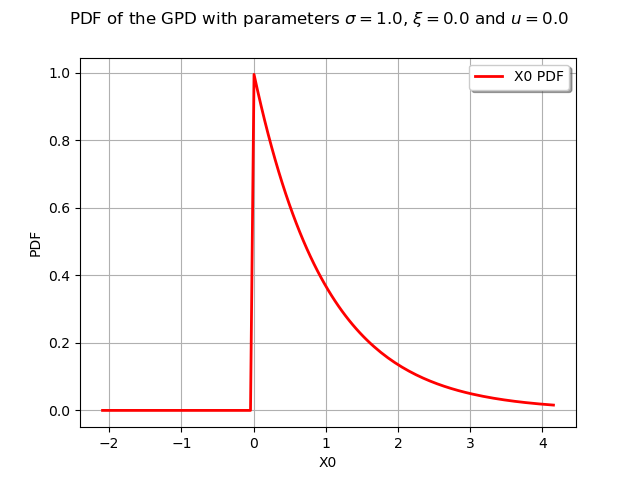
We draw its PDF and CDF :

graphPDF = myGPD.drawPDF()
graphPDF.setTitle(r"PDF of the GPD with parameters $\sigma = 1.0$, $\xi = 0.0$ and $u = 0.0$ ")
view = otv.View(graphPDF)

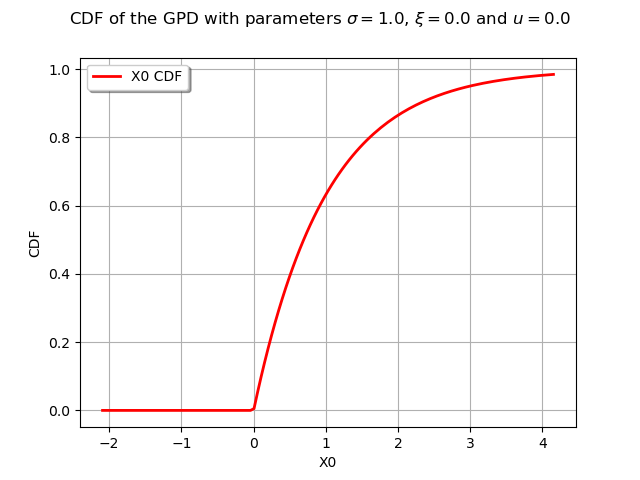
graphCDF = myGPD.drawCDF()
graphCDF.setTitle(r"CDF of the GPD with parameters $\sigma = 1.0$, $\xi = 0.0$ and $u = 0.0$ ")
view = otv.View(graphCDF)

Display all figures

plt.show()