Pearson correlation coefficient¶

This method deals with the parametric modelling of a probability distribution for a random vector $\vect{X} = \left( X^1,\ldots,X^{n_X} \right)$ . It aims to measure a type of dependence (here a linear correlation) which may exist between two components $X^i$ and $X^j$ .

The Pearson’s correlation coefficient $\rho_{U,V}$ aims to measure the strength of a linear relationship between two random variables $U$ and $V$ . It is defined as follows:

$\begin{aligned} \rho_{U,V} = \frac{\displaystyle \Cov{U,V}}{\sigma_U \sigma_V} \end{aligned}$

where $\Cov{U,V} = \Expect{ \left( U - m_U \right) \left( V - m_V \right) }$ , $m_U= \Expect{U}$ , $m_V= \Expect{V}$ , $\sigma_U= \sqrt{\Var{U}}$ and $\sigma_V= \sqrt{\Var{V}}$ . If we have a sample made up of a set of $N$ pairs $\left\{ (u_1,v_1),(u_2,v_2),\ldots,(u_N,v_N) \right\}$ , Pearson’s correlation coefficient can be estimated using the formula:

$\begin{aligned} \widehat{\rho}_{U,V} = \frac{ \displaystyle \sum_{i=1}^N \left( u_i - \overline{u} \right) \left( v_i - \overline{v} \right) }{ \sqrt{\displaystyle \sum_{i=1}^N \left( u_i - \overline{u} \right)^2 \left( v_i - \overline{v} \right)^2} } \end{aligned}$

where $\overline{u}$ and $\overline{v}$ represent the empirical means of the samples $(u_1,\ldots,u_N)$ and $(v_1,\ldots,v_N)$ .

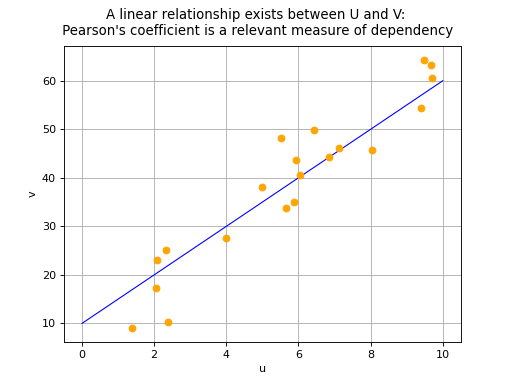
Pearson’s correlation coefficient takes values between -1 and 1. The closer its absolute value is to 1, the stronger the indication is that a linear relationship exists between variables $U$ and $V$ . The sign of Pearson’s coefficient indicates if the two variables increase or decrease in the same direction (positive coefficient) or in opposite directions (negative coefficient). 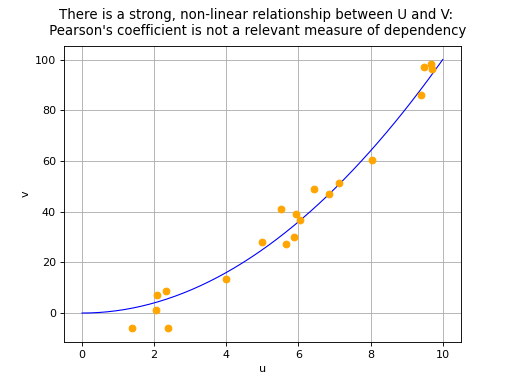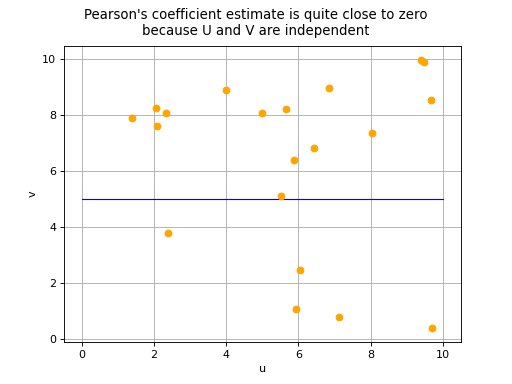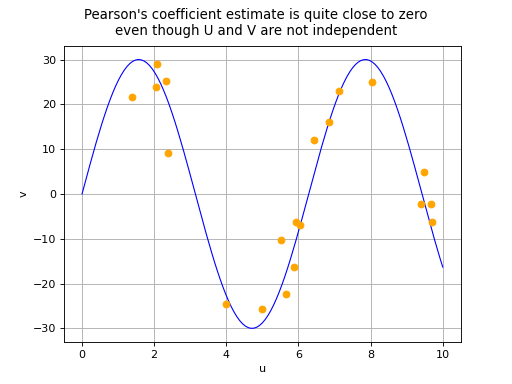We note that a correlation coefficient equal to 0 does not necessarily imply the independence of variables $U$ and $V$ : this property is in fact theoretically guaranteed only if $U$ and $V$ both follow a Normal distribution. In all other cases, there are two possible situations in the event of a zero Pearson’s correlation coefficient: