Vertical deflection of a tube¶
Description¶
We consider the deflection of a tube under a vertical stress.
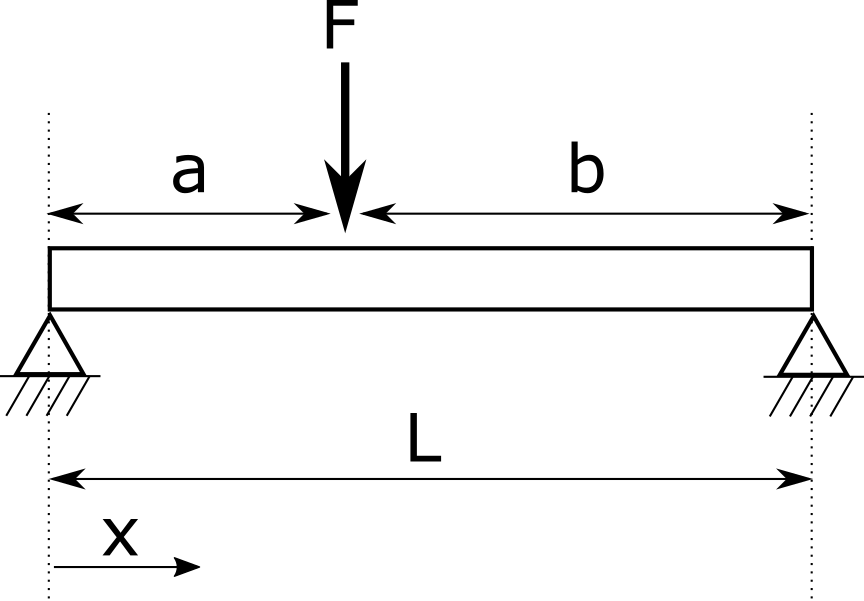
A simply supported beam¶
The parameters of the model are:
F : the strength,
L : the length of the tube,
a : position of the force,
D : external diameter of the tube,
d : internal diameter of the tube,
E : Young modulus.
The following figure presents the internal and external diameter of the tube:

Tube diameters¶
The area moment of inertia of the cross section about the neutral axis of a round tube (i.e. perpendicular to the section) with external and internal diameters and
are:
The vertical deflection at point is:
where .
The angle of the tube at the left end is:
and the angle of the tube at the right end is:
The following table presents the distributions of the random variables. These variables are assumed to be independent.
Variable |
Distribution |
|---|---|
F |
Normal(1,0.1) |
L |
Normal(1.5,0.01) |
a |
Uniform(0.7,1.2) |
D |
Triangular(0.75,0.8,0.85) |
d |
Triangular(0.09,0.1,0.11) |
E |
Normal(200000,2000) |
References¶
Deflection of beams by Russ Elliott. http://www.clag.org.uk/beam.html
https://upload.wikimedia.org/wikipedia/commons/f/ff/Simple_beam_with_offset_load.svg
Shigley’s Mechanical Engineering Design (9th Edition), Richard G. Budynas, J. Keith Nisbettn, McGraw Hill (2011)
Mechanics of Materials (7th Edition), James M. Gere, Barry J. Goodno, Cengage Learning (2009)
Statics and Mechanics of Materials (5th Edition), Ferdinand Beer, E. Russell Johnston, Jr., John DeWolf, David Mazurek. Mc Graw Hill (2011) Chapter 15: deflection of beams.
Load the use case¶
We can load this classical model from the use cases module as follows :
>>> from openturns.usecases import deflection_tube as deflection_tube
>>> # Load the tube deflection model
>>> dt = deflection_tube.DeflectionTube()
API documentation¶
See DeflectionTube.
 OpenTURNS
OpenTURNS