Calibration of the deflection of a tube

We consider a calibration of the deflection of a tube as described here.

import openturns as ot
import openturns.viewer as viewer
from matplotlib import pylab as plt
ot.Log.Show(ot.Log.NONE)

Create a calibration problem

We load the model from the use case module :

from openturns.usecases import deflection_tube as deflection_tube
dt = deflection_tube.DeflectionTube()

We create a sample out of our input distribution :

sampleSize = 100
inputSample = dt.inputDistribution.getSample(sampleSize)
inputSample[0:5]

	Force	Length	Location	External diameter	Internal diameter	Young Modulus
0	0.9172019	1.5	1	0.8	0.1	201371.2
1	0.980412	1.5	1	0.8	0.1	199257.1
2	1.107203	1.5	1	0.8	0.1	201831.9
3	1.059726	1.5	1	0.8	0.1	200776.3
4	0.9138437	1.5	1	0.8	0.1	200931.2

We take the image of our input sample by the model :

outputDeflection = dt.model(inputSample)
outputDeflection[0:5]

	Deflection	Left angle	Right angle
0	-6.294212e-06	-1.258842e-05	1.573553e-05
1	-6.799368e-06	-1.359874e-05	1.699842e-05
2	-7.580733e-06	-1.516147e-05	1.895183e-05
3	-7.293815e-06	-1.458763e-05	1.823454e-05
4	-6.284898e-06	-1.25698e-05	1.571224e-05

observationNoiseSigma = [0.1e-6,0.05e-5,0.05e-5]
observationNoiseCovariance = ot.CovarianceMatrix(3)
for i in range(3):
    observationNoiseCovariance[i,i] = observationNoiseSigma[i]**2

noiseSigma = ot.Normal([0.,0.,0.],observationNoiseCovariance)
sampleObservationNoise = noiseSigma.getSample(sampleSize)
observedOutput = outputDeflection + sampleObservationNoise
observedOutput[0:5]

	Deflection	Left angle	Right angle
0	-6.291812e-06	-1.197505e-05	1.597891e-05
1	-6.746338e-06	-1.423263e-05	1.611792e-05
2	-7.639595e-06	-1.608291e-05	1.940262e-05
3	-7.402455e-06	-1.499955e-05	1.723244e-05
4	-6.222688e-06	-1.303563e-05	1.532097e-05

observedInput = ot.Sample(sampleSize,2)
observedInput[:,0] = inputSample[:,0] # F
observedInput[:,1] = inputSample[:,5] # E
observedInput.setDescription(["Force","Young Modulus"])
observedInput[0:5]

	Force	Young Modulus
0	0.9172019	201371.2
1	0.980412	199257.1
2	1.107203	201831.9
3	1.059726	200776.3
4	0.9138437	200931.2

fullSample = ot.Sample(sampleSize,5)
fullSample[:,0:2] = observedInput
fullSample[:,2:5] = observedOutput
fullSample.setDescription(["Force","Young","Deflection","Left Angle","Right Angle"])
fullSample[0:5]

	Force	Young	Deflection	Left Angle	Right Angle
0	0.9172019	201371.2	-6.291812e-06	-1.197505e-05	1.597891e-05
1	0.980412	199257.1	-6.746338e-06	-1.423263e-05	1.611792e-05
2	1.107203	201831.9	-7.639595e-06	-1.608291e-05	1.940262e-05
3	1.059726	200776.3	-7.402455e-06	-1.499955e-05	1.723244e-05
4	0.9138437	200931.2	-6.222688e-06	-1.303563e-05	1.532097e-05

graph = ot.VisualTest.DrawPairs(fullSample)
view = viewer.View(graph)

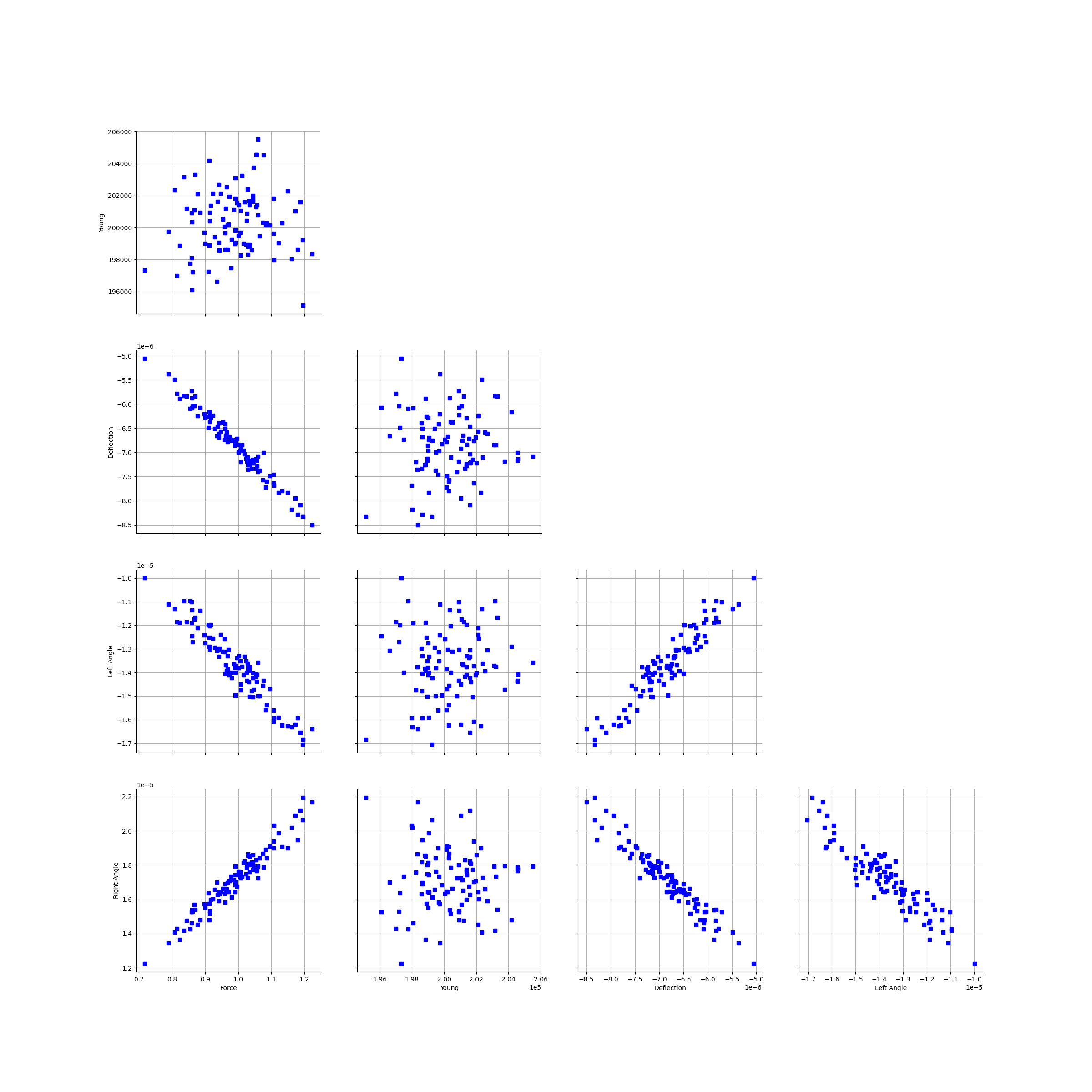
Setting up the calibration

XL = 1.4 # Exact : 1.5
Xa = 1.2 # Exact : 1.0
XD = 0.7 # Exact : 0.8
Xd = 0.2 # Exact : 0.1
thetaPrior = [XL, Xa, XD, Xd]

sigmaXL = 0.1 * XL
sigmaXa = 0.1 * Xa
sigmaXD = 0.1 * XD
sigmaXd = 0.1 * Xd
parameterCovariance = ot.CovarianceMatrix(4)
parameterCovariance[0,0] = sigmaXL**2
parameterCovariance[1,1] = sigmaXa**2
parameterCovariance[2,2] = sigmaXD**2
parameterCovariance[3,3] = sigmaXd**2
parameterCovariance

[[ 0.0196 0 0 0 ]
[ 0 0.0144 0 0 ]
[ 0 0 0.0049 0 ]
[ 0 0 0 0.0004 ]]

calibratedIndices = [1,2,3,4]
calibrationFunction = ot.ParametricFunction(dt.model, calibratedIndices, thetaPrior)

sigmaObservation = [0.2e-6,0.03e-5,0.03e-5] # Exact : 0.1e-6

errorCovariance = ot.CovarianceMatrix(3)
errorCovariance[0,0] = sigmaObservation[0]**2
errorCovariance[1,1] = sigmaObservation[1]**2
errorCovariance[2,2] = sigmaObservation[2]**2

calibrationFunction.setParameter(thetaPrior)
predictedOutput = calibrationFunction(observedInput)
predictedOutput[0:5]

	Deflection	Left angle	Right angle
0	-2.667796e-06	-8.892653e-06	1.445056e-05
1	-2.881906e-06	-9.606352e-06	1.561032e-05
2	-3.213087e-06	-1.071029e-05	1.740422e-05
3	-3.091476e-06	-1.030492e-05	1.67455e-05
4	-2.663848e-06	-8.879493e-06	1.442918e-05

Calibration with gaussian non linear least squares

algo = ot.GaussianNonLinearCalibration(calibrationFunction, observedInput, observedOutput, thetaPrior, parameterCovariance, errorCovariance)

algo.run()

calibrationResult = algo.getResult()

Analysis of the results

thetaMAP = calibrationResult.getParameterMAP()
thetaMAP

[1.50015,1.00142,0.799882,0.19988]

Compute a 95% confidence interval for each marginal.

thetaPosterior = calibrationResult.getParameterPosterior()
alpha = 0.95
dim = thetaPosterior.getDimension()
for i in range(dim):
    print(thetaPosterior.getMarginal(i).computeBilateralConfidenceInterval(alpha))

Out:

[1.48002, 1.52078]
[0.97709, 1.02634]
[0.795846, 0.803887]
[0.199877, 0.199915]

graph = calibrationResult.drawObservationsVsInputs()
view = viewer.View(graph)

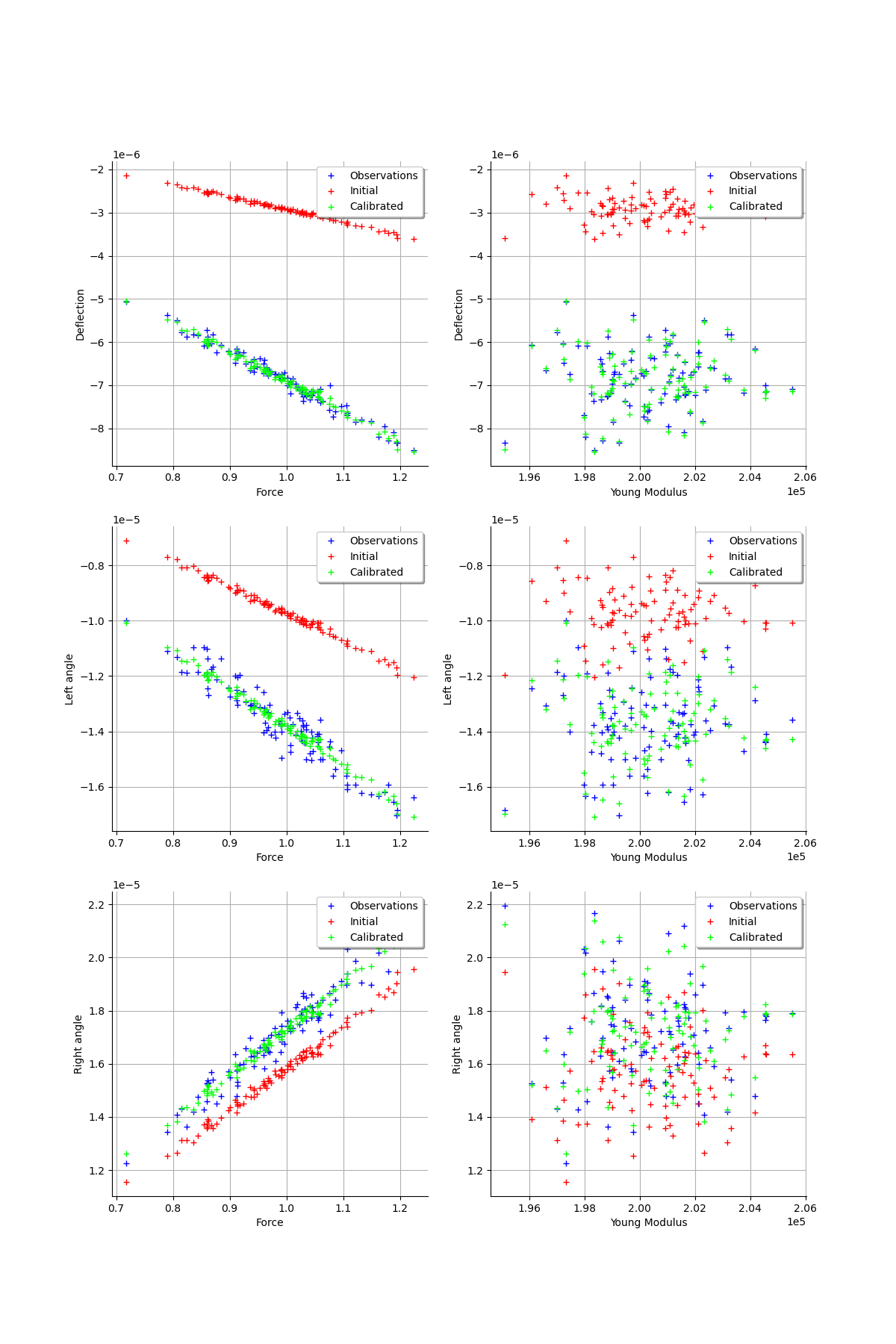
graph = calibrationResult.drawObservationsVsPredictions()
view = viewer.View(graph)

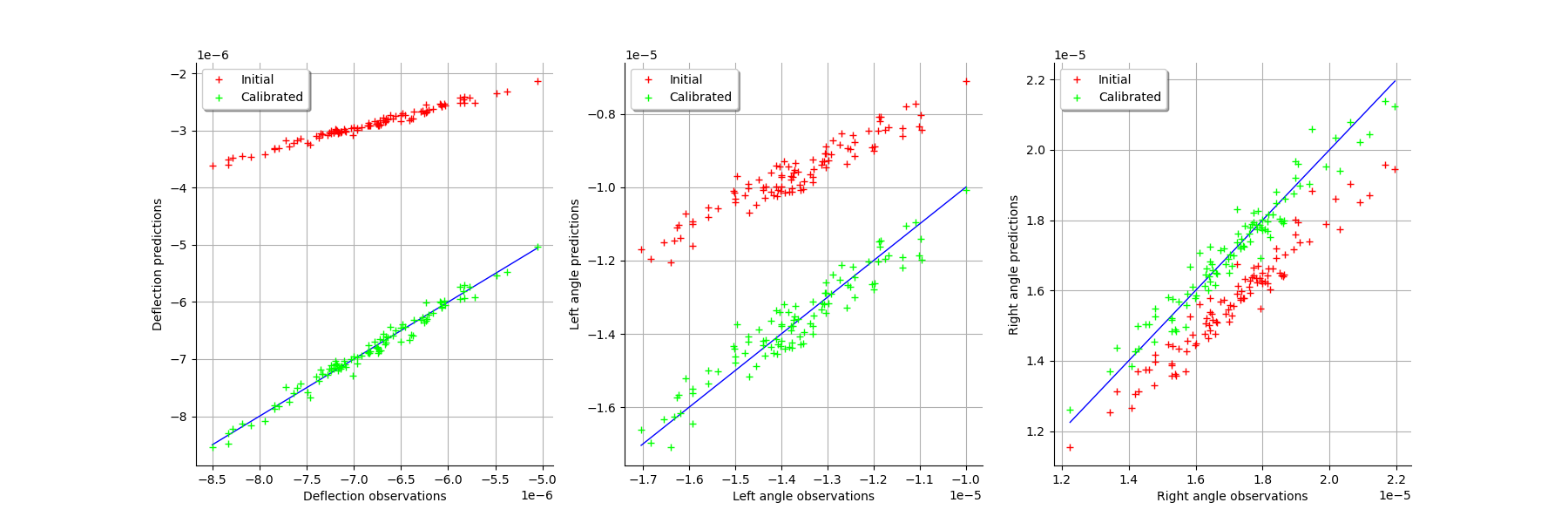
graph = calibrationResult.drawResiduals()
view = viewer.View(graph)

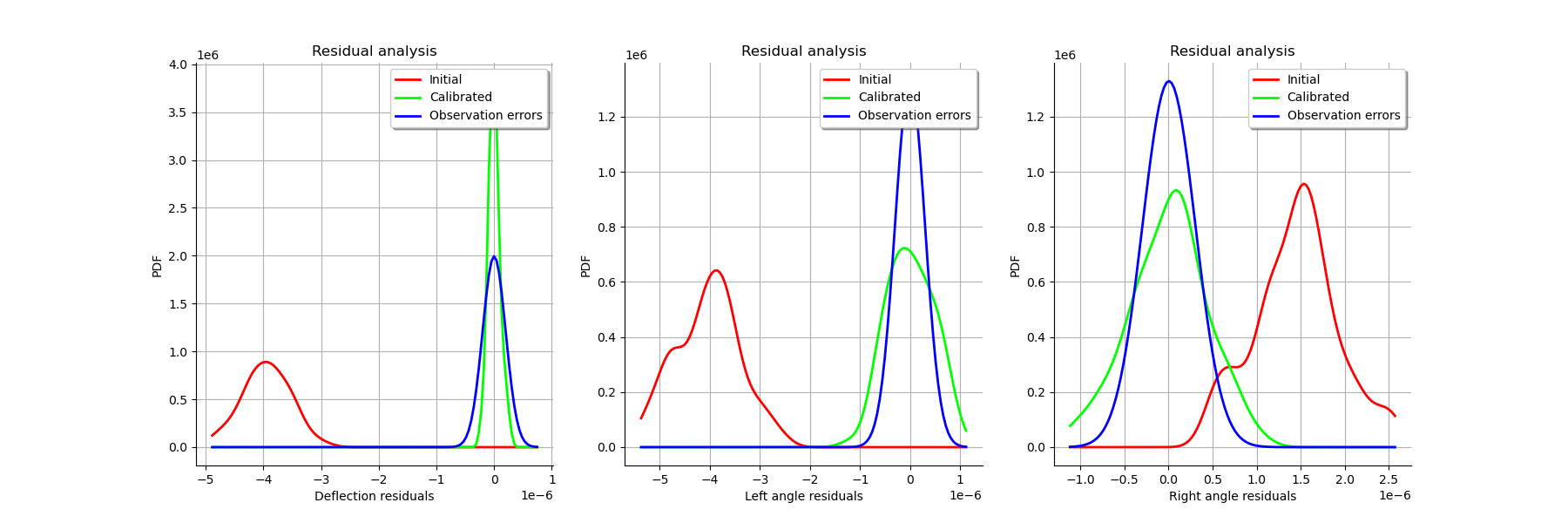
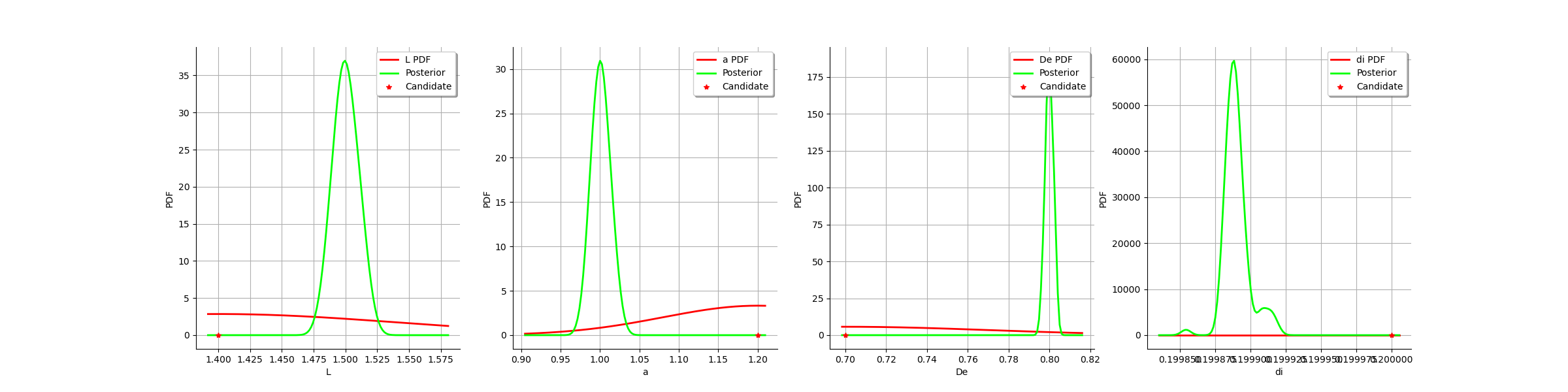
graph = calibrationResult.drawParameterDistributions()
view = viewer.View(graph)

plt.show()