Monte Carlo simulationΒΆ

Using the probability distribution the probability distribution of a random vector \vect{X}, we seek to evaluate the following probability:

P_f = \Prob{g\left( \vect{X},\vect{d} \right) \leq 0}

Here, \vect{X} is a random vector, \vect{d} a deterministic vector, g(\vect{X},\vect{d}) the function known as limit state function which enables the definition of the event \cD_f = \{\vect{X} \in \Rset^n \, / \, g(\vect{X},\vect{d}) \le 0\}.

If we have the set \left\{ \vect{x}_1,\ldots,\vect{x}_N \right\} of N independent samples of the random vector \vect{X}, we can estimate \widehat{P}_f as follows:

\widehat{P}_f = \frac{1}{N} \sum_{i=1}^N \mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} }

where \mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} } describes the indicator function equal to 1 if g(\vect{x}_i,\vect{d}) \leq 0 and equal to 0 otherwise; the idea here is in fact to estimate the required probability by the proportion of cases, among the N samples of \vect{X}, for which the event \cD_f occurs.

By the law of large numbers, we know that this estimation converges to the required value P_f as the sample size N tends to infinity.

The Central Limit Theorem allows one to build an asymptotic confidence interval using the normal limit distribution as follows:

\lim_{N\rightarrow\infty}\Prob{P_f\in[\widehat{P}_{f,\inf},\widehat{P}_{f,\sup}]}=\alpha

with \widehat{P}_{f,\inf}=\widehat{P}_f - q_{\alpha}\sqrt{\frac{\widehat{P}_f(1-\widehat{P}_f)}{N}}$, $\widehat{P}_{f,\sup}=\widehat{P}_f + q_{\alpha}\sqrt{\frac{\widehat{P}_f(1-\widehat{P}_f)}{N}} and q_\alpha is the (1+\alpha)/2-quantile of the standard normal distribution.

One can also use a convergence indicator that is independent of the confidence level $alpha$: the coefficient of variation, which is the ratio between the asymptotic standard deviation of the estimate and its mean value. It is a relative measure of dispersion given by:

\textrm{CV}_{\widehat{P}_f}=\sqrt{ \frac{1-\widehat{P}_f}{N \widehat{P}_f}}\simeq\frac{1}{\sqrt{N\widehat{P}_f}}\mbox{ for }\widehat{P}_f\ll 1

It must be emphasized that these results are asymptotic and as such needs that N\gg 1. The convergence to the standard normal distribution is dominated by the skewness of \mathbf{1}_{ \left\{ g(\vect{x}_i,\vect{d}) \leq 0 \right\} } divided by the sample size N, it means \frac{1-2P_f}{N\sqrt{P_f(1-P_f)}}. In the usual case P_f\ll 1, the distribution is highly skewed and this term is approximately equal to \frac{1}{N\sqrt{P_f}}\simeq\textrm{CV}_{\widehat{P}_f}/\sqrt{N}. A rule of thumb is that if \textrm{CV}_{\widehat{P}_f}<0.1 with N>10^2, the asymptotic nature of the Central Limit Theorem is not problematic.

(Source code, png, hires.png, pdf)

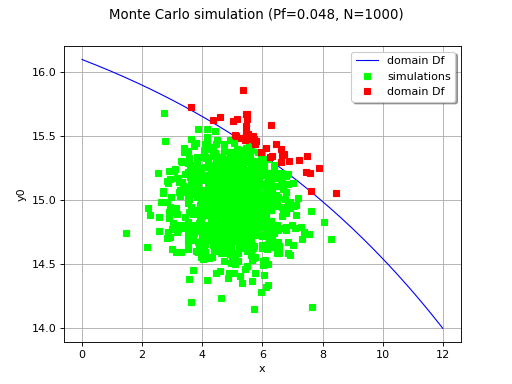
../../_images/monte_carlo_simulation-1.png

The method is also referred to as Direct sampling, Crude Monte Carlo method, Classical Monte Carlo integration.

API:

Examples:

References:

  • Robert C.P., Casella G. (2004). Monte-Carlo Statistical Methods, Springer, ISBN 0-387-21239-6, 2nd ed.

  • Rubinstein R.Y. (1981). Simulation and The Monte-Carlo methods, John Wiley & Sons