ReverseHaltonSequence

(Source code, png, hires.png, pdf)

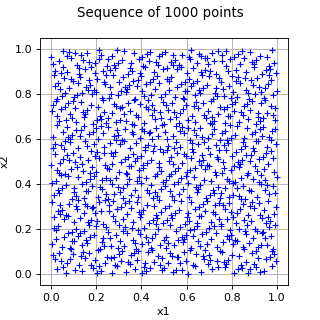
class ReverseHaltonSequence(*args)

Reverse Halton sequence.

Available constructors:

ReverseHaltonSequence(dimension=1)

Parameters

dimensionpositive int

Dimension of the points.

Examples

>>> import openturns as ot
>>> sequence = ot.ReverseHaltonSequence(2)
>>> print(sequence.generate(5))
0 : [ 0.5      0.666667 ]
1 : [ 0.25     0.333333 ]
2 : [ 0.75     0.222222 ]
3 : [ 0.125    0.888889 ]
4 : [ 0.625    0.555556 ]

Methods

ComputeStarDiscrepancy(sample)	Compute the star discrepancy of a sample uniformly distributed over [0, 1).
generate(*args)	Generate a sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).
getClassName()	Accessor to the object's name.
getDimension()	Accessor to the dimension of the points of the low discrepancy sequence.
getId()	Accessor to the object's id.
getName()	Accessor to the object's name.
getScramblingState()	Accessor to the linear congruential generator (LCG) used to scramble the sequences.
getShadowedId()	Accessor to the object's shadowed id.
getVisibility()	Accessor to the object's visibility state.
hasName()	Test if the object is named.
hasVisibleName()	Test if the object has a distinguishable name.
initialize(dimension)	Initialize the sequence.
setName(name)	Accessor to the object's name.
setScramblingState(state)	Accessor to the linear congruential generator (LCG) used to scramble the sequences.
setShadowedId(id)	Accessor to the object's shadowed id.
setVisibility(visible)	Accessor to the object's visibility state.

__init__(*args)

static ComputeStarDiscrepancy(sample)

Compute the star discrepancy of a sample uniformly distributed over [0, 1).

Parameters

sample2-d sequence of float

Returns

starDiscrepancyfloat

Star discrepancy of a sample uniformly distributed over [0, 1).

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> sample = sequence.generate(16)
>>> print(sequence.computeStarDiscrepancy(sample))
0.12890625
>>> sample = sequence.generate(64)
>>> print(sequence.computeStarDiscrepancy(sample))
0.0537109375

generate(*args)

Generate a sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).

Parameters

sizeint

Number of points to be generated. Default is 1.

Returns

sampleSample

Sample of pseudo-random vectors of numbers uniformly distributed over [0, 1).

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]

getClassName()

Accessor to the object’s name.

Returns

class_namestr

The object class name (object.__class__.__name__).

getDimension()

Accessor to the dimension of the points of the low discrepancy sequence.

Returns

dimensionint

Dimension of the points of the low discrepancy sequence.

getId()

Accessor to the object’s id.

Returns

idint

Internal unique identifier.

getName()

Accessor to the object’s name.

Returns

namestr

The name of the object.

getScramblingState()

Accessor to the linear congruential generator (LCG) used to scramble the sequences.

Returns

stateint

The state of the LCG, defined by the recursion .

getShadowedId()

Accessor to the object’s shadowed id.

Returns

idint

Internal unique identifier.

getVisibility()

Accessor to the object’s visibility state.

Returns

visiblebool

Visibility flag.

hasName()

Test if the object is named.

Returns

hasNamebool

True if the name is not empty.

hasVisibleName()

Test if the object has a distinguishable name.

Returns

hasVisibleNamebool

True if the name is not empty and not the default one.

initialize(dimension)

Initialize the sequence.

Parameters

dimensionint

Dimension of the points of the low discrepancy sequence.

Examples

>>> import openturns as ot
>>> # Create a sequence of 3 points of 2 dimensions
>>> sequence = ot.LowDiscrepancySequence(ot.SobolSequence(2))
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]
>>> print(sequence.generate(3))
0 : [ 0.375 0.375 ]
1 : [ 0.875 0.875 ]
2 : [ 0.625 0.125 ]
>>> sequence.initialize(2)
>>> print(sequence.generate(3))
0 : [ 0.5  0.5  ]
1 : [ 0.75 0.25 ]
2 : [ 0.25 0.75 ]

setName(name)

Accessor to the object’s name.

Parameters

namestr

The name of the object.

setScramblingState(state)

Accessor to the linear congruential generator (LCG) used to scramble the sequences.

Parameters

stateint

The state of the LCG, defined by the recursion .

setShadowedId(id)

Accessor to the object’s shadowed id.

Parameters

idint

Internal unique identifier.

setVisibility(visible)

Accessor to the object’s visibility state.

Parameters

visiblebool

Visibility flag.